Maths Notes for Chapter 2 Polynomials Class 10 - FREE PDF Download
Polynomials Class 10 Maths Chapter 2 CBSE Notes - 2025-26



FAQs on Polynomials Class 10 Maths Chapter 2 CBSE Notes - 2025-26
1. What are the most important concepts to revise in Polynomials Class 10 for quick exam preparation?
For effective revision of Polynomials Class 10, focus on these core concepts:
- Definition and types of polynomials (linear, quadratic, cubic)
- Degree of a polynomial and how to identify it
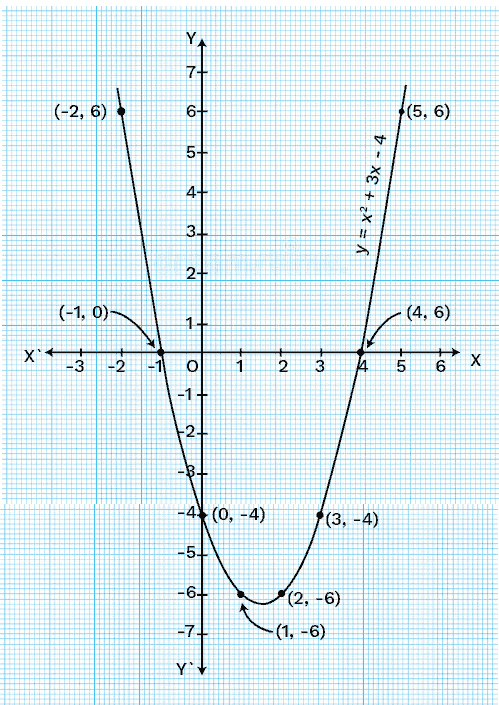
- Zeros of a polynomial and their graphical meaning
- The relationship between coefficients and zeroes for quadratic polynomials
- The Division Algorithm for polynomials and its application
2. How can students quickly identify the type of a polynomial and its degree during revision?
To identify the type and degree of a polynomial, look at the highest power of the variable:
- If the highest power is 1, it’s a linear polynomial.
- If it’s 2, it’s a quadratic polynomial.
- If it’s 3, it’s a cubic polynomial.
3. What is the significance of 'zeroes of a polynomial' in Class 10 revision notes?
Zeroes of a polynomial are the values of the variable for which the polynomial equals zero. For example, if p(x) = 0 at x = k, then k is a zero of the polynomial. These zeroes correspond to the points where the polynomial graph crosses the x-axis, and understanding them is key for solving equations and graph-based questions in exams.
4. Why is the Division Algorithm for polynomials important in Class 10 revision?
The Division Algorithm for polynomials allows you to express a polynomial as: Dividend = Divisor × Quotient + Remainder. This concept is crucial for factorizing polynomials, checking for factors, and simplifying expressions—all of which are essential for solving CBSE exam problems efficiently and accurately.
5. How should key polynomial formulas be revised for quick recall in exams?
For quick recall, create a revision sheet of essential polynomial formulas, such as:
- Sum of zeroes: α + β = -b/a
- Product of zeroes: αβ = c/a
- General division: Dividend = Divisor × Quotient + Remainder
6. How do topic connections in Polynomials help in faster revision for board exams?
Connecting related topics, like factorization, zeros, and the division algorithm, enables a smoother revision flow. By understanding how each concept builds on the previous one, you can recall information more efficiently during the exam and answer integrated questions confidently.
7. What common mistakes should students avoid when revising Polynomials in Class 10?
Common errors include:
- Misidentifying the degree by overlooking the highest power
- Confusing zeroes with factors
- Missing negative signs in formulas
- Forgetting to compare degrees in division problems
8. How can concept maps help in the quick revision of Polynomials Class 10 Notes?
Concept maps visually organize relationships between polynomial concepts, such as types, degree, factorization, and zeroes. They offer a bird’s-eye view of the chapter, making it easier to see topic interconnections and enabling faster, more structured revision before exams.




















 Watch Video
Watch Video




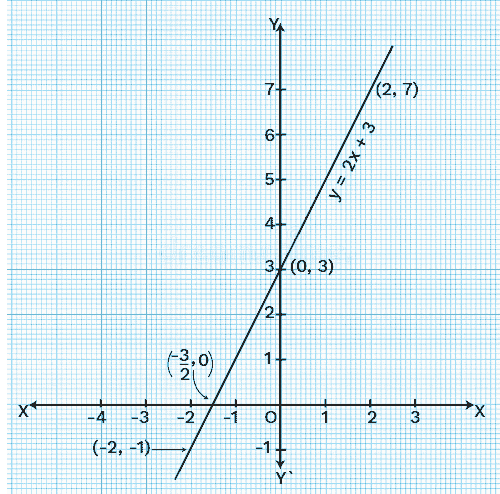
![The graph cuts \[\text{x-}\]axis at two distinct points \[\text{A}\]and \[\text{A }\!\!'\!\!\text{ }\]](https://www.vedantu.com/seo/content-images/0380daf6-a4f0-4033-8282-1de34df19e30.png)
![The graph cuts \[\text{x-}\]axis at two distinct points \[\text{A}\]and \[\text{A }\!\!'\!\!\text{ }\]](https://www.vedantu.com/seo/content-images/6376383b-5d4f-4b4b-80a4-0647b3ce8afa.png)
![The graph cuts the \[\text{x-}\]axis at exactly one point](https://www.vedantu.com/seo/content-images/a67baba1-1ff5-4702-bd38-ce6449198a5e.png)
![The graph cuts the \[\text{x-}\]axis at exactly one point](https://www.vedantu.com/seo/content-images/b06427b5-04aa-4d76-a7f6-5864941d830d.png)
![the graph is either completely above the \[\text{x-}\]axis or completely below the \[\text{x-}\]axis](https://www.vedantu.com/seo/content-images/d09d2a49-7d52-4f90-a995-fa4774936bad.png)
![the graph is either completely above the \[\text{x-}\]axis or completely below the \[\text{x-}\]axis](https://www.vedantu.com/seo/content-images/c813bd14-5408-4d20-bef4-1b6047c29661.png)
















