Class 11 Physics To Observe And Explain The Effect Of Heating On A Bimetallic Strip Experiment

Thermal Expansion - An Introduction

The expansion of an object on heating is called the thermal expansion of that object. This phenomenon can be observed in solids, liquids and gases. Thermal expansion is minimum in solids and maximum in gases because intermolecular forces are maximum in solids and minimum in gases. There are three types of thermal expansion of solids: Linear expansion, Area expansion and Volume expansion. In this article, we will study the effect of heating on a bimetallic strip.

Table of Contents:

• Aim

• Apparatus Required

• Theory

• Procedure

• Observations

• Result

• Precautions

• Lab Manual Questions

• Viva Questions

• Practical Based Questions

Aim

To observe and explain the effect of heating on a bimetallic strip.

Apparatus Required

• A iron-brass bimetallic strip with an insulating handle

• Heater or burner

Theory

A bimetallic strip is made of two strips of different metals but of the same dimensions. When we heat it uniformly, it tends to form an arc. The metal with a greater linear expansion coefficient lies on the convex side. In simple words, we can say that riveting two metal strips make a bimetallic strip of different materials and the same length. A bimetallic strip is generally used as a thermostat in electrical appliances like Geyser, Refrigerator, Fire alarms and Electric iron.

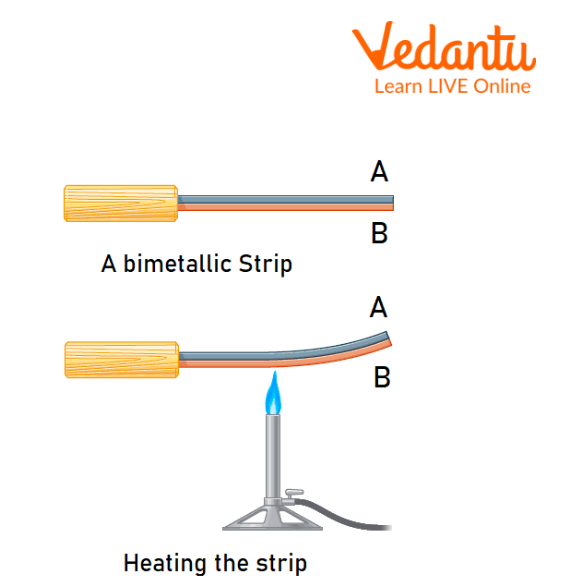
Bimetallic Strip In Straight And Bent Positions

As we can see from the figure, the bimetallic strip is straight at room temperature. When we heat it, both metallic pieces expand to different extents because of their different linear thermal expansivities and because of that, the bimetallic strip appears to bend.

When a solid is heated, it increases in thickness, length and breadth. The increase in length depends on the coefficient of linear thermal expansion, the original length and the temperature rise.

Consider a bimetallic strip of two different metals. Let ${L_1}$ be the length of a strip at temperature ${t_1}^\circ C$

Let ${L_2}$ be the length of a strip at ${t_2}^\circ C$

Here, consider that ${t_2}$ > ${t_1}$

The change in length ${L_2} - {L_1}$ is directly proportional to the original length ${L_1}$ and the rise in temperature ${t_2} - {t_1}$

So, ${L_2} - {L_1} = \alpha {L_1}\left( {{t_2} - {t_1}} \right)$

Therefore, ${L_2} = {L_1}[1 + \alpha \left( {{t_2} - {t_1}} \right)]$

and $\alpha  = \dfrac{{\left( {{L_2} - {L_1}} \right)}}{{\left( {{t_2} - {t_1}} \right)}}$ 

Where, $\alpha $ is the coefficient of linear thermal expansion of the metal of the strip. The SI unit of the coefficient of linear thermal expansion is ${K^{ - 1}}$

Procedure

• First of all, place the bimetallic strip on a horizontal surface to check whether the strip is straight or not in the beginning.

• Now, suspend the bimetallic strip in a clamp stand from its one end and light a burner. Heat the bimetallic strip with the help of a burner and observe the bending of the strip. 

• We need to note down which side of the bimetallic strip is in direct contact with the heat source.

• Now, observe the effect of heating the bimetallic strip and carefully note the direction of the bending of the free end of the bimetallic strip, whether it is upwards or downwards.

• Now, identify the metal on the convex side of the bimetallic strip and the one on its concave side. 

• We can observe that the one on the convex side of the bimetallic strip will expand more, and hence it will have larger linear thermal expansion.

• Now, note the temperature after each rise of temperature by 2 $^\circ C$ and the position of the upper edge at that temperature. 

• Record the observations as given below.

• Now, take the bimetallic strip away from the heat source and allow the bimetallic strip to cool to room temperature.

Observations

• Room temperature $\theta $ = _____ $^\circ C$

• Least Count Of Vernier Scale = $1mm$

Result

The bending of a bimetallic strip on heating is because of the difference in coefficient of linear expansion of the two metals of the strip and it is found from the experiment that bimetallic strip bends more and more as its temperature rises.

Precautions

• The two strips we use to perform this experiment should be firmly riveted near their ends. 

• One end of the bimetallic strip should be clamped rigidly, and the heating of the whole bimetallic strip should be uniform.

• The length of the bimetallic strip should be large as compared to its width or thickness.

Lab Manual Questions 

1. Suppose a bimetallic strip is made of brass and silver. Can we use this bimetallic strip in the thermostat?

Ans: This type of bimetallic strip can not be used in the thermostat because they have a negligible difference in thermal expansion properties. The thermostat is a device used to maintain a desired temperature in a system like an air-conditioner, refrigerator and electric iron. It works on the principle of thermal expansion of solid materials.

2. Why is mercury used in thermometers?

Ans: Mercury is a metal in a liquid state at room temperature. It is  used in thermometers because it has higher boiling and lower freezing points and expands on heating due to the high thermal coefficient of linear expansion. The other reason is that it does not stick to the glass tube and is a shining metal.

3. State one disadvantage of bimetallic strips.

Ans: There will be a change in the quality of metal if we use it regularly, which may lead to an error while measuring.

Viva Questions

1. Name one device which uses a bimetallic strip.

Ans: A fire alarm is a device which uses a bimetallic strip.

2. State two different types of bimetallic strips.

Ans: Spiral strip type and helical type are the two different types of bimetallic strips.

3. Can we use bimetallic strips in fans?

Ans: Yes, we can use bimetallic strips in fans to convert temperature into mechanical displacement.

4. State two advantages of the bimetallic thermometer.

Ans: The bimetallic thermometer can easily be installed, and wide temperature ranges are available. Another advantage is that its cost is meagre.

5. Define linear thermal expansion.

Ans: The change in length due to heat at constant pressure is known as linear thermal expansion.

6. Which device is used to measure the hotness or coldness of an object?

Ans: A thermometer is a device used to measure an object's hotness or coldness.

7. Give two applications of bimetallic strips.

Ans: Bimetallic strip is used in iron box, heat engines and in thermistors also.

8. Name one device which works on the principle of thermal expansion.

Ans: Bimetallic thermostat works on the principle of thermal expansion.

Practical Based Questions

1. We can measure temperature in

1. Second

2. Newton

3. Kelvin

4. Tesla

Ans: Option C - Kelvin

2. S.I. unit of heat is

1. Ampere

2. Joule

3. Tesla

4. Second

Ans: Option B - Joule

3. _____ should be filled in the bulb of a thermometer.

1. Lead

2. Silver

3. Gold

4. Mercury

Ans: Option D - Mercury

4. 1 cal = _____ joule

1. 9.9

2. 7.9

3. 4.2

4. 1.0

Ans: Option C - 4.2

5. We can measure heat by _____

1. Galvanometer

2. Thermometer

3. Calorimeter

4. None of the above

Ans: Option C - Calorimeter

6. Bimetallic strip is used in _____

1. Fire alarms

2. galvanometer

3. Ammeter

4. None of the above

Ans: Option A - Fire alarms

7. In solids, transfer of heat takes place by the process of _____

1. Radiation

2. Conduction

3. Convection

4. None of the above

Ans: Option B - Conduction

8. Bimetallic strip is made up of _____

1. Metals with different linear expansion coefficients

2. More than two metals with the same linear expansion coefficient

3. More than two metals with different lengths

4. None of the above

Ans: Option A - Metals with different linear expansion coefficient

9. Thermometer works on the _____

1. Faraday’s law of induction

2. Ampere’s circuital law

3. Principle of thermal expansion

4. Coulomb’s law

Ans: Option C - Principle of thermal expansion

10. A device which is used to measure temperature is called _____

1. Telescope

2. Galvanometer

3. Thermometer

4. Micrometer

Ans: Option C - Thermometer

Conclusion

We can conclude from this experiment that 

• With the increase in temperature the bimetallic strip bends more. Bimetallic strip bends due to the metal thermal expansion property. 

• When the temperature increases, the bimetallic strip expands towards the metal which has a lower value of temperature coefficient and when the temperature decreases, the bimetallic strip expands towards the metal which has a higher value of temperature coefficient.