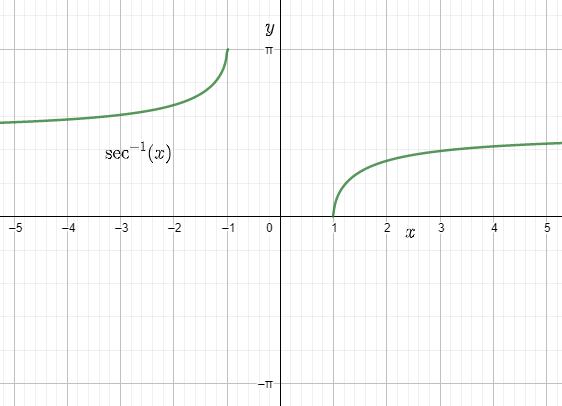Maths Notes for Chapter 2 Inverse Trigonometric Functions Class 12 - FREE PDF Download



FAQs on Inverse Trigonometric Functions Class 12 Maths Chapter 2 CBSE Notes - 2025-26
1. How do revision notes for Inverse Trigonometric Functions Class 12 help students master key concepts quickly?
Revision notes provide succinct summaries of definitions, properties, and formulas related to inverse trigonometric functions. By organising the material into clear sections—such as domains, ranges, principal values, and graphs—these notes make it easier for students to review major concepts and reinforce understanding in less time, supporting effective last-minute revision aligned with CBSE 2025–26 requirements.
2. What is the recommended sequence for revising the chapter on Inverse Trigonometric Functions in Class 12 Maths?
Begin with the basics of trigonometric functions and their domains and ranges. Next, study the definition of inverse trigonometric functions and focus on the principal value branches. Move on to learn key properties, standard formulas, and related graphs. End by practising property-based and mixed-concept questions to consolidate understanding before the exam.
3. Why is understanding the principal value branch crucial in inverse trigonometric functions?
The principal value branch ensures that every inverse trigonometric function yields a single, well-defined output for a given input. This prevents ambiguity in answers by restricting possible solutions to a standardised interval, which is essential for scoring accuracy in CBSE board exams and for solving equations without error.
4. How do the properties of inverse trigonometric functions simplify complex problems during revision?
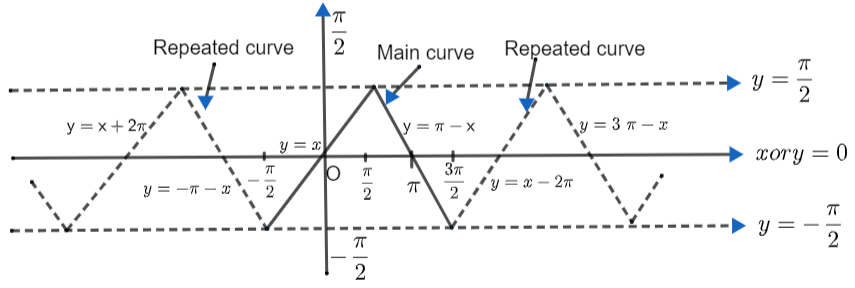
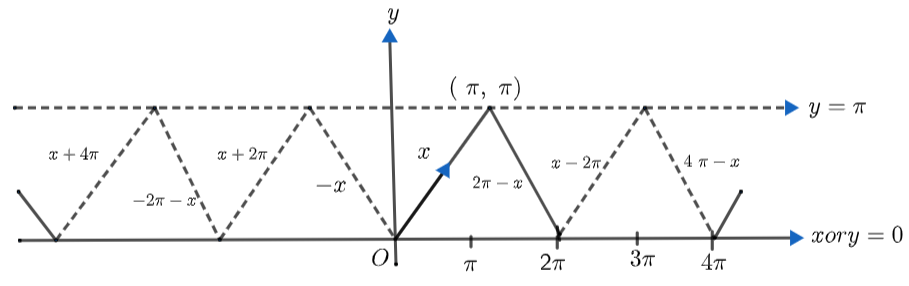
Properties such as odd/even behaviour, addition and subtraction formulas, and identities like sin–1(x) + cos–1(x) = π/2 allow students to convert complicated expressions into simpler forms. Using these properties can greatly reduce calculation steps and help tackle mixed-concept problems quickly, making revision more efficient and effective.
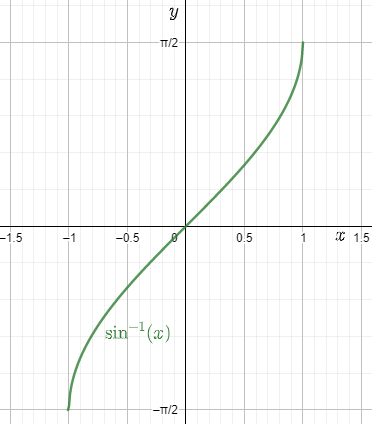
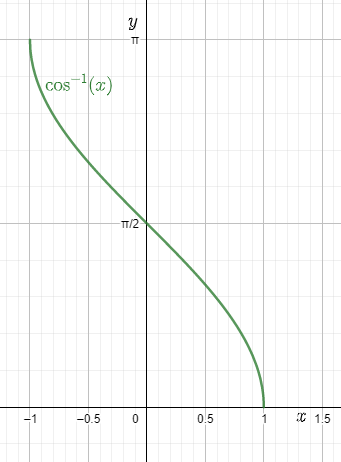
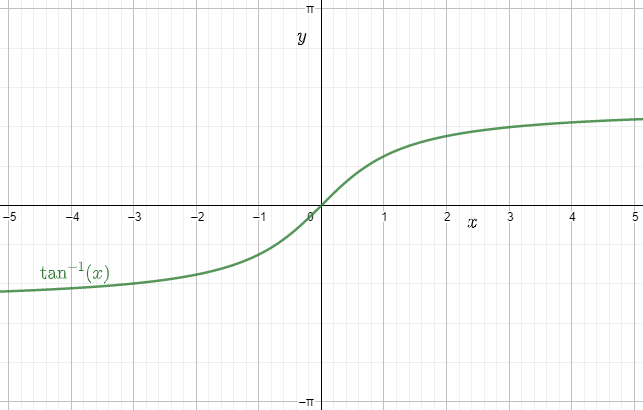
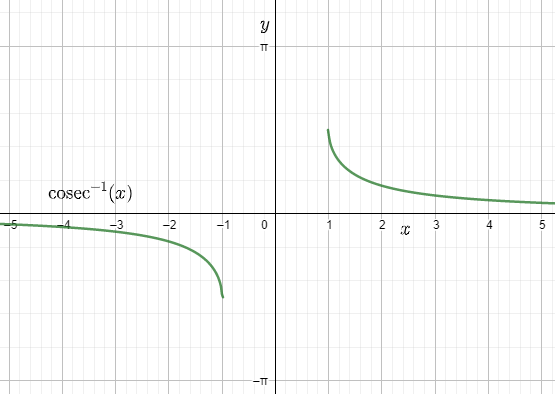
5. What are the standard domains and ranges students should memorise for each inverse trigonometric function?
- sin–1x: domain [–1, 1], range [–π/2, π/2]
- cos–1x: domain [–1, 1], range [0, π]
- tan–1x: domain (–∞, ∞), range (–π/2, π/2)
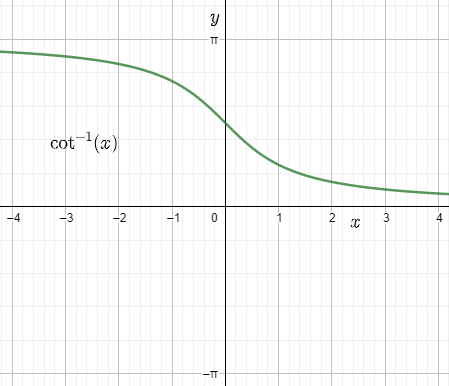
- cot–1x: domain (–∞, ∞), range (0, π)
- sec–1x: domain (–∞, –1] ∪ [1, ∞), range [0, π] (except π/2)
- cosec–1x: domain (–∞, –1] ∪ [1, ∞), range [–π/2, π/2] (except 0)
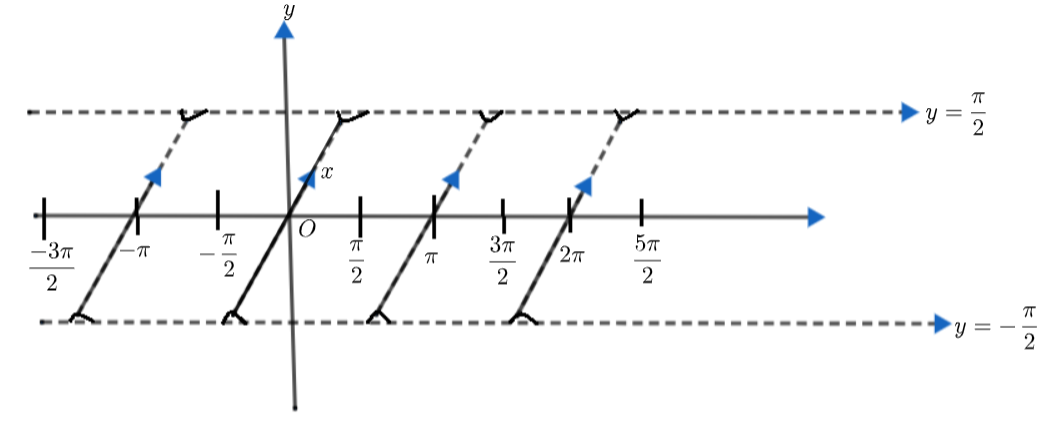
6. How do graphs of inverse trigonometric functions support better understanding during quick revision?
Graphs visually display the domain, range, monotonicity, and key turning points of each inverse function. By studying these, students can quickly identify where each function is increasing or decreasing, spot principal branches, and verify answers graphically—facilitating faster and more reliable solutions during exams.
7. What common pitfalls should students avoid when revising inverse trigonometric functions for CBSE exams?
Students often confuse domains and ranges, apply incorrect principal value intervals, or misuse addition/subtraction formulas. Avoid these mistakes by paying special attention to property lists in revision notes, double-checking ranges for each function, and practising worked examples provided in the notes to reinforce correct application.
8. How are the properties of inverse trigonometric functions interconnected with other chapters in Class 12 Maths?
Inverse trigonometric properties frequently appear in calculus chapters (integration and differentiation) and in solving equations involving multiple mathematical concepts. Strong grasp of these properties enables students to transition seamlessly between chapters and apply inverse trigonometric identities in broader mathematical contexts, enhancing problem-solving skills overall.
9. What revision techniques are most effective for memorising formulas and properties from the chapter?
- Create summary sheets featuring all major formulas and properties
- Practice derivations of key properties (e.g., even/odd function behaviours)
- Solve varied examples based on each property
- Group similar identities to spot patterns
- Review summary charts before tests for quick recall
10. How do revision notes ensure full alignment with the latest CBSE 2025–26 Maths syllabus for Inverse Trigonometric Functions?
Revision notes follow the official CBSE topic order, covering compulsory properties, proofs, standard graphs, and applications stated in the syllabus. They emphasise recent exam trends, include higher-order problem types, and clearly mark sections based on areas the board highlights as important—ensuring students revise exactly what is required for exam success.
11. Why is the understanding of odd and even properties of inverse trigonometric functions essential during revision?
Recognising which inverse functions are odd or even helps in simplifying expressions such as sin–1(–x) = –sin–1(x) and tan–1(–x) = –tan–1x. This knowledge allows for quick identification of answer signs and reduces errors in competitive and board exams.
12. How can understanding the proofs and logical steps behind properties help beyond rote memorisation?
Grasping the logical reasoning behind each property gives deeper insight into why a property holds, supporting flexibility when tackling unfamiliar problems. It also boosts confidence in derivations, minimises mistakes due to rote errors, and prepares students for higher-order CBSE 2025–26 exam questions that test application instead of memorisation alone.
13. What role do summary charts and revision maps play in quick last-minute preparation for Inverse Trigonometric Functions?
Summary charts and revision maps bring together all formulas, domains, ranges, and key properties in one place for fast reference. This accelerates revision by minimising page-flipping and helps ensure no important concept is left out when preparing for the CBSE Class 12 Maths exam’s Inverse Trigonometric Functions chapter.
14. How can mastering inverse trigonometric function properties help in solving integrals and equations in calculus?
A solid command of inverse trigonometric identities allows students to transform complex integrals or equations into standard forms that are easier to integrate or solve. These properties often provide the necessary substitutions and simplifications for efficient calculation in calculus problems across the Class 12 syllabus.
15. What makes a revision note ‘effective’ for the Inverse Trigonometric Functions chapter in board exam prep?
An effective revision note is concise, clearly highlights key formulas and proofs, organises properties by function, offers illustrative graphs, and uses solved examples to connect concepts. It aligns fully with the latest CBSE 2025–26 syllabus and is designed for step-wise revision, making even the most challenging concepts accessible for board-level mastery.