Physics Notes for Chapter 14 Waves Class 11 - FREE PDF Download
FAQs on Waves Class 11 Physics Chapter 14 CBSE Notes - 2025-26
1. What key concepts should I focus on while revising Class 11 Physics Chapter 14 – Waves?
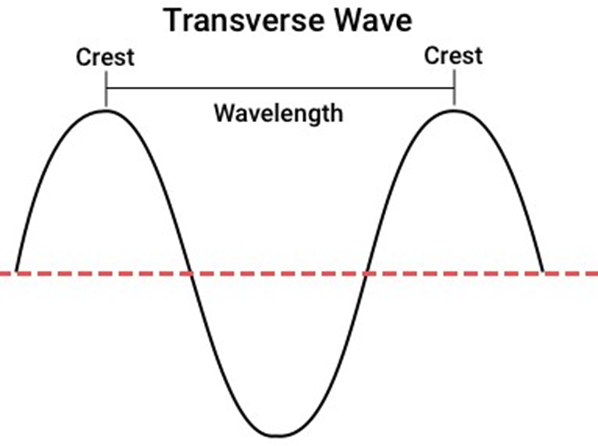
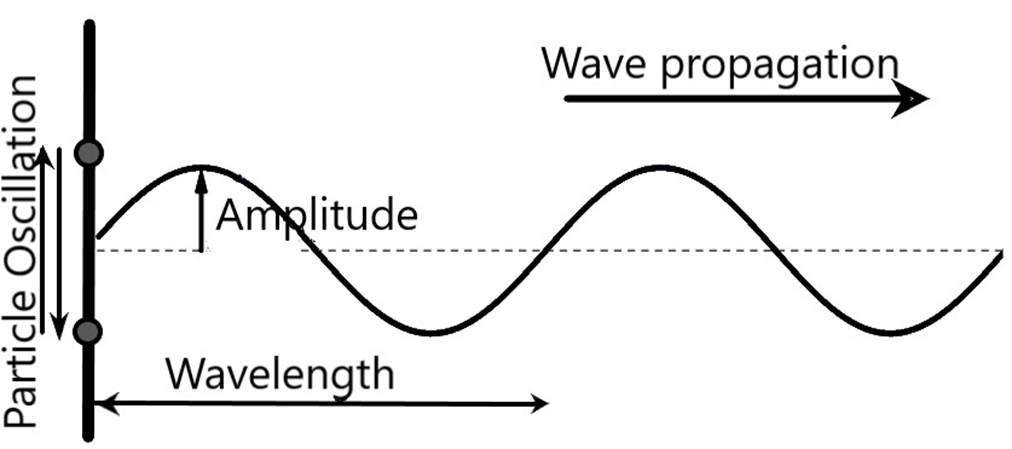
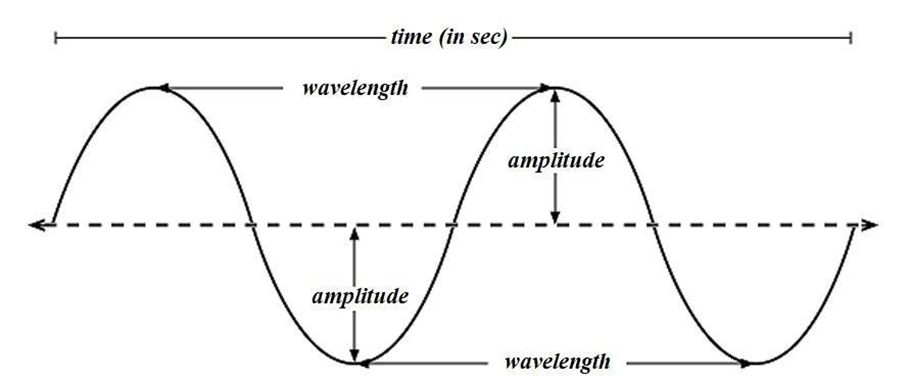
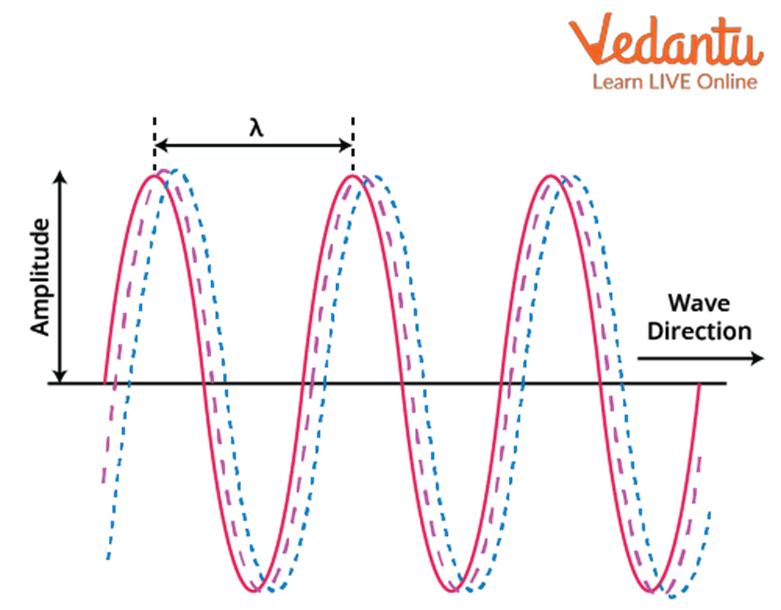
While revising Waves Class 11, concentrate on understanding types of waves (transverse and longitudinal), displacement relations in progressive waves, wave speed and its formula, principle of superposition, and reflection and formation of standing waves. Ensure you also grasp key terms like amplitude, frequency, wavelength, phase, and nodes/antinodes.
2. How can I quickly recall the difference between transverse and longitudinal waves for revision?
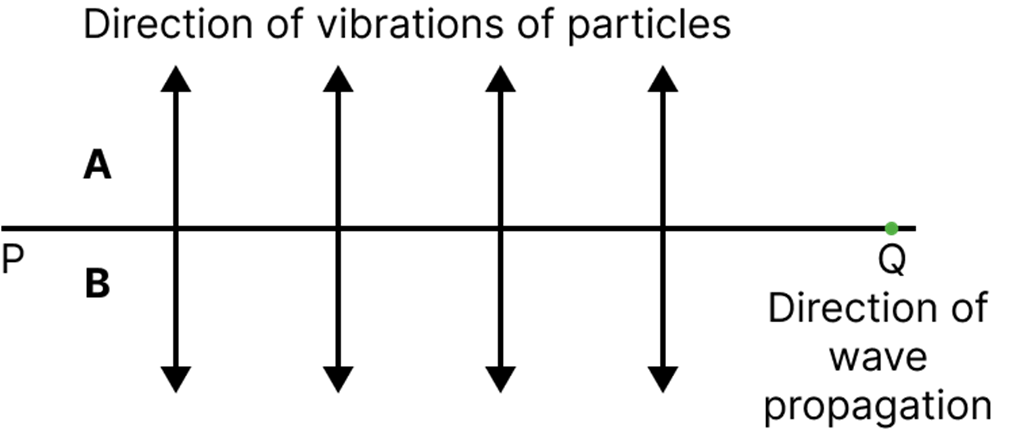
Transverse waves have particle motion perpendicular to the direction of propagation (e.g. light waves, waves on a string), while longitudinal waves have particle motion parallel (e.g. sound waves). Remember: transverse = crests/troughs, longitudinal = compressions/rarefactions.
3. What are the main formulas to revise for Chapter 14 Waves in Class 11 Physics?
- Wave speed: v = fλ
- Wavelength relation: λ = v/f
- Period: T = 1/f
- Displacement (progressive wave): y(x, t) = A sin(kx - ωt + φ)
- Speed on stretched string: v = √(T/μ)
4. What is the principle of superposition of waves, and why is it important for revision?
The principle of superposition states that when two or more waves overlap, the resultant displacement at any point is the algebraic sum of their individual displacements. This concept is fundamental for understanding interference, beats, and standing waves, all of which are frequent exam topics.
5. How can I structure my revision for Chapter 14 to maximize recall?
- Start with definitions and classifications of waves.
- Move to mathematical relations and key formulas.
- Practice solved examples involving calculation of speed, frequency, period, and displacement.
- Review applications such as sound waves, beats, the Doppler effect, and wave reflection.
- Summarize key differences (e.g., between wave types and standing vs progressive waves).
6. Why do standing waves form, and what is their significance in Physics?
Standing waves form when two identical waves travelling in opposite directions interfere, resulting in points of no displacement (nodes) and maximum displacement (antinodes). They are significant for explaining phenomena in musical instruments and resonance cavities, and help in understanding energy distribution in confined systems.
7. How can understanding wave characteristics help in solving real-world problems?
Knowledge of wave speed, frequency, amplitude, and wavelength allows you to explain and predict the behavior of sound, light, and water waves in various scenarios. For example, you can compute the speed of sound in air, determine resonance in musical instruments, or analyze seismic waves in earthquake studies.
8. What are some common misconceptions students should avoid during last-minute revision of Waves?
- Confusing direction of particle motion in transverse vs longitudinal waves.
- Assuming all waves require a medium – electromagnetic waves do not.
- Mixing up wave speed with the speed of particles in the medium.
- Ignoring phase difference when analyzing interference/superposition questions.
9. How are the concepts of amplitude and phase relevant for Class 11 Board Exams?
Amplitude measures maximum displacement and is linked to energy in a wave. Phase describes the current state within the cycle and affects how waves interfere. Both are essential for solving problems on wave motion, superposition, and standing waves, which are frequently asked in exams.
10. Which strategies will help me revise and retain the formulas from Waves Class 11 Notes?
- Create a concept map linking all wave properties and formulas.
- Regularly practice formula-based numerical problems.
- Recite important equations and their physical meaning aloud.
- Summarize formulas on a single sheet for quick last-minute revision.
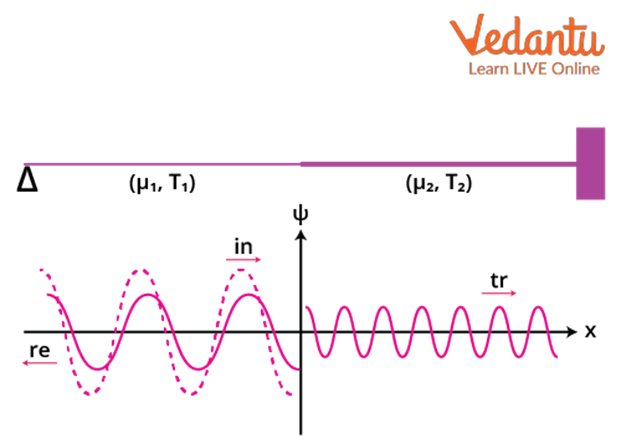
11. How does the reflection of waves occur and what key points should I remember for exams?
Wave reflection happens when a wave hits a boundary and bounces back. With a fixed end, the wave inverts; with a free end, it does not. Remember that nodes and antinodes can form due to interference between incident and reflected waves.
12. Can you explain the importance of practising wave-related numericals for quick revision?
Solving numerical problems on wave speed, wavelength, frequency, and standing waves enhances conceptual clarity, improves recall of formulas, and prepares you for the variety of questions in CBSE exams, where application is often tested alongside theory.
13. What summary tips would you give for a last-minute revision of Chapter 14 Waves?
- Revise definitions, types, and essential formulas.
- Review solved sample problems for each subtopic.
- Summarize key differences and applications.
- Check for common mistakes, especially with units and graph interpretation.
- Utilize concept maps and flashcards for fast recall.