Kinetic Theory Class 11 Notes: CBSE Physics Chapter 12

What is Kinetic Theory?

• The kinetic theory of gases describes how gases behave by assuming that the gas is made up of quickly moving atoms or molecules. 

• Because there is no intermolecular space in solids, molecules are incredibly densely packed. Intermolecular gaps are larger in liquids than in solids, and molecules in gases are loosely packed due to the huge intermolecular spaces. 

• The kinetic theory of gases explains the random movement of molecules in a gas.

• We'll also look at why kinetic theory is considered a successful theory.

• The following things are explained by the Kinetic theory:

• Pressure and temperature interpretation at the molecular level can be described.

• It's in line with Avogadro's theory and gas laws. 

• Explains the specific heat capacity of a variety of gases correctly.

Molecular Nature of Matter

• Many scientists have proposed the atomic hypothesis. According to this theory, atoms make up everything in the universe. 

• Atoms are tiny particles that move around in a constant order, attracting one another when they are close enough. When they are forced to be very close to each other, however, they repel each other.

• The atomic theory of Dalton is also known as the molecular theory of matter. This theory establishes that matter is composed of molecules, which are composed of atoms.

• When gases combine chemically to form another gas, their volumes are in small integer ratios, according to Gay Lussac's law.

• According to Avogadro's law, all gases have the same number of molecules in equal volumes at the same temperature and pressure.

• Conclusion: All of these principles demonstrate the molecular nature of gases.

• Kinetic theory is based on Dalton's molecular theory.

Why was Dalton’s Theory a Success?

• Molecules are made up of atoms, which are built up of molecules.

• An electron microscope can examine atomic structure.

Solids, Liquids and Gases in Terms of Molecular Structure

Behaviour of Gases

• Gases at low pressures and temperatures much higher than those at which they liquify (or solidify) approximate a relationship between pressure, temperature, and volume.

\[{\text{PV}} = {\text{KT}}\] ...........(1)

This is the universal relationship that all gases satisfy.

where P, V, and T denote pressure, volume, and temperature, and K denotes the constant for a given volume of gas. It fluctuates depending on the amount of gas present.

${\text{K}} = {\text{N}}{{\text{k}}_{\text{B}}}$ , where N is the number of molecules, ${{\text{K}}_{\text{B}}}$ is the Boltzmann constant whose value never changes.

• From equation (1), 

${\text{PV}} = {\text{N}}{{\text{k}}_{\text{B}}}{\text{T}}$ 

• Therefore, $\dfrac{{{\text{PV}}}}{{{\text{NT}}}} = {{\text{k}}_{\text{B}}}$ , this will be same for all gases. 

• Two gases having pressure, temperature and volume as (P1, T1, V1) and (P2, T2, V2) are considered. 

• Therefore, $\dfrac{{{{\text{P}}_{\text{1}}}{{\text{V}}_{\text{1}}}}}{{{{\text{N}}_{\text{1}}}{{\text{T}}_{\text{1}}}}} = \dfrac{{{{\text{P}}_{\text{2}}}{{\text{V}}_{\text{2}}}}}{{{{\text{N}}_{\text{2}}}{{\text{T}}_{\text{2}}}}}$ 

• The conclusion for the above relation is that it is satisfied by all gases at high temperatures and low pressures.

Justification of Avogadro’s Hypothesis from the Equation of Gas

• According to Avogadro's hypothesis, all gases have the same number of molecules in equal volumes at the same temperature and pressure.

• Consider the equation $\dfrac{{{\text{PV}}}}{{{\text{NT}}}}$ = constant: if P, V, and T are the same for two gases, then N (number of molecules) will be the same as well.

• At constant P and T, Avogadro's hypothesis states that the number of molecules per unit volume is the same for all gases.

• NA stands for Avogadro number. Where NA is equal to $6.02 \times {10^{23}}$. It has universal significance.

• At standard temperature and pressure, the mass of 24.4 litres of any gas equals the molecular weight in grams, according to experiments.

Perfect Gas Equation

• A perfect gas equation is given by the following formula: ${\text{PV}} = \mu {\text{RT}}$ , where P is pressure, V is the volume, T is the absolute temperature, $\mu $ is the number of moles and R is the universal gas constant. 

${\text{R}} = {{\text{k}}_{\text{B}}}{{\text{N}}_{\text{A}}}$ , where ${{\text{k}}_{\text{B}}}$ is the Boltzmann constant and ${{\text{N}}_{\text{A}}}$ is the Avogadro’s number.

• This equation describes how gas behaves in a specific condition.

• If a gas fulfils this equation, it is referred to as a perfect gas or an ideal gas.

Different Forms of Perfect Gas Equation

1. ${\text{PV}} = \mu {\text{RT}}$, where $\mu $ is number of moles; $\mu  = \dfrac{{\text{N}}}{{{{\text{N}}_{\text{A}}}}}$ , N is the number of molecules and NA is the Avogadro number.

Now, ${\text{PV}} = \dfrac{{\text{N}}}{{{{\text{N}}_{\text{A}}}}}{\text{RT}}$ 

After simplification, ${\text{PV}} = {\text{N}}{{\text{k}}_{\text{B}}}{\text{T}}$ 

${\text{P}} = \dfrac{{\text{N}}}{{\text{V}}}{{\text{k}}_{\text{B}}}{\text{T}}$ , where ${\text{n}} = \dfrac{{\text{N}}}{{\text{V}}}$ 

So, ${\text{P}} = {\text{n}}{{\text{k}}_{\text{B}}}{\text{T}}$, where n is the number of density

2. Also, $\mu  = \dfrac{{\text{M}}}{{{{\text{M}}_ \circ }}}$ , where M is the mass of the sample and Mo is the molar mass of the sample. 

So, ${\text{PV}} = \dfrac{{\text{M}}}{{{{\text{M}}_ \circ }}}{\text{RT}}$

${\text{P}} = \dfrac{{\text{M}}}{{\text{V}}}\dfrac{{{\text{RT}}}}{{{{\text{M}}_ \circ }}}$ 

${\text{P}} = \rho \dfrac{{{\text{RT}}}}{{{{\text{M}}_ \circ }}}$ , where $\rho $ is the mass density of the gas. $\rho  = \dfrac{{\text{M}}}{{\text{V}}}$ 

Ideal Gas

• At all pressures and temperatures, a gas exactly fulfils the perfect gas equation. 

• The concept of an ideal gas is purely theoretical.

• There is no such thing as an ideal gas. The term "real gas" refers to an ideal gas.

• For low pressures and high temperatures, real gases approach ideal gas behaviour.

Real Gases Deviation from Ideal Gas

• For low pressures and high temperatures, real gases approach ideal gas behaviour.

• According to the ideal gas equation: ${\text{PV}} = \mu {\text{RT}}$, $\dfrac{{{\text{PV}}}}{{{\text{RT}}}}$ = constant. So, for an ideal gas, the graph should be a straight line (parallel to the x-axis). This means it has the same value regardless of temperature or pressure.

• However, at high temperatures and low pressures, the graph of real gases approaches ideal gas behaviour. 

• Molecules are far apart at high temperatures and low pressures. When the temperature is raised, the molecules will randomly move away from one another.

• As a result of the reduced molecule interaction, the gas acts like an ideal gas. When the molecular constituents of the gas do not interact with one another, the optimum behaviour emerges.

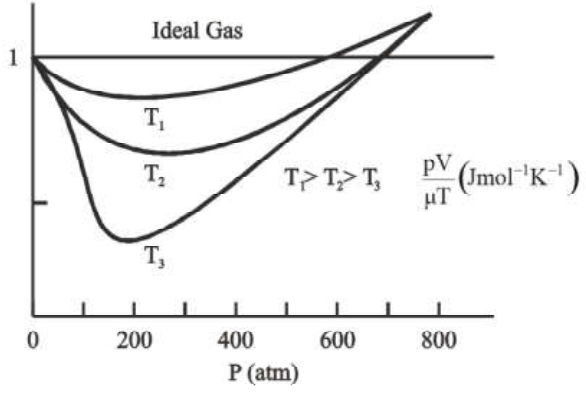
Real Gas Approaches Ideal Gas Behaviour at Low Pressures and High Temperatures

In the above graph it is shown that at low pressures and high temperatures, real gases approach the ideal gas behaviour.

Deduction of Boyle’s Law and Charles Law from Perfect Gas Equation

• Boyle’s Law: Boyle’s law is derived from the perfect gas equation, ${\text{PV}} = \mu {\text{RT}}$. The T is the temperature and $\mu $ is the number of moles and both of these values are considered constant.

Therefore, PV = constant. So, at a constant temperature, the pressure of a given mass of gas varies inversely with volume, according to Boyle's law.

• Charles’s Law: Here the pressure (P) is considered as constant. The according to the ideal gas equation, ${\text{PV}} = \mu {\text{RT}}$

$\dfrac{{\text{V}}}{{\text{T}}} = \dfrac{{\mu {\text{R}}}}{{\text{P}}}$ = constant

Therefore, $\dfrac{{\text{V}}}{{\text{T}}}$ = Constant

Hence, according to Charles’s law, at constant pressure, the volume of a gas is directly proportional to its absolute temperature. 

Therefore, it is concluded that Boyle’s Law and Charles’s Law are satisfied by the Ideal gas.

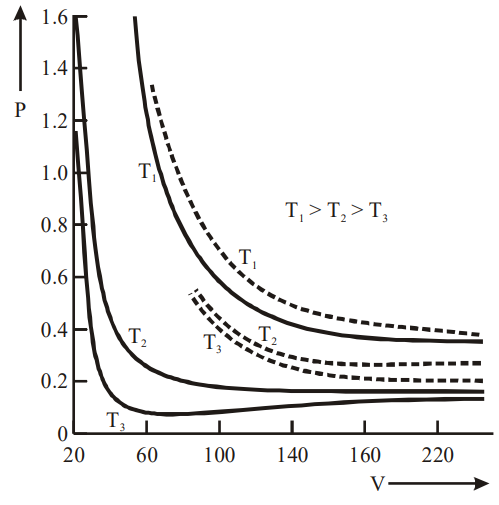
P-V Curve (solid lines)

The above graph depicts an experimental P-V curve (solid lines) for steam at three temperatures compared with Boyle’s law (dotted line).

Deducing Dalton’s Law of Partial Pressures

• The overall pressure of a mixture of ideal gases is equal to the sum of partial pressures, according to Dalton's partial pressure equation.

• If a vessel contains many ideal gases mixed, the total pressure of the vessel equals the sum of partial pressures. 

• The pressure imposed by a specific gas if just that gas is present in the vessel is known as partial pressure.

• Consider the following: - Consider a vessel containing a mixture of three gases, A, B, and C. As a result, the partial pressure of A equals the pressure applied just by A, assuming B and C are absent. Similarly, when A and C are absent, the partial pressure of B is equal to the pressure applied just by B. Similarly, the total pressure of the mixture is equal to the sum of the partial pressures of A, B, and C, according to Dalton's law.

To Show How the Perfect Gas Equation Concludes Dalton’s Law of Partial Pressure

• Assume you have a combination of ideal gases, which implies they don't interact with one another. \[{\text{PV}} = \mu {\text{RT}}\]  is the ideal gas equation.

Where P is the pressure, V is the volume, T is the absolute temperature and $\mu $ is the number of moles.

If the mixture of gases is present, then: $\mu  = {\mu _1} + {\mu _2} + ......$ so on.

Therefore, \[{\text{PV}} = ({\mu _1}{\text{ + }}{\mu _2}{\text{ + }}....{\text{)RT}}\]

${\text{P}} = ({\mu _1} + {\mu _2} + ...)\dfrac{{{\text{RT}}}}{{\text{V}}}$ 

${\text{P}} = \dfrac{{{\mu _1}{\text{RT}}}}{{\text{V}}} + \dfrac{{{\mu _2}{\text{RT}}}}{{\text{V}}} + ....$ 

Therefore, ${\text{P}} = {{\text{P}}_1} + {{\text{P}}_2} + ...$ 

Where P1 and P2 are the partial pressures of gas 1 and gas 2 respectively.

The overall pressure caused by a gas mixture is the sum of the partial pressures of the gases.

Kinetic Theory of an Ideal Gas

Basis of Kinetic Theory

(i) Gas molecules are in a constant state of random motion, interacting with one another and the container's walls.

(ii) Every collision is elastic.

(iii) Kinetic energy is conserved in total.

(iv) The total momentum of the system is conserved.

(v) The total Kinetic energy and momentum before the collision is identical to the total Kinetic energy and momentum after the collision in the event of an elastic collision.

What Does Kinetic Energy Tell?

(i) The molecule size is very small in comparison to the intermolecular distance between them under normal temperature and pressure.

(ii) In the case of a gas, molecules are very far apart, and their sizes are modest in comparison to the distance between them.

(iii) As a result, there is very little interaction between them. There will be no force between the molecules because there is no interaction between them.

(iv) As a result, molecules are free to move according to Newton's first law of motion.

(v) The molecules should move in a straight path, but as they get closer together, they encounter intermolecular interactions, which cause their velocities to alter.

(vi) Collision is the term for this phenomenon. These are elastic collisions.

The Pressure of an Ideal Gas Based on Kinetic Theory

Assumptions

• Consider a container in the shape of a cube that is filled with an ideal gas. Only one molecule will be considered; the molecule collides with the container's walls and bounces back.

• Let the molecule's velocity while moving be (vx, vy, vz).

• The velocity of the molecule as it bounces back will be (-vx, vy, vz).

• The change in momentum = Pf – Pi where Pf = final momentum and Pi = initial momentum)

• \[{{\text{P}}_{\text{f}}}-{\text{ }}{{\text{P}}_{\text{i}}} = {\text{ }} - {\text{m}}{{\text{v}}_{\text{x}}} - {\text{m}}{{\text{v}}_{\text{x}}} =  - 2{\text{m}}{{\text{v}}_{\text{x}}}\] 

• The wall receives this change in momentum as a result of the contact.

• One molecule's momentum delivered to the wall in a collision= 2mvx

However, because there are so many molecules, we must calculate the overall momentum transferred to the wall by them all.

To figure out how many molecules hit the wall, do the following:

The area of the wall will be ‘A’. Therefore, in time $\Delta t$ within a distance of $A{v_x}\Delta t$ all the molecules can hit the wall.

On average, half of the molecules will hit the wall and half of them will move away from the wall. Therefore, $(\dfrac{1}{2})A{v_x}\Delta t$ will hit the wall.

• The total momentum will be: ${\text{2m}}{{\text{v}}_{\text{x}}} \times \dfrac{1}{2}{\text{nA}}{{\text{v}}_{\text{x}}} \Delta t = {\text{An}}{{\text{v}}^{\text{2}}}_{\text{x}} \Delta tm$ 

• The force exerted on the wall is equal to the rate of change of momentum which will be equal to ${\text{An}}{{\text{v}}_{\text{x}}}^{\text{2}}{\text{m}}$ .

• The pressure on the wall is equal to: ${\text{P}} = \dfrac{{\text{F}}}{{\text{A}}} = {\text{nm}}{{\text{v}}_{\text{x}}}^{\text{2}}$ 

• Therefore, the value of pressure ${\text{P}} = {\text{nm}}{{\text{v}}_{\text{x}}}^{\text{2}}$ is true for the molecules having the velocity as vx.

Note:

• The velocity of all the molecules in the gas will not be the same. The velocities of each will be different.

• As a result, the following equation is valid for pressure due to a group of molecules moving at vx in the x-direction, where n is the number density of that group of molecules.

As a result, the total pressure owing to all such groups may be calculated by adding the contributions due to each molecule. $P = nm\overline {{v_x}^2} $.

• Because the gas is isotropic, the molecules travel at random, meaning that their velocity can be in any direction.

$\overline {{v_x}^2}  = \overline {{v_y}^2}  = \overline {{v_z}^2}  = \dfrac{1}{3}(\overline {{v_x}^2}  = \overline {{v_y}^2}  = \overline {{v_z}^2} ) = \dfrac{1}{3}{v^2}$ 

• Therefore, the pressure is equal to, ${\text{P}} = \dfrac{1}{3}{\text{nm}}{{\text{v}}^2}$ , where ${{\text{v}}^{\text{2}}}$ is the average square speed.

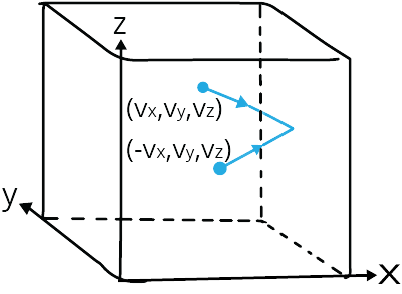
Elastic Collision of a Gas Molecule

The above image depicts an elastic collision of a gas molecule with the wall of the container.

Justifying the Assumptions

• The container carrying the gas is supposed to be a cube. The container's form is unimportant.

• We can establish the preceding derivation for a vessel of any arbitrary shape by selecting a small infinitesimal (planar) area.

• In the end, we will notice that the area and the change in time are absent.

• According to Pascal's law, the pressure in one region of a gas that is in equilibrium is the same as it is everywhere else.

• Collisions are not taken into account.

• With random collisions and a constant condition of gas, the number of molecules impacting the wall in time was found to equal $(\dfrac{1}{2})A{v_x}\Delta t$ .

• As a result, if a molecule with velocity (vx, vy, vz) obtains a different velocity as a result of colliding with other molecules, there will always be another molecule with a different initial velocity that acquires the velocity after the collision (vx, vy, vz).

• When molecular collisions are not frequent and the time spent in the collision is modest relative to the period between collisions, the above calculation is unaffected.

Kinetic Interpretation of Temperature

• A molecule's average kinetic energy is proportional to the absolute temperature of the gas.

• It is unaffected by the ideal gas's pressure, volume, or nature.

• For the equation: ${\text{P}} = \dfrac{1}{3}{\text{nm}}{{\text{v}}^2}$, multiply both the sides by V:

${\text{PV}} = \dfrac{1}{3}{\text{nVm}}{{\text{v}}^2}$

After simplifying the above equation:

${\text{PV}} = \dfrac{2}{3}{\text{N}} \times \dfrac{1}{3}{\text{m}}{{\text{v}}^2}$, where ${\text{n}} = \dfrac{{\text{N}}}{{\text{V}}}$ 

‘N’ is the number of molecules in a sample.

• Therefore, ${\text{PV}} = \dfrac{2}{3}{\text{E}}$ ....equation (1)

Where E is the kinetic energy which is equal to ${\text{E}} = \dfrac{1}{2}{\text{m}}{{\text{v}}^2}$ 

This is the foundation of kinetic temperature interpretation. 

• On combining the above-marked equation (1) with the ideal gas equation:

${\text{E}} = \dfrac{3}{2}{{\text{k}}_{\text{B}}}{\text{NT}}$ ......equation (2)

$\dfrac{{\text{E}}}{{\text{N}}} = \dfrac{1}{2}{\text{m}}{{\text{v}}^2} = \dfrac{3}{2}{{\text{k}}_{\text{B}}}{\text{T}}$ ......equation (3)

Therefore, the above equation depicts the average kinetic energy.

So, kinetic energy is directly proportional to the temperature. So, temperature can be identified as a molecular quantity.

Kinetic Theory: Consistent With Ideal Gas Equation and Gas Laws

1. It is consistent with the ideal gas equation:

For the kinetic gas equation:

$\dfrac{{\text{E}}}{{\text{N}}} = \dfrac{3}{2}{{\text{k}}_{\text{B}}}{\text{T}}$

${\text{E}} = \dfrac{3}{2}{\text{N}}{{\text{k}}_{\text{B}}}{\text{T}}$ 

For an ideal gas, its internal energy is directly proportional to the temperature. This depicts that the internal energy of an ideal gas is only dependent on its temperature, not on pressure or volume.

2. When Kinetic theory is consistent with Dalton’s law of partial pressure:

The equation for kinetic theory: ${\text{P}} = \dfrac{1}{3}{\text{nm}}{{\text{v}}^2}$ 

If a mixture of gases is present in the vessel, then:

${\text{P}} = \dfrac{1}{3}[{{\text{n}}_1}{{\text{m}}_1}{{\text{v}}_1}^2 + {{\text{n}}_2}{{\text{m}}_2}{{\text{v}}_2}^2 + ...]$ 

The average kinetic energy of molecules of different gases at equilibrium will be equal

$\dfrac{1}{2}{{\text{m}}_{\text{1}}}{{\text{v}}_1}^2 = \dfrac{1}{2}{{\text{m}}_{\text{2}}}{{\text{v}}_2}^2 = \dfrac{3}{2}{{\text{k}}_{\text{B}}}{\text{T}}$ 

 Then the total pressure will be: 

${\text{P}} = \dfrac{1}{3}[\dfrac{3}{2}{{\text{n}}_{\text{1}}}{{\text{k}}_{\text{B}}}{\text{T}} + \dfrac{3}{2}{{\text{n}}_{\text{2}}}{{\text{k}}_{\text{B}}}{\text{T}}]$ 

${\text{P}} = {{\text{k}}_{\text{B}}}{\text{T}}[{{\text{n}}_1} + {{\text{n}}_2} + ....]$ 

${\text{P}} = \dfrac{{\text{R}}}{{{{\text{N}}_{\text{A}}}}}[{{\text{n}}_1} + {{\text{n}}_2} + ....]$ 

${\text{P}} = [{\mu _1} + {\mu _2} + ....]{\text{RT}}$ 

${\text{P}} = {{\text{P}}_1} + {{\text{P}}_2} + .....$ 

This is known as Dalton’s law of partial pressure.

Law of Equipartition of Energy: Degrees of Freedom

• Degrees of freedom are separate displacements or rotations that specify a body's or system's orientation.

• Three coordinates are required to define the location of a molecule that is free to move in space.

• It must move in a plane if it is limited.

• It just needs one coordinate to locate itself if it is confined to moving down a line.

• Consider a room in which a strong rope is tied from one wall to the next.

• Take a straight-moving ball and place it on the rope.

• There is only one degree of freedom for the ball. It can only move in one dimension at a time.

• Consider the situation where the ball is on a two-dimensional floor and can go in two directions.

• There are two degrees of freedom for the ball.

• Consider throwing the ball in three-dimensional space. The ball can then move in three dimensions.

• As a result, the degree of freedom indicates how many different ways a body can move, rotate, or vibrate.

Categories of Degrees of Freedom

1. Translational degree of freedom

2. Rotational degree of freedom

3. Vibrational degree of freedom

Translational Degree of Freedom

• The term "translation" refers to the movement of the entire body from one position to another.

• Consider the oxygen molecule, which is made up of two linked oxygen atoms.

• The two oxygen atoms, as well as the link, are referred to as the complete body.

• Translational movement occurs when the entire body moves from one position to another.

• Consider a molecule that is free to move in space and hence requires three coordinates to define its location (x, y, and z).

• As a result, it has three degrees of freedom.

• Similarly, a molecule that is free to move on a two-dimensional plane requires two coordinates to pinpoint its location.

• As a result, it has two degrees of freedom.

• A molecule that is free to move in a straight line requires just one coordinate to define its location.

• As a result, it only has one degree of freedom.

• Only translational degrees of freedom exist in mono-atomic gas molecules. This refers to gases with only one atom.

• For example, a single He atom makes up a Helium atom. It will have translational degrees of freedom.

• Each degree of freedom in translation adds a word containing the square of a motion variable.

• The velocity is the motion variable (vx, vy, vz).

• Energy will be contributed by the term $(\dfrac{1}{2}){\text{m}}{{\text{v}}_{\text{x}}}^2$ 

• Kinetic energy is the energy involved in the movement of a molecule from one location to another.

• The average of each of these terms in thermal equilibrium is $(\dfrac{1}{2}){{\text{k}}_{\text{B}}}{\text{T}}$ .

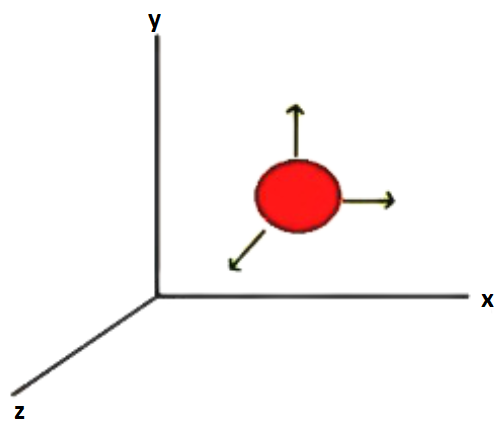
Translational Degree of Freedom

Rotational Degree of Freedom

• Independent rotations that specify a body's or system's orientation.

• A part of the body rotates about another part of the body.

• Only diatomic gases have rotational degrees of freedom.

• In addition to translational degrees of freedom, diatomic molecules have rotational degrees of freedom.

• It's feasible in diatomic compounds because two atoms are linked by a bond. As a result, the rotation of one atom in relation to another atom.

• There is a translational degree of freedom in diatomics, as well as a rotational degree of freedom.

• For instance, two oxygen atoms are connected by a bond. Two axes are perpendicular to each other.

• Along the two axes, two rotations are conceivable.

• They have three degrees of freedom in translation and two degrees of freedom in rotation.

• As a result, a component in the energy that contains the square of a rotating variable of motion is contributed by the rotational degree of freedom.

• Angular momentum is the source of the rotational variable of motion.

• Vx, vy, vz is the linear velocity. Angular velocity is written as wx, wy, wz.

• The three rotational degree of freedom along the two perpendicular axis are: ${{\text{E}}_{\text{R}}} = (\dfrac{1}{2})({{\text{I}}_1}{\omega _1}) + (\dfrac{1}{2})({{\text{I}}_2}{\omega _2})$ 

• The three translational degree of freedom will be: $\dfrac{1}{2}{m_x}{v_x}^2$ , $\dfrac{1}{2}{m_y}{v_y}^2$ and $\dfrac{1}{2}{m_z}{v_z}^2$ .

• The two rotational degrees of freedom are: $(\dfrac{1}{2})({{\text{I}}_1}^2{\omega _1}^2)$ and $(\dfrac{1}{2})({{\text{I}}_2}^2{\omega _2}^2)$ 

Vibrational Degree of Freedom

• Some molecules exhibit a mode of vibration, in which the atoms oscillate along the inter-atomic axis, similar to a one-dimensional oscillator.

• In some molecules, this vibration can be seen.

• Consider the following scenario: CO atoms oscillate like a one-dimensional oscillator along the inter-atomic axis.

• Consider two atoms that vibrate in the same direction along the inter-atomic axis.

• The vibrational energy terms include the square of vibrational motion variables.

• The total vibrational energy: ${{\text{E}}_{\text{v}}} = \dfrac{1}{2}{\text{m}}{(\dfrac{{{\text{dy}}}}{{{\text{dt}}}})^2} + \dfrac{1}{2}{\text{k}}{{\text{y}}^{\text{2}}}$ , where, $\dfrac{1}{2}{\text{m}}{(\dfrac{{{\text{dy}}}}{{{\text{dt}}}})^2}$is the kinetic energy, $\dfrac{1}{2}{\text{k}}{{\text{y}}^{\text{2}}}$ is the potential energy.

• Two terms are contributed by the vibrational degree of freedom.

The First Term is:

Two Axes Perpendicular to the Line Connecting Two Particles Rotate

The above diagram shows the two axes perpendicular to the line connecting two particles (here y and z directions)

The Second Term is:

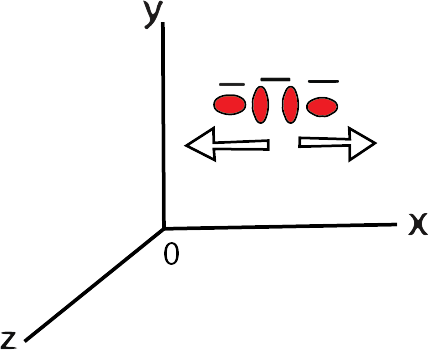
Vibrational Motion Along a Line Joining the Two Atoms

The above diagram depicts the vibrational motion along line joining the two atoms.

Comparison Between Three Energy Modes

Law of Equipartition of Energy

The total energy is equally distributed across all conceivable energy modes in equilibrium, according to this law, with each mode having an average energy equal to $\dfrac{1}{2}{{\text{k}}_{\text{B}}}{\text{T}}$ .

• $\dfrac{1}{2}{{\text{k}}_{\text{B}}}$ is contributed by each translational degree of freedom.

• Each degree of rotational freedom provides $\dfrac{1}{2}{{\text{k}}_{\text{B}}}$ .

• Each degree of vibrational freedom provides two times of $\dfrac{1}{2}{{\text{k}}_{\text{B}}}$.

Specific Heat Capacity for Monoatomic Gases

• Mono-atomic gases will only have one degree of freedom which is the translation.

• They can only have three translational degrees of freedom at most.

• Each degree of freedom will add $\dfrac{1}{2}{{\text{k}}_{\text{B}}}$  to the total.

• As a result, three degrees of freedom will each contribute $\dfrac{3}{2}{{\text{k}}_{\text{B}}}$ .

• The total internal energy of 1 mole of gas U is calculated using the law of energy equipartition. ${\text{U}} = \dfrac{3}{2}{{\text{k}}_{\text{B}}}{\text{T}}{{\text{N}}_{\text{A}}} = \dfrac{3}{2}{\text{RT}}$ 

• At constant volume, the specific heat capacity will be: ${{\text{C}}_{\text{V}}} = \dfrac{{{\text{dU}}}}{{{\text{dT}}}} = \dfrac{3}{2}{\text{R}}$ 

• For an ideal gas CP – CV = R. Now, ${{\text{C}}_{\text{P}}} = \dfrac{5}{2}{\text{R}}$ 

• The ratios of specific heat will now be: $\gamma  = \dfrac{{{{\text{C}}_{\text{P}}}}}{{{{\text{C}}_{\text{V}}}}} = \dfrac{5}{3}$ 

Specific Heat of Diatomic Gases (Non-rigid)

• A stiff diatomic gas has translational and rotational degrees of freedom but no vibrational degrees of freedom.

• They are oscillators that are stiff.

• There are three translational degrees of freedom and two rotational degrees of freedom in a stiff diatomic molecule. There are a total of 5 degrees of freedom.

• Each degree of freedom will contribute $\dfrac{1}{2}{{\text{k}}_{\text{B}}}$  according to the law of energy equi-partition.

• As a result, the fifth degree of freedom will add $\dfrac{5}{2}{{\text{k}}_{\text{B}}}$  to the total.

• The total internal energy for one mole of gas will be: ${\text{U}} = \dfrac{5}{2}{{\text{k}}_{\text{B}}}{\text{T}}{{\text{N}}_{\text{A}}} = \dfrac{5}{2}{\text{RT}}$

• At constant volume the specific heat capacity will be: ${{\text{C}}_{\text{V}}} = \dfrac{{{\text{dU}}}}{{{\text{dT}}}} = \dfrac{5}{2}{\text{R}}$

• For a rigid diatomic, the specific heat capacity at constant pressure will be given as: ${{\text{C}}_{\text{P}}} = \dfrac{7}{2}{\text{R}}$ 

• The ratios of specific heat will be: $\gamma  = \dfrac{{{{\text{C}}_{\text{P}}}}}{{{{\text{C}}_{\text{V}}}}} = \dfrac{7}{5}$

Specific Heat of Diatomic Gases (non – rigid) 

• Translational, rotational, and vibrational degrees of freedom exist in a no-rigid diatomic gas.

• There will be three degrees of freedom in translation, two degrees of freedom in rotation, and one degree of freedom in vibration.

• The total contribution by translational is $\dfrac{1}{2}{{\text{k}}_{\text{B}}}{\text{T}}$ , by rotational is two times of translational and by vibrational is ${{\text{k}}_{\text{B}}}$ 

• Total internal energy for one mole is equal to: $\dfrac{5}{2}{{\text{k}}_{\text{B}}}{\text{T}} + {{\text{k}}_{\text{B}}}{\text{T}} = \dfrac{7}{2}{{\text{k}}_{\text{B}}}{\text{T}} = \dfrac{7}{2}{\text{RT}}$ 

• ${{\text{C}}_{\text{v}}} = \dfrac{{{\text{dU}}}}{{{\text{dT}}}} = \dfrac{7}{2}{\text{R}}$ 

• ${{\text{C}}_{\text{P}}} = {{\text{C}}_{\text{V}}} + {\text{R}} = \dfrac{9}{2}{\text{R}}$ 

• $\gamma  = \dfrac{{{{\text{C}}_{\text{P}}}}}{{{{\text{C}}_{\text{V}}}}} = \dfrac{9}{7}$ 

Specific Heat for Polyatomic Molecules

• Polyatomic gases will have three degrees of freedom in translation, three degrees of freedom in rotation, and a ‘f' number of vibrational modes.

• For one mole of gas the total internal energy will be: $(\dfrac{3}{2}{{\text{k}}_{\text{B}}}{\text{T}} + \dfrac{3}{2}{{\text{k}}_{\text{B}}}{\text{T}} + {\text{f}}{{\text{k}}_{\text{B}}}{\text{T}}) \times {{\text{N}}_{\text{A}}} = (3 + {\text{f}}){\text{RT}}$ 

• ${{\text{C}}_{\text{v}}} = \dfrac{{{\text{dU}}}}{{{\text{dT}}}} = (3 + {\text{f)R}}$

• ${{\text{C}}_{\text{P}}} = {{\text{C}}_{\text{V}}} + {\text{R}} = (4 + {\text{f}}){\text{R}}$

• $\gamma  = \dfrac{{{{\text{C}}_{\text{P}}}}}{{{{\text{C}}_{\text{V}}}}} = \dfrac{{(4 + {\text{f}})}}{{(3 + {\text{f}})}}$

Specific Heat Capacity for Solids

• Consider the number of atoms in a solid, which is N. Each atom can fluctuate around its mean position.

• The degree of freedom for vibrational motion will  be: ${{\text{k}}_{\text{B}}}{\text{T}}$ 

• The average energy for one – dimensional is ${{\text{k}}_{\text{B}}}{\text{T}}$and for three – dimensional will be ${\text{3}}{{\text{k}}_{\text{B}}}{\text{T}}$.

• The total internal energy for one mole of solid will be: $3{{\text{k}}_{\text{B}}}{\text{T}}{{\text{N}}_{\text{A}}} = 3{\text{RT}}$ 

• The Volume change is very less in solids at constant pressure, \[\Delta {\text{Q}} = \Delta {\text{U}} + {\text{P}}\Delta {\text{V}}\] . So, $\Delta {\text{V}} = 0$ therefore, $\Delta {\text{Q}} = \Delta {\text{U}}$ 

• ${{\text{C}}_{\text{v}}} = {(\dfrac{{{\text{dU}}}}{{{\text{dT}}}})_{\text{V}}}$

• ${{\text{C}}_{\text{P}}} = {(\dfrac{{{\text{dQ}}}}{{{\text{dT}}}})_{\text{V}}}$ as, $\Delta {\text{Q}} = \Delta {\text{U}}$, therefore, ${{\text{C}}_{\text{v}}} = \dfrac{{{\text{dU}}}}{{{\text{dT}}}} = 3{\text{R}}$

• Therefore, ${{\text{C}}_{\text{P}}} = {{\text{C}}_{\text{V}}} = 3{\text{R}}$ 

Specific Heat Capacity of Water

• If water is considered solid, then there will be an ‘N’ number of atoms.

• So, the average energy of each atom is: $3{{\text{k}}_{\text{B}}}{\text{T}}$ 

• Therefore, there are three molecules in a water molecule ${\text{(}}{{\text{H}}_{\text{2}}}{\text{O)}}$.

• So, the total internal energy will be: ${\text{U}} = 3{{\text{k}}_{\text{B}}}{\text{T}} \times 3 \times {{\text{N}}_{\text{A}}} = 9{\text{RT}}$ 

• ${{\text{C}}_{\text{P}}} = {{\text{C}}_{\text{V}}} = 9{\text{R}}$ 

Conclusion on Specific Heat

• The specific heat determined based on the degree of freedom should be temperature-independent, according to classical mechanics.

• When the temperature is zero, however, the degree of freedom is ineffective.

• This demonstrates that classical mechanics is insufficient, necessitating the use of quantum mechanics.

• In quantum physics, a minimum amount of non-zero energy is required for degree of freedom to be active.

• As the temperature approaches zero, all substances' specific heats approach zero.

Mean Free Path

• The average distance between two successive collisions is known as the mean free path.

• Within the gas, many molecules are randomly moving and interacting with one another.

• The mean free path is the distance that a gas molecule can travel without interacting.

Expression of Mean Free Path

• Consider each gas molecule to be a sphere with a diameter of one metre (d). Each molecule's average speed is considered as ‘v’.

• Assume the molecule collides with any other molecule within a certain distance (d). Any molecule that comes within the diameter range of this molecule will collide with it.

• The volume in which the molecule suffers collision is: ${\text{v}}\Delta {\text{t}}\Pi {{\text{d}}^2}$ 

• Let the number of molecules per unit volume be ‘n’.

• Therefore, the total number of collisions will be: ${\text{v}}\Delta {\text{t}}\Pi {{\text{d}}^2}{\text{n}}$ 

• The rate of collision will be: $\dfrac{{{\text{v}}\Delta {\text{t}}\Pi {{\text{d}}^2}{\text{n}}}}{{\Delta {\text{t}}}} = {\text{v}}\Pi {{\text{d}}^2}{\text{n}}$ 

• The supposed time between collisions will be: $\tau  = \dfrac{1}{{{\text{v}}\Pi {{\text{d}}^2}{\text{n}}}}$ 

• The average distance between collisions will be: $\tau {\text{v}} = \dfrac{1}{{\Pi {{\text{d}}^2}}}$ 

• The above value $\dfrac{1}{{\Pi {{\text{d}}^2}}}$ is modified by adding a factor in it.

• Mean free path will be equal to: ${\text{l}} = \dfrac{1}{{\sqrt 2 \Pi {{\text{d}}^2}{\text{n}}}}$ 

Conclusion: The mean free path is inversely proportional to the number density that is the number of molecules per unit volume and size of the molecule.

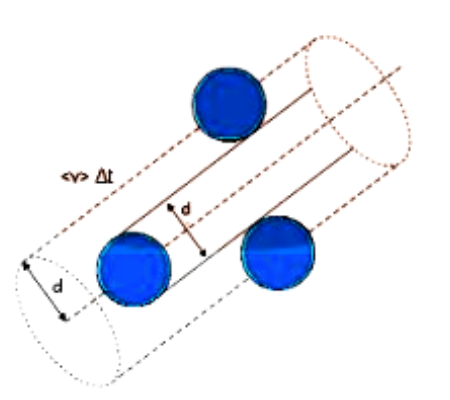
Mean Free Path

Important Topics of Class 11 Physics Chapter 12 Kinetic Theory

Important formula in Class 11 Physics Chapter 12 Kinetic Theory

1. The pressure of an Ideal Gas:
$P = \frac{1}{3} \frac{m}{V} \overline{v^2}$
Where P is pressure, mmm is mass, V is volume, and $\overline{v^2}$ is the mean square speed of gas molecules.

2. Root Mean Square Speed (RMS):
$v_{\text{rms}} = \sqrt{\frac{3kT}{m}} = \sqrt{\frac{3RT}{M}}$​​
Where $v_{\text{rms}}$ is the root mean square speed, k is the Boltzmann constant, T is the temperature, R is the universal gas constant, and M is the molar mass.

3. Ideal Gas Equation:
PV=nRT
Where P is pressure, V is volume, n is the number of moles, R is the gas constant, and T is temperature.

4. Average Kinetic Energy of a Molecule:
$E_k = \frac{3}{2} kT$
Where $E_k$​ is the average kinetic energy of a gas molecule, k is the Boltzmann constant, and T is the temperature in Kelvin.

5. Mean Free Path:
$\lambda = \frac{1}{\sqrt{2} \pi d^2 \frac{N}{V}}$​
Where $\lambda$ is the mean free path, d is the diameter of the molecule, N is the number of molecules, and V is the volume.

Importance of Class 11 Physics Chapter 12  Kinetic Theory Revision Notes 

• Class 11 Physics Kinetic Theory Notes highlight key differences between ideal and real gases, providing clarity on how theoretical concepts apply in practical situations.

• They offer step-by-step problem-solving techniques, helping students build confidence when tackling numerical questions related to gas laws and molecular motion.

• With well-organised content, the notes make it easier to revise important definitions, formulas, and theorems, which are critical for board and competitive exams.

• Class 11 Physics Kinetic Theory Notes emphasise commonly asked questions and areas of focus, allowing students to prioritise topics that are likely to appear in exams.

• They straightforwardly present complex concepts, making it easier for students to recall and apply the knowledge during exams and practical applications.

Tips for Learning the Class 11 Chapter 12 Physics Kinetic Theory:

• Start by understanding the basic concepts like molecular motion and how gas particles behave, as these are fundamental to the chapter.

• Focus on the key laws (Boyle’s law, Charles’s law, and Avogadro’s law) and understand how they are connected to the behaviour of gases.

• Practice solving problems related to gas laws to strengthen your understanding of the formulas and their applications.

• Visualise how temperature affects the speed and energy of gas particles, which helps in grasping the relationship between temperature and kinetic energy.

• Break down complex formulas step by step, and remember their practical applications to connect theory with real-world examples.

• Regularly revise important terms like mean free path, pressure, and volume, as these are essential for solving numerical questions.

• Relating the concepts to everyday examples, such as how balloons expand or contract, can make learning easier.

Conclusion 

The Kinetic Theory in Class 11 Physics helps students understand how gases behave by exploring molecular motion and energy. This chapter simplifies the behaviour of gas particles and explains key laws like Boyle’s and Charles’s laws, showing how pressure, volume, and temperature are related. Through these concepts, students can see the connection between theory and real-life applications. The revision notes for this chapter make complex ideas easier to grasp, helping with exam preparation and improving problem-solving skills. Understanding this topic is important for building a strong foundation in physics, especially for further studies in thermodynamics and related areas.

Related Study Materials for Class 12 Physics Chapter 12

Chapter-wise Links for Physics Notes For Class 11 PDF FREE Download

Related Study Materials Links for Class 11 Physics

Along with this, students can also download additional study materials provided by Vedantu for Physics Class 11–