Maths Notes for Chapter 7 Coordinate Geometry Class 10 - FREE PDF Download
Coordinate Geometry Class 10 Maths Chapter 7 CBSE Notes - 2025-26



FAQs on Coordinate Geometry Class 10 Maths Chapter 7 CBSE Notes - 2025-26
1. What is coordinate geometry in Class 10 Maths, and why is it important for revision notes?
Coordinate geometry in Class 10 Maths is the study of geometric figures using a coordinate plane and algebraic principles. It enables students to understand concepts like distance, area, centroid, and dividing line segments through formulas. Mastery of coordinate geometry Class 10 notes is vital for quick revision, clear concept retention, and accurate problem-solving in board exams.
2. Which are the key formulas covered under Coordinate Geometry Class 10 revision notes as per CBSE 2025-26?
Key formulas in Class 10 Coordinate Geometry include:
- Distance Formula: AB = √[(x₂ - x₁)² + (y₂ - y₁)²]
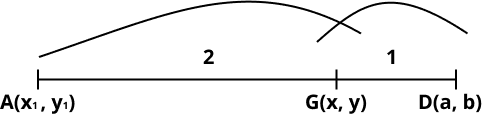
- Section Formula (internal division): (mx₂ + nx₁)/(m + n), (my₂ + ny₁)/(m + n)
- Midpoint Formula: ((x₁ + x₂)/2, (y₁ + y₂)/2)
- Area of Triangle: ½[x₁(y₂–y₃) + x₂(y₃–y₁) + x₃(y₁–y₂)]
- Centroid: ((x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3)
3. How should students ideally use Coordinate Geometry Class 10 notes for effective revision?
To get the best results from Coordinate Geometry Class 10 revision notes:
- Summarize each formula separately.
- Make a list of key terms and their meanings.
- Practice example problems immediately after revising the concept.
- Relate concepts between distance, section, and area formulas for better retention.
- Revise regularly for better recall during exams.
4. What are the most important topics highlighted in Class 10 Coordinate Geometry revision notes?
The most important topics for Class 10 Coordinate Geometry notes include:
- Distance formula
- Section formula and Midpoint formula
- Area of triangle using vertices
- Centroid of a triangle
- Concept of collinearity and its test
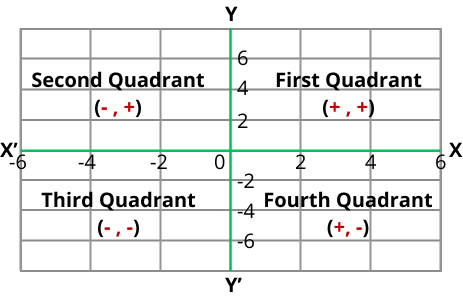
- Understanding the Cartesian plane and quadrants
5. What conceptual mistakes do students commonly make while preparing Coordinate Geometry Class 10 for exams?
Common mistakes with coordinate geometry Class 10 concepts are:
- Swapping coordinates or sign errors in formulas
- Forgetting to take the absolute value in the area of triangle calculations
- Incorrectly applying section formula for external division
- Mistaking midpoint for centroid
- Not verifying if points are collinear when required
6. How are the Distance Formula and Section Formula connected in Coordinate Geometry revision for Class 10?
Both the distance formula and section formula in coordinate geometry use the coordinates of points on the Cartesian plane to find geometric properties. The distance formula measures the length between two points, while the section formula finds the coordinates of a point dividing a segment in a specific ratio. Understanding their relationship aids in solving advanced geometry questions efficiently.
7. Why is it necessary to use the absolute value when calculating the area of a triangle in Coordinate Geometry Class 10?
The area of a triangle formula can yield a negative value if the vertices are not ordered anticlockwise. Using the absolute value ensures the area is always a positive quantity, as area cannot be negative according to mathematical convention and CBSE norms.
8. How do you determine if three points are collinear using the Coordinate Geometry formulas in Class 10 revision notes?
If the area of a triangle formed by three given points is zero using the coordinate formula, then those points are said to be collinear. This test is frequently cited in Class 10 CBSE board exam questions.
9. In Coordinate Geometry Class 10, how is the centroid of a triangle calculated and what is its significance?
The centroid of a triangle with vertices (x₁, y₁), (x₂, y₂), (x₃, y₃) is calculated as ((x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3). It represents the point of intersection of the medians and is also the triangle's center of mass, useful for dividing triangles into equal-area sub-triangles.
10. What is the revision order recommended for Class 10 Coordinate Geometry topics as per CBSE guidelines?
The best revision order for Coordinate Geometry Class 10 is:
- Basics of Cartesian plane, axes, and coordinates
- Distance formula
- Section and midpoint formulas
- Area of triangle and test for collinearity
- Centroid and area of polygons (if included)
11. What real-life applications can be understood from the Coordinate Geometry Class 10 revision notes?
Coordinate geometry concepts such as distance and section formulas are used in navigation, map reading, architecture, computer graphics, and physics problems involving movement in planes. Recognizing these applications helps students relate theory to practical scenarios, a skill valued by CBSE examiners.
12. How does the Midpoint Formula differ from the Section Formula in the context of Class 10 Coordinate Geometry?
The midpoint formula is a special case of the section formula where the line is divided in a 1:1 ratio. The midpoint gives the coordinates exactly halfway between two end points, while the section formula finds a division point in any arbitrary ratio m:n. Understanding this connection streamlines revision and clarifies related exam questions.
13. What key terms should be memorized from the Coordinate Geometry Class 10 revision notes for definition-based questions?
Essential coordinate geometry vocabulary includes:
- Abscissa
- Ordinate
- Origin
- Centroid
- Collinear points
- Section and Midpoint
- Quadrants of a Cartesian plane
14. How can students quickly spot errors in their answers while revising with Class 10 Coordinate Geometry notes?
To quickly spot errors in coordinate geometry revision:
- Check if signs for differences (x₂-x₁, y₂-y₁) are used correctly.
- Verify if absolute value is applied in the area formula.
- Confirm correct ratios in section/midpoint formulas.
- Cross-check if the answer is logically possible (e.g., area cannot be negative; midpoint should lie between given points).




















 Watch Video
Watch Video