
Write two differences between speed and velocity?
Answer
535.2k+ views
Hint: The rate of change of position over time is a very important quantity. We can say that it is velocity or speed and at a first glance it seems to be the same but both velocity and speed are a difference by its properties but they are not the same.
Complete step-by-step answer:
As mentioned above both speed and velocity are different from each other, but both of them are the rate of change of position so the question arrives why they are different?
Let’s find it.
Speed: The distance traveled by the particle in space (it may be in 1-dimensional, 2-dimensional or 3-dimensional) in some time interval is called speed.
Velocity: The displacement by the particle in space in some time interval is called velocity.
Now it seems difficult to find out the difference between both of them.
Let’s take an example,
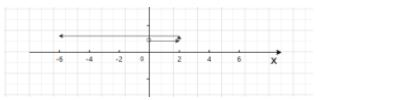
In the figure my car starts to travel from \[0\], then it goes \[2m\] in right and from there it goes \[8m\] in left in time \[60\sec \]. The distance travelled by car is \[2m+8m\]. But displacement is \[6m\] towards the left only. So when we find speed, it is \[\dfrac{2+8}{60}=0.17m\text{ }{{\text{s}}^{-1}}\] but velocity is \[\dfrac{-6}{60}=-0.1\text{ }m\text{ }{{\text{s}}^{-1}}\].
Now let’s see some important difference between speed and velocity.
Additional Information: Scalar quantity: Some quantity can only be described by only numerical values with specified units and we can add by normal rules of algebra is called a scalar quantity.
Vector quantity: Some quantity can be described by numerical values as well as the direction in space with specified units and we cannot add by normal rules of algebra is called a vector quantity.
Note:
1) The dimensions of both the quantities are (\[L{{T}^{-1}}\] ) the same but both quantities are not the same.
2) Speed depends on the path of the particle covered but velocity is the path difference of the particle covered (we simply say that velocity is dependent on start point and endpoint).
Complete step-by-step answer:
As mentioned above both speed and velocity are different from each other, but both of them are the rate of change of position so the question arrives why they are different?
Let’s find it.
Speed: The distance traveled by the particle in space (it may be in 1-dimensional, 2-dimensional or 3-dimensional) in some time interval is called speed.
Velocity: The displacement by the particle in space in some time interval is called velocity.
Now it seems difficult to find out the difference between both of them.
Let’s take an example,

In the figure my car starts to travel from \[0\], then it goes \[2m\] in right and from there it goes \[8m\] in left in time \[60\sec \]. The distance travelled by car is \[2m+8m\]. But displacement is \[6m\] towards the left only. So when we find speed, it is \[\dfrac{2+8}{60}=0.17m\text{ }{{\text{s}}^{-1}}\] but velocity is \[\dfrac{-6}{60}=-0.1\text{ }m\text{ }{{\text{s}}^{-1}}\].
Now let’s see some important difference between speed and velocity.
| Speed | Velocity |
| 1. It is the time rate of change in distance. | 1. It is the time rate of change in displacement. |
| 2. It is a scalar quantity. | 2. It is a vector quantity. (Note that in above example we take displacement \[=-6m\]) |
| 3. \[v=\dfrac{\Delta x}{\Delta t}\] | 3. \[\overset{\to }{\mathop{v}}\,=\dfrac{\overset{\to }{\mathop{ds}}\,}{dt}\] |
Additional Information: Scalar quantity: Some quantity can only be described by only numerical values with specified units and we can add by normal rules of algebra is called a scalar quantity.
Vector quantity: Some quantity can be described by numerical values as well as the direction in space with specified units and we cannot add by normal rules of algebra is called a vector quantity.
Note:
1) The dimensions of both the quantities are (\[L{{T}^{-1}}\] ) the same but both quantities are not the same.
2) Speed depends on the path of the particle covered but velocity is the path difference of the particle covered (we simply say that velocity is dependent on start point and endpoint).
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Trending doubts
1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Proton was discovered by A Thomson B Rutherford C Chadwick class 11 chemistry CBSE

Draw a diagram of nephron and explain its structur class 11 biology CBSE

How do you find the composite numbers from 1 to 50 class 11 maths CBSE




