
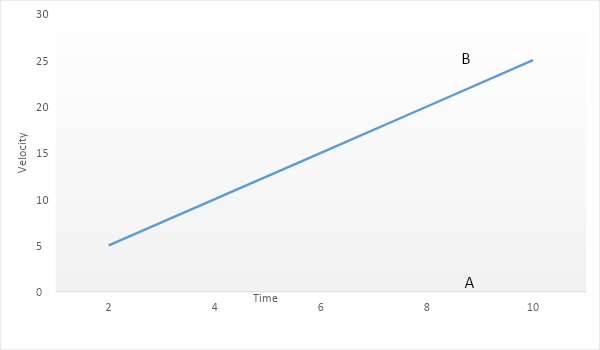
The speed of a car as a function of time is shown in the figure. Find the distance travelled by the car in 8 seconds and its acceleration.

Answer
521.4k+ views
Hint
To find out the distance travelled by the car and its acceleration, we need to know about the relations between the velocity, acceleration and distance of the car. Velocity is equal to the displacement of the car in a particular given time. In this question, speed and velocity of the car is the same as the distance and displacement is the same.
$\Rightarrow a = \dfrac{{dv}}{{dt}}$
And, $S = ut + \dfrac{1}{2}a{t^2}$
Where, S is the distance travelled by the car, u is the initial velocity, t is the time taken for covering the distance S, and a is the acceleration of the car.
Complete step by step answer
As we know, the velocity/speed of the car is given by,
$\Rightarrow v = \dfrac{d}{t}$
Now, the acceleration is given by the velocity of the car per unit time. This can be written as,
$\Rightarrow a = \dfrac{v}{t}$
In differential form,
$\Rightarrow a = \dfrac{{dv}}{{dt}}$
Which is also equal to the slope of the graph.
Thus,
$\Rightarrow a = \dfrac{{dv}}{{dt}} = slope = \dfrac{{AB}}{{OA}}$
$\Rightarrow \dfrac{{AB}}{{OA}} = \dfrac{{20}}{8}$
So, the acceleration of the car is,
$\Rightarrow a = \dfrac{5}{2} = 2.5m/{s^2}$
Now, we have to find out the distance using one of the equations of motion. It comes as,
$\Rightarrow S = ut + \dfrac{1}{2}a{t^2}$
Where, S is the distance travelled by the car, u is the initial velocity, t is the time taken for covering the distance S, and a is the acceleration of the car.
By substituting the values in the above equation,
$\Rightarrow S = 0 \times t + \dfrac{1}{2} \times 2.5 \times {\left( 8 \right)^2}$ ….. (∵ u is the initial velocity of the car and is 0, t=8, a=2.5)
$\Rightarrow S = 80m$
Hence, the distance travelled by the car in 8 seconds is 80m and its acceleration is $2.5m/s^2$.
Note
We can also find out the distance travelled by the car using an alternative method. We know that the area under the v-t graph gives distance, as the displacement as a function of t gives velocity.
Then, the area under the triangle OAB =$\dfrac{1}{2} \times base \times height$ $\Rightarrow \dfrac{1}{2} \times 8 \times 20$
Thus, we get the distance travelled as 80m from this method also.
To find out the distance travelled by the car and its acceleration, we need to know about the relations between the velocity, acceleration and distance of the car. Velocity is equal to the displacement of the car in a particular given time. In this question, speed and velocity of the car is the same as the distance and displacement is the same.
$\Rightarrow a = \dfrac{{dv}}{{dt}}$
And, $S = ut + \dfrac{1}{2}a{t^2}$
Where, S is the distance travelled by the car, u is the initial velocity, t is the time taken for covering the distance S, and a is the acceleration of the car.
Complete step by step answer
As we know, the velocity/speed of the car is given by,
$\Rightarrow v = \dfrac{d}{t}$
Now, the acceleration is given by the velocity of the car per unit time. This can be written as,
$\Rightarrow a = \dfrac{v}{t}$
In differential form,
$\Rightarrow a = \dfrac{{dv}}{{dt}}$
Which is also equal to the slope of the graph.
Thus,
$\Rightarrow a = \dfrac{{dv}}{{dt}} = slope = \dfrac{{AB}}{{OA}}$
$\Rightarrow \dfrac{{AB}}{{OA}} = \dfrac{{20}}{8}$
So, the acceleration of the car is,
$\Rightarrow a = \dfrac{5}{2} = 2.5m/{s^2}$
Now, we have to find out the distance using one of the equations of motion. It comes as,
$\Rightarrow S = ut + \dfrac{1}{2}a{t^2}$
Where, S is the distance travelled by the car, u is the initial velocity, t is the time taken for covering the distance S, and a is the acceleration of the car.
By substituting the values in the above equation,
$\Rightarrow S = 0 \times t + \dfrac{1}{2} \times 2.5 \times {\left( 8 \right)^2}$ ….. (∵ u is the initial velocity of the car and is 0, t=8, a=2.5)
$\Rightarrow S = 80m$
Hence, the distance travelled by the car in 8 seconds is 80m and its acceleration is $2.5m/s^2$.
Note
We can also find out the distance travelled by the car using an alternative method. We know that the area under the v-t graph gives distance, as the displacement as a function of t gives velocity.
Then, the area under the triangle OAB =$\dfrac{1}{2} \times base \times height$ $\Rightarrow \dfrac{1}{2} \times 8 \times 20$
Thus, we get the distance travelled as 80m from this method also.
Recently Updated Pages
Biology Explained: Branches, Topics & Essentials

Cesarean Section: Definition, Indications, Types & Recovery

Beriberi: Causes, Types, Symptoms & Prevention Explained

Fundamentals of Chemistry: Organic, Inorganic & Physical

Archaebacteria: Definition, Features & Differences Simplified

Chemical Compounds: Types, Examples & Properties Explained

Trending doubts
1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Proton was discovered by A Thomson B Rutherford C Chadwick class 11 chemistry CBSE

Draw a diagram of nephron and explain its structur class 11 biology CBSE




