
The correct expression for Lorentz force is
(A) $q\left[ {\vec E + \left( {\vec B \times \vec V} \right)} \right]$
(B) $q\left[ {\vec E + \left( {\vec V \times \vec B} \right)} \right]$
(C) $q\left( {\vec V \times \vec B} \right)$
(D) $q\vec E$
Answer
219.3k+ views
Hint Before solving this problem, we have to remember that a charged particle moving through a magnetic field experiences a force, which is at the right angle to both the direction in which the particle is moving and the direction of the applied magnetic field. This force is called the Lorentz force.
Complete Step-by-step solution
Lorentz force is defined as the mixture of the magnetic force and the electric force on a point charge when placed in an electromagnetic field. The Lorentz force is used in electromagnetism, a combination of electricity and magnetism, and is also known as the electromagnetic force.
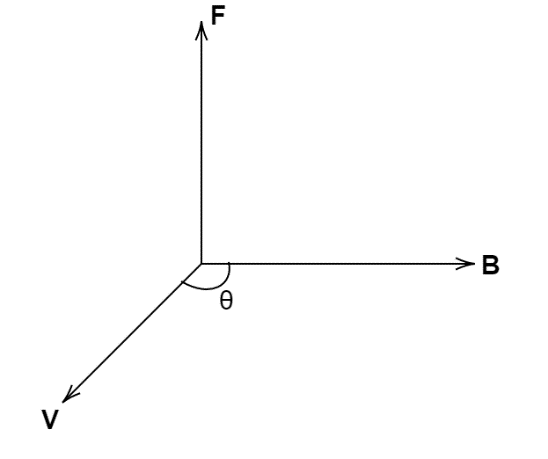
The electric force on a charged particle is,
${\vec F_E} = q\vec E$
where,
$q$ is the electric charge on the particle.
$\vec E$ is the external electric field.
Magnetic force on a charged particle is,
${\vec F_B} = q\left( {\vec V \times \vec B} \right)$
${\vec F_B} = qVB\sin \theta $
$q$ is the electric charge on the particle.
$V$ is the velocity of the particle.
$B$ is the external magnetic field.
$\theta $ is the angle between velocity and the magnetic field.
The expression for the Lorentz force experienced by a charged particle is given as:
$\vec F = {\vec F_E} + {\vec F_B}$
On putting the value of ${\vec F_E}$ and${\vec F_B}$, we get
$\vec F = q\vec E + q\left( {\vec V \times \vec B} \right)$
Taking the $q$ common out, we get
$\vec F = q\left[ {\vec E + \left( {\vec V \times \vec B} \right)} \right]$
Lorentz force helps to clarify the mathematical equations along with the physical significance of the forces, electric force and magnetic force, acting on the charged particles that are traveling through the space having the electric field as well as the magnetic field. This is the importance of the Lorentz force.
So, the correct answer is (B) $q\left[ {\vec E + \left( {\vec V \times \vec B} \right)} \right]$ .
Additional Information
The applications of the Lorentz force are:
1. Cyclotrons and other particle accelerators use the phenomenon of Lorentz force.
2. A bubble chamber uses Lorentz force to generate the graph for getting the trajectories of the charged particles
3. Cathode ray tube televisions use the concept of Lorentz force to deviate the path of the electrons in a straight line to make them land on the specific spots on the screen.
Note The Lorentz force is the force exerted on an electrically charged particle that moves through a magnetic field and electric field. The Lorentz force is composed of two vector components, one proportional to the magnetic field and the other proportional to the electric field. These components must be added in vector form, to obtain the total force.
Complete Step-by-step solution
Lorentz force is defined as the mixture of the magnetic force and the electric force on a point charge when placed in an electromagnetic field. The Lorentz force is used in electromagnetism, a combination of electricity and magnetism, and is also known as the electromagnetic force.

The electric force on a charged particle is,
${\vec F_E} = q\vec E$
where,
$q$ is the electric charge on the particle.
$\vec E$ is the external electric field.
Magnetic force on a charged particle is,
${\vec F_B} = q\left( {\vec V \times \vec B} \right)$
${\vec F_B} = qVB\sin \theta $
$q$ is the electric charge on the particle.
$V$ is the velocity of the particle.
$B$ is the external magnetic field.
$\theta $ is the angle between velocity and the magnetic field.
The expression for the Lorentz force experienced by a charged particle is given as:
$\vec F = {\vec F_E} + {\vec F_B}$
On putting the value of ${\vec F_E}$ and${\vec F_B}$, we get
$\vec F = q\vec E + q\left( {\vec V \times \vec B} \right)$
Taking the $q$ common out, we get
$\vec F = q\left[ {\vec E + \left( {\vec V \times \vec B} \right)} \right]$
Lorentz force helps to clarify the mathematical equations along with the physical significance of the forces, electric force and magnetic force, acting on the charged particles that are traveling through the space having the electric field as well as the magnetic field. This is the importance of the Lorentz force.
So, the correct answer is (B) $q\left[ {\vec E + \left( {\vec V \times \vec B} \right)} \right]$ .
Additional Information
The applications of the Lorentz force are:
1. Cyclotrons and other particle accelerators use the phenomenon of Lorentz force.
2. A bubble chamber uses Lorentz force to generate the graph for getting the trajectories of the charged particles
3. Cathode ray tube televisions use the concept of Lorentz force to deviate the path of the electrons in a straight line to make them land on the specific spots on the screen.
Note The Lorentz force is the force exerted on an electrically charged particle that moves through a magnetic field and electric field. The Lorentz force is composed of two vector components, one proportional to the magnetic field and the other proportional to the electric field. These components must be added in vector form, to obtain the total force.
Recently Updated Pages
Chemical Equation - Important Concepts and Tips for JEE

JEE Main 2022 (July 29th Shift 1) Chemistry Question Paper with Answer Key

Conduction Explained: Definition, Examples & Science for Students

Analytical Method of Vector Addition Explained Simply

Atomic Size - Important Concepts and Tips for JEE

JEE Main 2022 (June 29th Shift 1) Maths Question Paper with Answer Key

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Understanding Uniform Acceleration in Physics

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Understanding Atomic Structure for Beginners

How to Convert a Galvanometer into an Ammeter or Voltmeter

Understanding Centrifugal Force in Physics

JEE Main Marking Scheme 2026- Paper-Wise Marks Distribution and Negative Marking Details

Degree of Dissociation: Meaning, Formula, Calculation & Uses




