
The coefficient of linear expansion of a cubical crystal along three mutually perpendicular directions is ${\alpha _1}$ ${\alpha _2}$ and ${\alpha _3}$ . What is the coefficient of cubical expansion of the crystal?
Answer
363.6k+ views
Hint: You may start with a cuboid and set the temperature to rise from ${0^ \circ }C$ to ${T^ \circ }C$ as a first step. Then you might find the linear expansion equation in all three dimensions. The volume of the solid will then be determined by taking their product. You can get an expression by expanding that expression and then ignoring the smaller terms. You may figure out the answer by comparing it to the volume expansion expression.
Complete answer:
Considering a cubical crystal structure
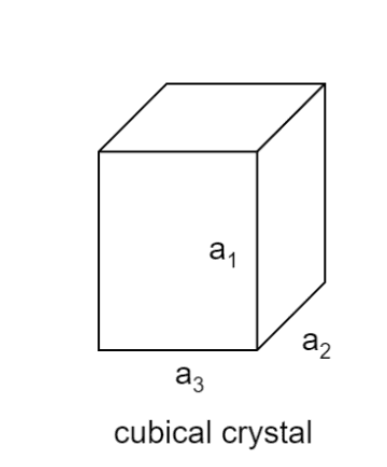
Let ${\alpha _1}$ ${\alpha _2}$ and ${\alpha _3}$ . be the coefficient of linear expression along the sides is ${a_1}$ ${a_2}$ and ${a_3}$.
We know for linear expansion
$a = {a_0}(1 + \alpha \Delta T)$
Where ${a_0}$ is the initial edge length
Take the temperature of the solid above to rise from ${0^ \circ }C$ to ${T^ \circ }C$
\[\Delta T = T - 0 = T\]
So for all the edges we have
\[{a_1}\prime = {a_1}(1 + {\alpha _1}T)\]
\[{a_2}\prime = {a_2}(1 + {\alpha _2}T)\]
\[{a_3}\prime = {a_3}(1 + {\alpha _3}T)\]
After expansion, their product will give the volume of the cuboid at temperature ${T^ \circ }C$ .
\[V\prime = {a_1}\prime {a_2}\prime {a_3}\prime = {a_1}{a_2}{a_3}(1 + {\alpha _1}T)(1 + {\alpha _2}T)(1 + {\alpha _3}T)\]
However, we know that the cuboid's initial volume is determined by the product of the edges. That is to say,
\[{V_0} = {a_1}{a_2}{a_3}\]
By neglecting small values from the above equation we get
\[V\prime \approx {V_0}(1 + ({\alpha _1} + {\alpha _2} + {\alpha _3})T)\]
Now using the formula of volume expansion
\[V = {V_0}(1 + \gamma \Delta T)\]
Comparing this from the above equation we get
\[\gamma = {\alpha _1} + {\alpha _2} + {\alpha _3}\]
Note:
Thermal expansion is the phrase used to describe the tendency of matter to change in length, area, and volume as a result of temperature changes. When molecules are heated, they move and vibrate more, increasing the space between them. The ratio of relative expansion to temperature change can be characterised as the coefficient of thermal expansion.
Complete answer:
Considering a cubical crystal structure

Let ${\alpha _1}$ ${\alpha _2}$ and ${\alpha _3}$ . be the coefficient of linear expression along the sides is ${a_1}$ ${a_2}$ and ${a_3}$.
We know for linear expansion
$a = {a_0}(1 + \alpha \Delta T)$
Where ${a_0}$ is the initial edge length
Take the temperature of the solid above to rise from ${0^ \circ }C$ to ${T^ \circ }C$
\[\Delta T = T - 0 = T\]
So for all the edges we have
\[{a_1}\prime = {a_1}(1 + {\alpha _1}T)\]
\[{a_2}\prime = {a_2}(1 + {\alpha _2}T)\]
\[{a_3}\prime = {a_3}(1 + {\alpha _3}T)\]
After expansion, their product will give the volume of the cuboid at temperature ${T^ \circ }C$ .
\[V\prime = {a_1}\prime {a_2}\prime {a_3}\prime = {a_1}{a_2}{a_3}(1 + {\alpha _1}T)(1 + {\alpha _2}T)(1 + {\alpha _3}T)\]
However, we know that the cuboid's initial volume is determined by the product of the edges. That is to say,
\[{V_0} = {a_1}{a_2}{a_3}\]
By neglecting small values from the above equation we get
\[V\prime \approx {V_0}(1 + ({\alpha _1} + {\alpha _2} + {\alpha _3})T)\]
Now using the formula of volume expansion
\[V = {V_0}(1 + \gamma \Delta T)\]
Comparing this from the above equation we get
\[\gamma = {\alpha _1} + {\alpha _2} + {\alpha _3}\]
Note:
Thermal expansion is the phrase used to describe the tendency of matter to change in length, area, and volume as a result of temperature changes. When molecules are heated, they move and vibrate more, increasing the space between them. The ratio of relative expansion to temperature change can be characterised as the coefficient of thermal expansion.
Recently Updated Pages
Glucose when reduced with HI and red Phosphorus gives class 11 chemistry CBSE

The highest possible oxidation states of Uranium and class 11 chemistry CBSE

Find the value of x if the mode of the following data class 11 maths CBSE

Which of the following can be used in the Friedel Crafts class 11 chemistry CBSE

A sphere of mass 40 kg is attracted by a second sphere class 11 physics CBSE

Statement I Reactivity of aluminium decreases when class 11 chemistry CBSE

Trending doubts
10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

State and prove Bernoullis theorem class 11 physics CBSE

What organs are located on the left side of your body class 11 biology CBSE

How many valence electrons does nitrogen have class 11 chemistry CBSE




