
State and prove Bernoulli’s theorem.
Answer
500k+ views
Hint: Here, we first know what Bernoulli's principle states, and then further we can prove the theorem by deriving the expression which relates the pressure and potential energy of the fluid. At last we will also note down the limitations of this theorem.
Formula used:
$\eqalign{
& K.{E_{gained}} = \dfrac{1}{2}\rho ({v_2}^2 - {v_1}^2) \cr
& P.{E_{gained}} = \rho g({h_2} - {h_1}) \cr} $
Complete answer:
Bernoulli's principle states that an increase in the speed of a fluid occurs simultaneously with a decrease in static pressure or a decrease in the fluid's potential energy.
To prove Bernoulli's theorem, consider a fluid of negligible viscosity moving with laminar flow, as shown in Figure.
Let the velocity, pressure and area of the fluid column be ${p_1}$, ${v_1}$ and ${A_1}$ at Q and ${p_2}$, ${v_2}$ and ${A_2}$ at R. Let the volume bounded by Q and R move to S and T where QS =${L_1}$, and RT = ${L_2}$.
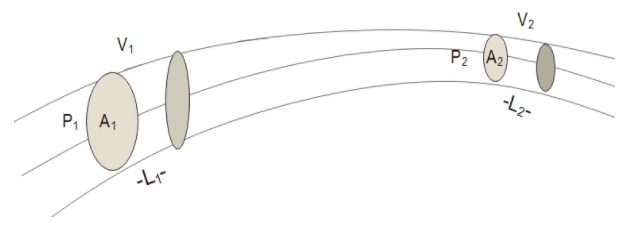
If the fluid is incompressible:
The work done by the pressure difference per unit volume = gain in kinetic energy per unit volume + gain in potential energy per unit volume. Now:
${A_1}{L_1} = {A_2}{L_2}$
Work done is given by:
$\eqalign{& W = F \times d = p \times volume \cr
& \Rightarrow {W_{net}} = {p_1} - {p_2} \cr} $
$\eqalign{& \Rightarrow K.E = \dfrac{1}{2}m{v^2} = \dfrac{1}{2}V\rho {v^2} = \dfrac{1}{2}\rho {v^2}(\because V = 1) \cr
& \Rightarrow K.{E_{gained}} = \dfrac{1}{2}\rho ({v_2}^2 - {v_1}^2) \cr} $
$\eqalign{& {P_1} + \dfrac{1}{2}\rho {v_1}^2 + \rho g{h_1} = {P_2} + \dfrac{1}{2}\rho {v_2}^2 + \rho g{h_2} \cr
& \therefore P + \dfrac{1}{2}\rho {v^2} + \rho gh = const. \cr} $
For a horizontal tube
$\eqalign{& \because {h_1} = {h_2} \cr
& \therefore P + \dfrac{1}{2}\rho {v^2} = const. \cr} $
Therefore, this proves Bernoulli's theorem. Here we can see that if there is an increase in velocity there must be a decrease in pressure and vice versa.
Additional information:
Bernoulli's principle is named after Daniel Bernoulli who published this in his book Hydrodynamica in 1738.
Pressure applied on an object is given by the force exerted on the object per unit area. The S.I unit of pressure is Pascal.
Work done on an object is defined as the force applied on the object for a certain displacement. Further, if we define a volume, it is the quantity of three-dimensional space enclosed by a closed surface.
Note:
We should remember that no fluid is totally incompressible whereas in practice the general qualitative assumptions still hold for real fluids. One should also notice that in Bernoulli's theorem, it is given that the velocity of every particle of liquid across any cross-section is uniform which is not correct, because the velocity of the particles is different in different layers.
Formula used:
$\eqalign{
& K.{E_{gained}} = \dfrac{1}{2}\rho ({v_2}^2 - {v_1}^2) \cr
& P.{E_{gained}} = \rho g({h_2} - {h_1}) \cr} $
Complete answer:
Bernoulli's principle states that an increase in the speed of a fluid occurs simultaneously with a decrease in static pressure or a decrease in the fluid's potential energy.
To prove Bernoulli's theorem, consider a fluid of negligible viscosity moving with laminar flow, as shown in Figure.
Let the velocity, pressure and area of the fluid column be ${p_1}$, ${v_1}$ and ${A_1}$ at Q and ${p_2}$, ${v_2}$ and ${A_2}$ at R. Let the volume bounded by Q and R move to S and T where QS =${L_1}$, and RT = ${L_2}$.

If the fluid is incompressible:
The work done by the pressure difference per unit volume = gain in kinetic energy per unit volume + gain in potential energy per unit volume. Now:
${A_1}{L_1} = {A_2}{L_2}$
Work done is given by:
$\eqalign{& W = F \times d = p \times volume \cr
& \Rightarrow {W_{net}} = {p_1} - {p_2} \cr} $
$\eqalign{& \Rightarrow K.E = \dfrac{1}{2}m{v^2} = \dfrac{1}{2}V\rho {v^2} = \dfrac{1}{2}\rho {v^2}(\because V = 1) \cr
& \Rightarrow K.{E_{gained}} = \dfrac{1}{2}\rho ({v_2}^2 - {v_1}^2) \cr} $
$\eqalign{& {P_1} + \dfrac{1}{2}\rho {v_1}^2 + \rho g{h_1} = {P_2} + \dfrac{1}{2}\rho {v_2}^2 + \rho g{h_2} \cr
& \therefore P + \dfrac{1}{2}\rho {v^2} + \rho gh = const. \cr} $
For a horizontal tube
$\eqalign{& \because {h_1} = {h_2} \cr
& \therefore P + \dfrac{1}{2}\rho {v^2} = const. \cr} $
Therefore, this proves Bernoulli's theorem. Here we can see that if there is an increase in velocity there must be a decrease in pressure and vice versa.
Additional information:
Bernoulli's principle is named after Daniel Bernoulli who published this in his book Hydrodynamica in 1738.
Pressure applied on an object is given by the force exerted on the object per unit area. The S.I unit of pressure is Pascal.
Work done on an object is defined as the force applied on the object for a certain displacement. Further, if we define a volume, it is the quantity of three-dimensional space enclosed by a closed surface.
Note:
We should remember that no fluid is totally incompressible whereas in practice the general qualitative assumptions still hold for real fluids. One should also notice that in Bernoulli's theorem, it is given that the velocity of every particle of liquid across any cross-section is uniform which is not correct, because the velocity of the particles is different in different layers.
Recently Updated Pages
Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Class 11 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

What is the technique used to separate the components class 11 chemistry CBSE

Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

Give two reasons to justify a Water at room temperature class 11 chemistry CBSE

Try out challenging quizzes on this topic
made by experts!
made by experts!
Take me there!



