
A sphere of mass 40 kg is attracted by a second sphere of mass 15kg, when their centers are 20cm apart, with a force of 0.1 milligram weight. Calculate the value of gravitational constant.
$
A.\,8.53 \times {10^{ - 11}}N{m^2}k{g^{ - 2}} \\
B.\,6.53 \times {10^{ - 11}}N{m^2}k{g^{ - 2}} \\
C.\,7.53 \times {10^{ - 11}}N{m^2}k{g^{ - 2}} \\
D.\,9 \times {10^{ - 11}}N{m^2}k{g^{ - 2}} \\
$
Answer
449.1k+ views
Hint: In order to solve this problem we need to use the formula of force and then we have to put all the values and get the value of the gravitational constant. The main thing here is to get the force in Newton since it is given in milligram weight so first we will convert the force and then put the values to get the right answer.
Complete answer:
It is said that a sphere of mass 40 kg is attracted by a second sphere of mass 15kg, when their centers are 20cm apart, with a force of 0.1 milligram weight. We need to calculate the value of G here.
The situation of this problem can be denoted in figure as:
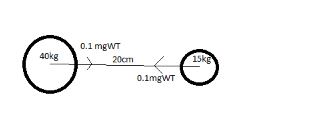
The spheres are 20cm(0.2m) apart and the force between them is 0.1miligram weight.
We know that 1 mg weight = ${10^{ - 3}} \times 980dyne$.
Therefore 0.1 mg weight = 98 x ${10^{ - 3}}$dyne
We also know that 1 dyne = ${10^{ - 5}}N$
So, 98 $\times$ ${10^{ - 3}}$dyne = $98 \times {10^{ - 8}}$ = F.
The formula of gravitational force between two masses m1 and m2 and the distance between them as r is,
F = $\dfrac{{G{m_1}{m_2}}}{{{r^2}}}$.
On putting the respective values we get the values of G as:
$ \Rightarrow G = \dfrac{{F{{(r)}^2}}}{{{m_1}{m_2}}} = \dfrac{{98 \times {{10}^{ - 8}} \times 0.2 \times 0.2}}{{40 \times 15}} = 6.53 \times {10^{ - 11}}$ .
Therefore the value of gravitational constant G here is $6.53 \times {10^{ - 11}}N{m^2}k{g^{ - 2}}$.
So, the correct answer is “Option B”.
Note:
Here one needs to know the conversion of units that is 1 dyne = ${10^{ - 5}}N$ and 1g weight = 980 dyne. Then we have done the conversion and used the formula of gravitational force between two bodies that is F = $\dfrac{{G{m_1}{m_2}}}{{{r^2}}}$. Knowing these things and proceeding like this will take you to the right answer.
Complete answer:
It is said that a sphere of mass 40 kg is attracted by a second sphere of mass 15kg, when their centers are 20cm apart, with a force of 0.1 milligram weight. We need to calculate the value of G here.
The situation of this problem can be denoted in figure as:

The spheres are 20cm(0.2m) apart and the force between them is 0.1miligram weight.
We know that 1 mg weight = ${10^{ - 3}} \times 980dyne$.
Therefore 0.1 mg weight = 98 x ${10^{ - 3}}$dyne
We also know that 1 dyne = ${10^{ - 5}}N$
So, 98 $\times$ ${10^{ - 3}}$dyne = $98 \times {10^{ - 8}}$ = F.
The formula of gravitational force between two masses m1 and m2 and the distance between them as r is,
F = $\dfrac{{G{m_1}{m_2}}}{{{r^2}}}$.
On putting the respective values we get the values of G as:
$ \Rightarrow G = \dfrac{{F{{(r)}^2}}}{{{m_1}{m_2}}} = \dfrac{{98 \times {{10}^{ - 8}} \times 0.2 \times 0.2}}{{40 \times 15}} = 6.53 \times {10^{ - 11}}$ .
Therefore the value of gravitational constant G here is $6.53 \times {10^{ - 11}}N{m^2}k{g^{ - 2}}$.
So, the correct answer is “Option B”.
Note:
Here one needs to know the conversion of units that is 1 dyne = ${10^{ - 5}}N$ and 1g weight = 980 dyne. Then we have done the conversion and used the formula of gravitational force between two bodies that is F = $\dfrac{{G{m_1}{m_2}}}{{{r^2}}}$. Knowing these things and proceeding like this will take you to the right answer.
Recently Updated Pages
Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Class 11 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

How much is 23 kg in pounds class 11 chemistry CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

What is the technique used to separate the components class 11 chemistry CBSE




