
The amplitude and time period of a simple harmonic oscillator are ‘a’ and ‘T’ respectively. The time taken by it in displacing from x=0 to x=$\dfrac{a}{2}$ will be
A. $T$
B. $\dfrac{T}{2}$
C. $\dfrac{T}{4}$
D. $\dfrac{T}{12}$
Answer
528.9k+ views
Hint: In order to find the time taken for displacement from $x=0$ to $x=\dfrac{a}{2}$, one has to know the equation of displacement of an SHM. We are also given the amplitude and time period as ‘a’ and ‘T’. We could substitute values of ‘x’, ‘a’ and ‘T’ in the equation of displacement of SHM and hence find time taken for required displacement in terms of time period T.
Formula used:
Equation of displacement of an SHM,
$x\left( t \right)=a\sin \left( \dfrac{2\pi }{T}t \right)$
Complete answer:
Let us understand the motion of a simple harmonic oscillator before solving the problem.
A simple harmonic oscillator oscillates in simple harmonic motion (SHM). A SHM, if you may recall, is a special type of periodic motion that obeys ‘Hooke’s law’, that is, the restoring force of any object executing SHM is directly proportional to its displacement magnitude and acts towards its equilibrium position. For better understanding, we consider the example of an object with mass ‘M’ attached to a spring on a frictionless surface, which indeed is a good example of SHM.
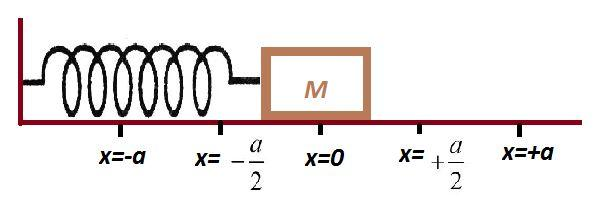
Here, we take x=0 as the object’s equilibrium position, that is, a position at which the net force is zero (the spring is neither stretched or compressed). If we were to stretch the object to position x=+a, (we could call that its amplitude, the maximum displacement from its equilibrium position) the object starts executing a SHM from x=+a to x=-a with a time period T (time taken for completing a full cycle of its periodic motion).
Displacement of an object executing SHM is a sinusoidal function of time. So, equation for position of object executing SHM as a function of time can be given by,
$x\left( t \right)=a\sin \left( \dfrac{2\pi }{T}t \right)$ ………… (1)
Now, in this question we are asked to find time taken to displace from x=0 to $x=\dfrac{a}{2}$ ,
Substituting $x=0$ in equation (1) gives,
$0=a\sin \left( \dfrac{2\pi }{T}t \right)$
$\sin \left( \dfrac{2\pi }{T}t \right)=0$
$t=0$
Substituting $x=\dfrac{a}{2}$ in equation (1) gives,
$\dfrac{a}{2}=a\sin \left( \dfrac{2\pi }{T}t \right)$
$\dfrac{2\pi }{T}\times t={{\sin }^{-1}}\left( \dfrac{1}{2} \right)$
$\dfrac{2\pi }{T}\times t=\dfrac{\pi }{6}$
$t=\dfrac{T}{12}$ …………….. (3)
Total time taken to displace from $x=0$ to $x=\dfrac{a}{2}$ is,
$t=\dfrac{T}{12}$
So, the correct answer is “Option D”.
Note:
We have to remember that t and T are very different from each other. ‘t’ is the time taken for the object to reach a certain location but T is the time period of a complete oscillation. The equation of displacement of SHM could be given in cosine terms too. In that case, we will not get t=0 at x=0, but you just have to subtract the terms accordingly from each other so that you only account for the time taken for the required displacement and then you will end up in the same answer.
Formula used:
Equation of displacement of an SHM,
$x\left( t \right)=a\sin \left( \dfrac{2\pi }{T}t \right)$
Complete answer:
Let us understand the motion of a simple harmonic oscillator before solving the problem.
A simple harmonic oscillator oscillates in simple harmonic motion (SHM). A SHM, if you may recall, is a special type of periodic motion that obeys ‘Hooke’s law’, that is, the restoring force of any object executing SHM is directly proportional to its displacement magnitude and acts towards its equilibrium position. For better understanding, we consider the example of an object with mass ‘M’ attached to a spring on a frictionless surface, which indeed is a good example of SHM.

Here, we take x=0 as the object’s equilibrium position, that is, a position at which the net force is zero (the spring is neither stretched or compressed). If we were to stretch the object to position x=+a, (we could call that its amplitude, the maximum displacement from its equilibrium position) the object starts executing a SHM from x=+a to x=-a with a time period T (time taken for completing a full cycle of its periodic motion).
Displacement of an object executing SHM is a sinusoidal function of time. So, equation for position of object executing SHM as a function of time can be given by,
$x\left( t \right)=a\sin \left( \dfrac{2\pi }{T}t \right)$ ………… (1)
Now, in this question we are asked to find time taken to displace from x=0 to $x=\dfrac{a}{2}$ ,
Substituting $x=0$ in equation (1) gives,
$0=a\sin \left( \dfrac{2\pi }{T}t \right)$
$\sin \left( \dfrac{2\pi }{T}t \right)=0$
$t=0$
Substituting $x=\dfrac{a}{2}$ in equation (1) gives,
$\dfrac{a}{2}=a\sin \left( \dfrac{2\pi }{T}t \right)$
$\dfrac{2\pi }{T}\times t={{\sin }^{-1}}\left( \dfrac{1}{2} \right)$
$\dfrac{2\pi }{T}\times t=\dfrac{\pi }{6}$
$t=\dfrac{T}{12}$ …………….. (3)
Total time taken to displace from $x=0$ to $x=\dfrac{a}{2}$ is,
$t=\dfrac{T}{12}$
So, the correct answer is “Option D”.
Note:
We have to remember that t and T are very different from each other. ‘t’ is the time taken for the object to reach a certain location but T is the time period of a complete oscillation. The equation of displacement of SHM could be given in cosine terms too. In that case, we will not get t=0 at x=0, but you just have to subtract the terms accordingly from each other so that you only account for the time taken for the required displacement and then you will end up in the same answer.
Recently Updated Pages
Physics and Measurement Mock Test 2025 – Practice Questions & Answers

NCERT Solutions For Class 5 English Marigold - The Little Bully

NCERT Solutions For Class 12 Maths Three Dimensional Geometry Exercise 11.1

NCERT Solutions For Class 11 English Woven Words (Poem) - Ajamil And The Tigers

NCERT Solutions For Class 6 Hindi Durva - Bhaaloo

NCERT Solutions For Class 12 Physics In Hindi - Wave Optics

Trending doubts
1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Proton was discovered by A Thomson B Rutherford C Chadwick class 11 chemistry CBSE

Draw a diagram of nephron and explain its structur class 11 biology CBSE




