
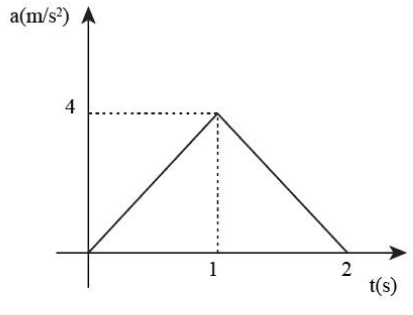
The acceleration time graph of a particle moving in a straight line is as shown in figure. The velocity of the particle at time \[t = 0\] is \[2\;{\rm{m/s}}\]. The velocity after \[2\;{\rm{s}}\] will be
A. \[6\;{\rm{m/s}}\]
B. \[4\;{\rm{m/s}}\]
C. \[2\;{\rm{m/s}}\]
D. \[8\;{\rm{m/s}}\]

Answer
515.1k+ views
Hint:The above problem is resolved by using the kinematic equation of motion. Moreover, the first kinematic equation of motion is used to resolve the problem. In the first kinematic equation of motion, the variables like the magnitude of initial velocity, the time interval, and the magnitude of acceleration can be identified by analysing the velocity-time graph. And by analysing this graph, the values are obtained. After obtaining the values, the substitution is made for the values to the mathematical equation of motion, and then the final answer is obtained.
Complete step by step answer:
Given:
The velocity at \[t = 0\] is, \[u = 2\;{\rm{m/s}}\].
The time interval is, \[t = 2\;{\rm{s}}\].
In order to find the velocity after 2 seconds, We need to find the area of the graph.
As, base represents the time and height represents the magnitude of acceleration \[a = 4\;{\rm{m/}}{{\rm{s}}^{\rm{2}}}\].
Then the area of the acceleration time graph is,
\[
v = 2 \times \left( {\dfrac{1}{2} \times t \times a} \right)\\
\Rightarrow v = 2 \times \left( {\dfrac{1}{2} \times 2\;{\rm{s}} \times 4\;{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\\
\therefore v = 8\;{\rm{m/s}}
\]
Therefore, the velocity after 2 seconds is \[8\;{\rm{m/s}}\] and option (D) is correct.
Note: To resolve the given problem, the concepts and applications of the kinematic equations of motion need to be taken under consideration and the various practical applications of the equations. While applying the kinematic equations of motion, one must always remember the increase or decrease of the variables' values. This is important because the sign conventions are decided by the increment and decrement of these variables' magnitude.
Complete step by step answer:
Given:
The velocity at \[t = 0\] is, \[u = 2\;{\rm{m/s}}\].
The time interval is, \[t = 2\;{\rm{s}}\].
In order to find the velocity after 2 seconds, We need to find the area of the graph.
As, base represents the time and height represents the magnitude of acceleration \[a = 4\;{\rm{m/}}{{\rm{s}}^{\rm{2}}}\].
Then the area of the acceleration time graph is,
\[
v = 2 \times \left( {\dfrac{1}{2} \times t \times a} \right)\\
\Rightarrow v = 2 \times \left( {\dfrac{1}{2} \times 2\;{\rm{s}} \times 4\;{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\\
\therefore v = 8\;{\rm{m/s}}
\]
Therefore, the velocity after 2 seconds is \[8\;{\rm{m/s}}\] and option (D) is correct.
Note: To resolve the given problem, the concepts and applications of the kinematic equations of motion need to be taken under consideration and the various practical applications of the equations. While applying the kinematic equations of motion, one must always remember the increase or decrease of the variables' values. This is important because the sign conventions are decided by the increment and decrement of these variables' magnitude.
Recently Updated Pages
Physics and Measurement Mock Test 2025 – Practice Questions & Answers

NCERT Solutions For Class 5 English Marigold - The Little Bully

NCERT Solutions For Class 12 Maths Three Dimensional Geometry Exercise 11.1

NCERT Solutions For Class 11 English Woven Words (Poem) - Ajamil And The Tigers

NCERT Solutions For Class 6 Hindi Durva - Bhaaloo

NCERT Solutions For Class 12 Physics In Hindi - Wave Optics

Trending doubts
1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Proton was discovered by A Thomson B Rutherford C Chadwick class 11 chemistry CBSE

Draw a diagram of nephron and explain its structur class 11 biology CBSE




