
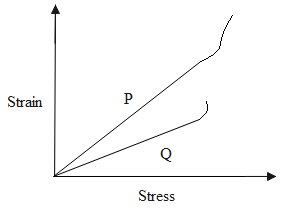
In plotting stress versus strain curves for two materials P and Q, a student by mistake puts a strain on the y-axis and stress on the x-axis as shown in the figure. Then the correct statements(s) is (are)
A. P has more tensile strength than Q
B. P is more ductile than Q
C. P is more brittle than Q
D. The Young’s modulus of P is more than that of Q

Answer
482.4k+ views
Hint: The stress-strain curve for a material gives the slope equal to that of Young’s modulus of that material. And, the slope is the angle of tan function. Even the modulus of rigidity can be defined using this slope. So, using these terms, we will answer this question.
Formula used: \[Y=\dfrac{Stress}{Strain}\]
Complete step by step answer:
The stress-strain curve for a material gives the slope equal to that of Young’s modulus of that material. And, the slope is the angle of tan function.
\[Y=\dfrac{Stress}{Strain}\]
More the Young’s modulus more will be the tensile strength.
As Young’s modulus of the material Q is more than that of the material P, thus, the tensile strength of Q is more than that of the material P.
The modulus of rigidity is the ratio of the tangential stress to the shearing strain. The formula that defines the relationship between the modulus of rigidity, stress and strain is given as follows.
\[\eta =\dfrac{Stress}{Strain}\]
Where \[\eta \] is the modulus of rigidity.
Considering a particle value of stress and strain, we get to know that, the stress of the material P is more than that of the material Q. Thus, the length of the material P can be increased by a larger amount than Q, for the same amount of applied strain. Therefore, we can say that the material P is more ductile than the material Q. And at the same time, we can say that, the material P is less brittle than the material Q, because, P elongates more before it breaks than Q.
\[\Rightarrow {{Y}_{Q}}>{{Y}_{P}}\]
So, the correct answer is “Option B”.
Note: This is neither a tricky nor simple question. The curves are drawn to make the question a bit complicated. We only need the value of the slope of the angle made by the stress-strain curve to solve this type of question.
Formula used: \[Y=\dfrac{Stress}{Strain}\]
Complete step by step answer:
The stress-strain curve for a material gives the slope equal to that of Young’s modulus of that material. And, the slope is the angle of tan function.
\[Y=\dfrac{Stress}{Strain}\]
More the Young’s modulus more will be the tensile strength.
As Young’s modulus of the material Q is more than that of the material P, thus, the tensile strength of Q is more than that of the material P.
The modulus of rigidity is the ratio of the tangential stress to the shearing strain. The formula that defines the relationship between the modulus of rigidity, stress and strain is given as follows.
\[\eta =\dfrac{Stress}{Strain}\]
Where \[\eta \] is the modulus of rigidity.
Considering a particle value of stress and strain, we get to know that, the stress of the material P is more than that of the material Q. Thus, the length of the material P can be increased by a larger amount than Q, for the same amount of applied strain. Therefore, we can say that the material P is more ductile than the material Q. And at the same time, we can say that, the material P is less brittle than the material Q, because, P elongates more before it breaks than Q.
\[\Rightarrow {{Y}_{Q}}>{{Y}_{P}}\]
So, the correct answer is “Option B”.
Note: This is neither a tricky nor simple question. The curves are drawn to make the question a bit complicated. We only need the value of the slope of the angle made by the stress-strain curve to solve this type of question.
Recently Updated Pages
Division Facts Worksheets: Fast Maths Drills for Grades 2-5

Math Drills Division Worksheets | Free Printable PDF Practice

Class 1 Antonyms Worksheet: Printable Opposite Words Practice

NCERT Solutions For Class 4 English Marigold (Poem) - The Watering Rhyme And The Donkey

Kindergarten Tracing Letter T Worksheet – Free Printable PDF

Sets, Relations, and Functions Mock Test 2025-26

Trending doubts
1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Proton was discovered by A Thomson B Rutherford C Chadwick class 11 chemistry CBSE

Draw a diagram of nephron and explain its structur class 11 biology CBSE




