
In a school, there are $3$ types of games to be played. Some of the students play $2$ types of games, but none play all $3$ games. Which Venn diagrams can justify the above statements?
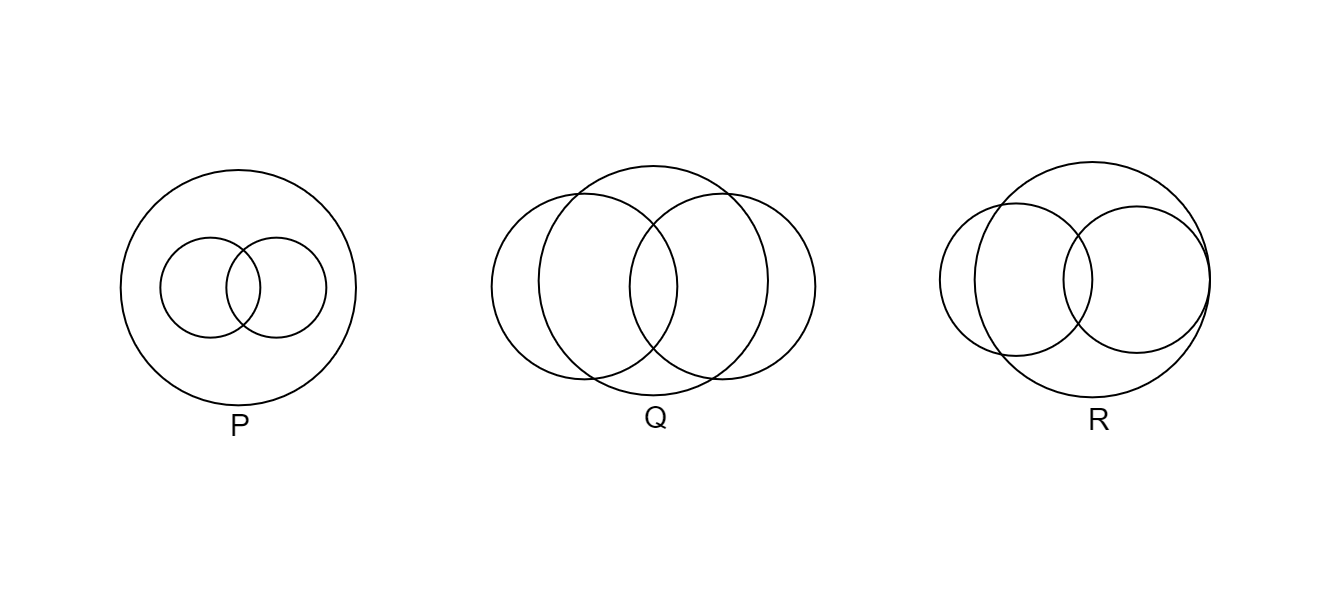
1. P and R
2. P and Q
3. None of these
4. Q and R
Answer
162.9k+ views
Hint: Here, we are given three Venn diagrams P, Q, and R. We have to select which of the diagram justifies the statement that some students play two games, but none plays all three games. It means, we have to check which of the diagram is not of intersection.
Formula Used:
Given Venn diagram are of intersection i.e., $A \cap B \cap C$
Complete step by step Solution:
Let, A, B, and C be the first, second, and third games that are played by the student in school
Now, let the condition be some students play two games, but none play all three games.
It means, in the Venn diagram there should be no common part in all three games.
There should be a common part in any of the two games,
Case 1: A and B
Case 2: B and C
Case 3: A and C
A Venn diagram of the given statement is attached below,
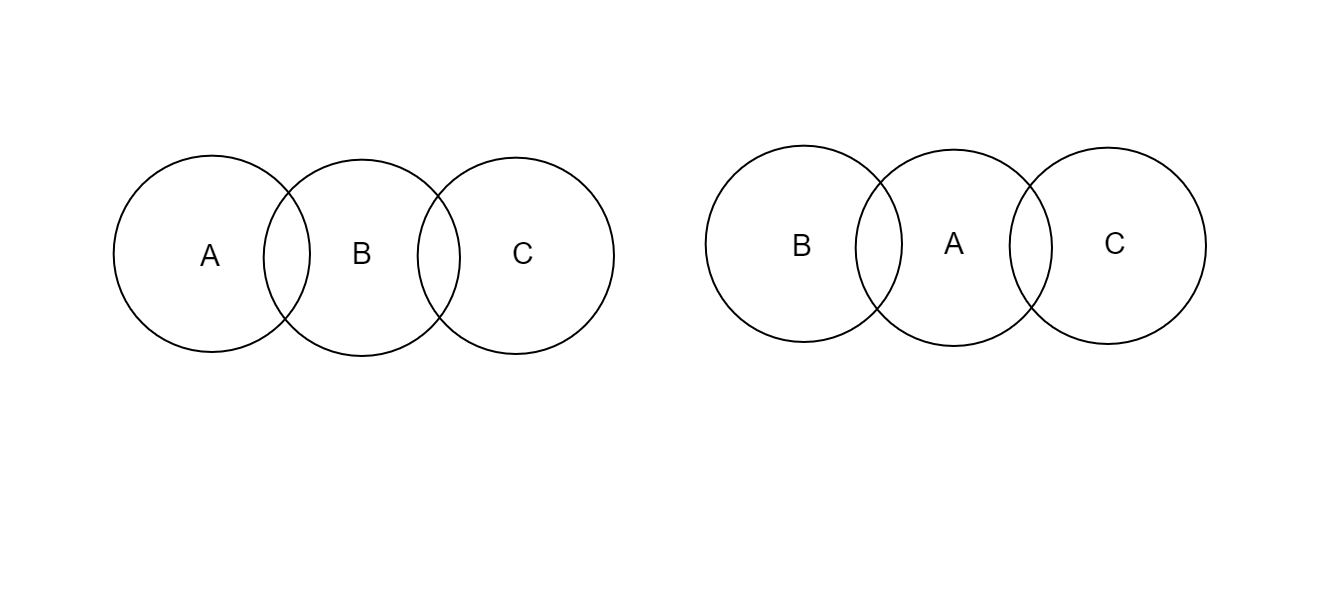 Now, in the given Venn diagram P, Q, and R, there are common parts in all three games. This implies that there are some students who play all three games which contradicts the statement that none of the students plays all three games.
Now, in the given Venn diagram P, Q, and R, there are common parts in all three games. This implies that there are some students who play all three games which contradicts the statement that none of the students plays all three games.
Hence, the correct option is 3.
Note: The key concept involved in solving this problem is a good knowledge of Union and Intersection. Students must know that the union of two sets P and Q corresponds to the set of elements that are included in set P, set Q, or both sets P and Q. The intersection of two subsets of the universal set U, A, and B, is the set that contains all of the elements that are shared by both A and B.
Formula Used:
Given Venn diagram are of intersection i.e., $A \cap B \cap C$
Complete step by step Solution:
Let, A, B, and C be the first, second, and third games that are played by the student in school
Now, let the condition be some students play two games, but none play all three games.
It means, in the Venn diagram there should be no common part in all three games.
There should be a common part in any of the two games,
Case 1: A and B
Case 2: B and C
Case 3: A and C
A Venn diagram of the given statement is attached below,
 Now, in the given Venn diagram P, Q, and R, there are common parts in all three games. This implies that there are some students who play all three games which contradicts the statement that none of the students plays all three games.
Now, in the given Venn diagram P, Q, and R, there are common parts in all three games. This implies that there are some students who play all three games which contradicts the statement that none of the students plays all three games.Hence, the correct option is 3.
Note: The key concept involved in solving this problem is a good knowledge of Union and Intersection. Students must know that the union of two sets P and Q corresponds to the set of elements that are included in set P, set Q, or both sets P and Q. The intersection of two subsets of the universal set U, A, and B, is the set that contains all of the elements that are shared by both A and B.
Recently Updated Pages
Geometry of Complex Numbers – Topics, Reception, Audience and Related Readings

JEE Main 2021 July 25 Shift 1 Question Paper with Answer Key

JEE Main 2021 July 22 Shift 2 Question Paper with Answer Key

JEE Main 2025 Session 2: Exam Date, Admit Card, Syllabus, & More

JEE Atomic Structure and Chemical Bonding important Concepts and Tips

JEE Amino Acids and Peptides Important Concepts and Tips for Exam Preparation

Trending doubts
Degree of Dissociation and Its Formula With Solved Example for JEE

Instantaneous Velocity - Formula based Examples for JEE

JEE Main Chemistry Question Paper with Answer Keys and Solutions

JEE Main Reservation Criteria 2025: SC, ST, EWS, and PwD Candidates

What is Normality in Chemistry?

Chemistry Electronic Configuration of D Block Elements: JEE Main 2025

Other Pages
NCERT Solutions for Class 11 Maths Chapter 6 Permutations and Combinations

NCERT Solutions for Class 11 Maths Chapter 8 Sequences and Series

Total MBBS Seats in India 2025: Government College Seat Matrix

NEET Total Marks 2025: Important Information and Key Updates

Neet Cut Off 2025 for MBBS in Tamilnadu: AIQ & State Quota Analysis

Karnataka NEET Cut off 2025 - Category Wise Cut Off Marks




