
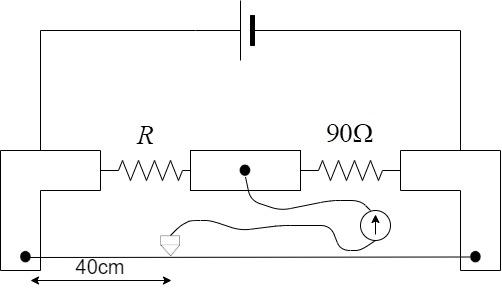
During an experiment with the metre bridge, the galvanometer shows a null point when the jockey is pressed at $40.0$ $cm$ using a standard resistance of $90\Omega $ as shown in the figure. The least count of the scale used in the meter bridge is 1mm. The unknown resistance is:
A) $60 \pm 0.15\Omega $
B) $135 \pm 0.56\Omega $
C) $60 \pm 0.25\Omega $
D) $135 \pm 0.23\Omega $
Answer
180.3k+ views
Hint: The Metre Bridge is an arrangement derived from the Wheatstone’s network. The Wheatstone’s network is an arrangement of 4 resistors as shown:
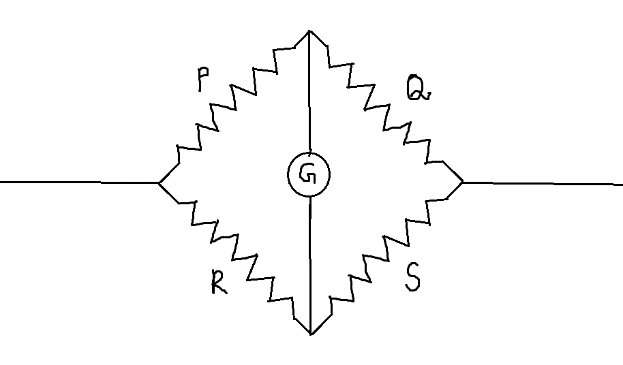
The Wheatstone’s network is said to be balanced if the reading in the galvanometer becomes zero. This condition is possible when –
$\dfrac{P}{Q} = \dfrac{R}{S}$
Complete step by step answer:
Step 1: Calculating the unknown resistance.
In a meter bridge, the ratio of the known resistance to the unknown resistance is equal to the ratio of the corresponding lengths.
If the galvanometer reading turns 0 when the jockey is pressed at a length $l$, the formula for finding the unknown resistance R –
$\dfrac{R}{S} = \dfrac{l}{{1 - l}}$
where S – known resistance.
In this problem,
$
\Rightarrow S = 90\Omega \\
\Rightarrow l = 40cm = 0.4m \\
$
Hence, substitute these values to obtain the unknown resistance R –
$
\Rightarrow \dfrac{R}{S} = \dfrac{l}{{1 - l}} \\
\Rightarrow R = S\dfrac{l}{{1 - l}} \\
Solving, \\
\Rightarrow R = 90\dfrac{{0.4}}{{1 - 0.4}} \\
\Rightarrow R = 90\dfrac{{0.4}}{{0.6}} = 60\Omega \\
$
Step 2: Finding the change in resistance
Let us consider the equation for unknown resistance in the meter bridge
$R = S\dfrac{l}{{1 - l}}$
To find the incremental value of change in resistance, we need to differentiate the equation with respect to length
$
\Rightarrow \dfrac{{dR}}{{dl}} = R\left( {\dfrac{1}{l} + \dfrac{1}{{1 - l}}} \right) \\
rearranging, \\
\Rightarrow \dfrac{{dR}}{R} = \dfrac{{dl}}{l} + \dfrac{{dl}}{{1 - l}} \\
$
Least count,$dl = 1mm = 0.001m$
Substituting in the formula, we get:
$
\Rightarrow \dfrac{{dR}}{R} = \dfrac{{dl}}{l} + \dfrac{{dl}}{{1 - l}} \\
\Rightarrow \dfrac{{dR}}{R} = \dfrac{{0.001}}{{0.4}} + \dfrac{{0.001}}{{1 - 0.4}} \\
\Rightarrow \dfrac{{dR}}{R} = \dfrac{{0.001}}{{0.4}} + \dfrac{{0.001}}{{0.6}} = \dfrac{{0.01}}{4} + \dfrac{{0.01}}{6} \\
\Rightarrow \dfrac{{dR}}{R} = 0.25\Omega \\
$
Hence, incremental change = $ \pm 0.25\Omega $
Hence, the correct option is Option C, $60 \pm 0.25\Omega.$
Note: Students can, often, get confused between R and S in the formula. Always, note that the known resistance will be in the denominator as it is connected on the left. So, the known resistance S will be equivalent to (1-l).

The Wheatstone’s network is said to be balanced if the reading in the galvanometer becomes zero. This condition is possible when –
$\dfrac{P}{Q} = \dfrac{R}{S}$
Complete step by step answer:
Step 1: Calculating the unknown resistance.
In a meter bridge, the ratio of the known resistance to the unknown resistance is equal to the ratio of the corresponding lengths.
If the galvanometer reading turns 0 when the jockey is pressed at a length $l$, the formula for finding the unknown resistance R –
$\dfrac{R}{S} = \dfrac{l}{{1 - l}}$
where S – known resistance.
In this problem,
$
\Rightarrow S = 90\Omega \\
\Rightarrow l = 40cm = 0.4m \\
$
Hence, substitute these values to obtain the unknown resistance R –
$
\Rightarrow \dfrac{R}{S} = \dfrac{l}{{1 - l}} \\
\Rightarrow R = S\dfrac{l}{{1 - l}} \\
Solving, \\
\Rightarrow R = 90\dfrac{{0.4}}{{1 - 0.4}} \\
\Rightarrow R = 90\dfrac{{0.4}}{{0.6}} = 60\Omega \\
$
Step 2: Finding the change in resistance
Let us consider the equation for unknown resistance in the meter bridge
$R = S\dfrac{l}{{1 - l}}$
To find the incremental value of change in resistance, we need to differentiate the equation with respect to length
$
\Rightarrow \dfrac{{dR}}{{dl}} = R\left( {\dfrac{1}{l} + \dfrac{1}{{1 - l}}} \right) \\
rearranging, \\
\Rightarrow \dfrac{{dR}}{R} = \dfrac{{dl}}{l} + \dfrac{{dl}}{{1 - l}} \\
$
Least count,$dl = 1mm = 0.001m$
Substituting in the formula, we get:
$
\Rightarrow \dfrac{{dR}}{R} = \dfrac{{dl}}{l} + \dfrac{{dl}}{{1 - l}} \\
\Rightarrow \dfrac{{dR}}{R} = \dfrac{{0.001}}{{0.4}} + \dfrac{{0.001}}{{1 - 0.4}} \\
\Rightarrow \dfrac{{dR}}{R} = \dfrac{{0.001}}{{0.4}} + \dfrac{{0.001}}{{0.6}} = \dfrac{{0.01}}{4} + \dfrac{{0.01}}{6} \\
\Rightarrow \dfrac{{dR}}{R} = 0.25\Omega \\
$
Hence, incremental change = $ \pm 0.25\Omega $
Hence, the correct option is Option C, $60 \pm 0.25\Omega.$
Note: Students can, often, get confused between R and S in the formula. Always, note that the known resistance will be in the denominator as it is connected on the left. So, the known resistance S will be equivalent to (1-l).
Recently Updated Pages
Uniform Acceleration - Definition, Equation, Examples, and FAQs

Difference Between Mass and Weight

JEE Main 2023 April 13 Shift 2 Question Paper with Answer Key

JEE Main 2023 April 11 Shift 2 Question Paper with Answer Key

JEE Main 2023 April 10 Shift 2 Question Paper with Answer Key

JEE Main 2023 (April 8th Shift 2) Physics Question Paper with Answer Key

Trending doubts
Electric field due to uniformly charged sphere class 12 physics JEE_Main

Atomic Structure - Electrons, Protons, Neutrons and Atomic Models

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Degree of Dissociation and Its Formula With Solved Example for JEE

Two cells of emf 4V and 2V and internal resistance class 12 physics JEE_Main

Current Loop as Magnetic Dipole and Its Derivation for JEE

Other Pages
Formula for number of images formed by two plane mirrors class 12 physics JEE_Main

JEE Main Chemistry Question Paper with Answer Keys and Solutions

JEE Advanced 2026 Notes

Diffraction of Light - Young’s Single Slit Experiment

A conducting wire is bent in the form of a parabola class 12 physics JEE_Main

JEE Advanced 2025 Revision Notes for Practical Organic Chemistry




