
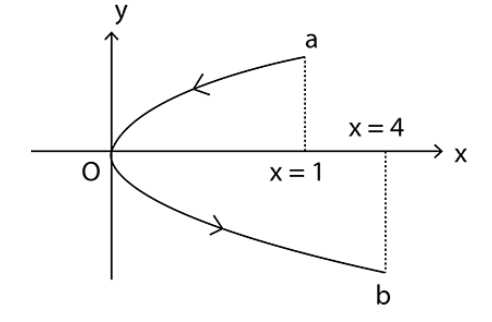
A conducting wire is bent in the form of a parabola ${{\text{y}}^2} = {\text{x}}$ carrying a current ${\text{i}} = 1\;{\text{A}}$ as shown in the figure. This wire is placed in a magnetic field $\overrightarrow {\text{B}} = - 2\widehat {\text{k}}$ \[T\] . The unit vector in the direction of force (on the given portion a to b) is:
(A) $\dfrac{{3i + 4j}}{5}$
(B) $\dfrac{{i + j}}{{\sqrt 2 }}$
(C) $\dfrac{{i + 2j}}{{\sqrt 5 }}$
(D) $\dfrac{{i - 2j}}{{\sqrt 5 }}$
Answer
180k+ views
Hint: A magnetic field has magnitude as well as direction. It is a vector quantity, therefore, and is denoted by $\vec B$. A current-carrying conductor's magnetic field depends on the current in the conductor and the distance of the point from the conductor. The magnetic field's direction is perpendicular to the wire.
Formula Used: We will use the following formula to find out the required force
$\vec F = i(\vec L \times \vec B)$
Where
$\overrightarrow {\text{F}} $ is the force vector
${\text{i}}$ is the current across the conducting wire
$\overrightarrow {\text{L}} $ is the length of the wire in vector form
$\overrightarrow {\text{B}} $ is the magnetic field represented in vector form
Complete Step-by-Step Solution:
According to the question, the following information is provided to us
The equation of the parabola is ${y^2} = x$
The electrical current flowing in the conducting wire is $i = 1A$
The magnetic field $\vec B = - 2\hat kT$
The coordinates of point $a(1,1)$
The coordinates of point $b(4, - 2)$
Now we need to calculate $\overrightarrow {\text{L}} $
So, we get
$\vec L = (4 - 1)\hat i + ( - 2 - 1)\hat j$
Upon further solving, we get
$\vec L = 3\hat i - 3\hat j$
Now, we know that
$\vec F = i(\vec L \times \vec B)$
Now, we will put the known values in to the above formula to get the force vector
\[\vec F = 1((3\hat i - 3\hat j) \times - 2\hat k)\]
Upon further solving, we get
\[\vec F = 6\hat j + 6\hat i\]
Now, we have to calculate the magnitude of the force vector, that is
$|\overrightarrow {\text{F}} | = |6\widehat {\text{j}} + 6\widehat {\text{i}}| = 6\sqrt 2 $
Now, we have to calculate the unit vector of force, which can be obtained by
$\widehat {\text{F}} = \dfrac{{\overrightarrow {\text{F}} }}{{|\overrightarrow {\text{F}} |}}$
Upon substituting the value of force vector, we get
$\hat F = \dfrac{{6\widehat {\text{j}} + 6\widehat {\text{i}}}}{{6\sqrt 2 }}$
Upon further solving, we get the unit vector of force as
$\therefore \hat F = \dfrac{{\widehat {\text{i}} + \widehat {\text{j}}}}{{\sqrt 2 }}$
Hence, the correct option is (B.)
Note: As vector quantities, the physical quantities for which both magnitude and direction are distinctly defined are known. By putting an arrow over the denotations representing them, vectors are denoted. For example, to define a vehicle's acceleration, its direction must also be specified along with its magnitude. It can be represented as $\vec am/{s^2}$ in vector form. Vectors can be easily represented in three dimensions using the coordinate system.
Formula Used: We will use the following formula to find out the required force
$\vec F = i(\vec L \times \vec B)$
Where
$\overrightarrow {\text{F}} $ is the force vector
${\text{i}}$ is the current across the conducting wire
$\overrightarrow {\text{L}} $ is the length of the wire in vector form
$\overrightarrow {\text{B}} $ is the magnetic field represented in vector form
Complete Step-by-Step Solution:
According to the question, the following information is provided to us
The equation of the parabola is ${y^2} = x$
The electrical current flowing in the conducting wire is $i = 1A$
The magnetic field $\vec B = - 2\hat kT$
The coordinates of point $a(1,1)$
The coordinates of point $b(4, - 2)$
Now we need to calculate $\overrightarrow {\text{L}} $
So, we get
$\vec L = (4 - 1)\hat i + ( - 2 - 1)\hat j$
Upon further solving, we get
$\vec L = 3\hat i - 3\hat j$
Now, we know that
$\vec F = i(\vec L \times \vec B)$
Now, we will put the known values in to the above formula to get the force vector
\[\vec F = 1((3\hat i - 3\hat j) \times - 2\hat k)\]
Upon further solving, we get
\[\vec F = 6\hat j + 6\hat i\]
Now, we have to calculate the magnitude of the force vector, that is
$|\overrightarrow {\text{F}} | = |6\widehat {\text{j}} + 6\widehat {\text{i}}| = 6\sqrt 2 $
Now, we have to calculate the unit vector of force, which can be obtained by
$\widehat {\text{F}} = \dfrac{{\overrightarrow {\text{F}} }}{{|\overrightarrow {\text{F}} |}}$
Upon substituting the value of force vector, we get
$\hat F = \dfrac{{6\widehat {\text{j}} + 6\widehat {\text{i}}}}{{6\sqrt 2 }}$
Upon further solving, we get the unit vector of force as
$\therefore \hat F = \dfrac{{\widehat {\text{i}} + \widehat {\text{j}}}}{{\sqrt 2 }}$
Hence, the correct option is (B.)
Note: As vector quantities, the physical quantities for which both magnitude and direction are distinctly defined are known. By putting an arrow over the denotations representing them, vectors are denoted. For example, to define a vehicle's acceleration, its direction must also be specified along with its magnitude. It can be represented as $\vec am/{s^2}$ in vector form. Vectors can be easily represented in three dimensions using the coordinate system.
Recently Updated Pages
Degree of Dissociation Important Concepts and Tips for JEE

JEE Main Chemistry Question Paper PDF Download with Answer Key

JEE Electricity and Magnetism Important Concepts and Tips for Exam Preparation

JEE Energetics Important Concepts and Tips for Exam Preparation

JEE Isolation, Preparation and Properties of Non-metals Important Concepts and Tips for Exam Preparation

States of Matter Chapter For JEE Main Chemistry

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Displacement-Time Graph and Velocity-Time Graph for JEE

Electric field due to uniformly charged sphere class 12 physics JEE_Main

Atomic Structure - Electrons, Protons, Neutrons and Atomic Models

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

What is Hybridisation in Chemistry?

JEE Main 2025: Conversion of Galvanometer Into Ammeter And Voltmeter in Physics

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

Wheatstone Bridge for JEE Main Physics 2025

Electric Field Due to Uniformly Charged Ring for JEE Main 2025 - Formula and Derivation




