
Two cells of emf \[4V\] and \[2V\], and internal resistance \[2\Omega \] and \[1\Omega \] respectively are connected in parallel so as to send the current in the same direction through an external resistance of \[10\Omega \]. Find the potential difference across the \[10\Omega \] resistor.
Answer
197.4k+ views
Hint: The given problem is an example of grouping of two cells in parallel. Two cells are said to be connected in parallel between two points, if positive terminals of both the cells are connected to the one point and negative terminals of both the cells are connected to the other point.
Complete step by step solution:
Step 1:
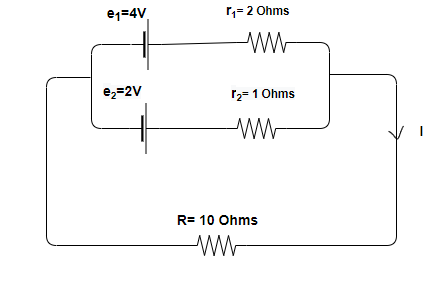
As shown in the above circuit, emfs of the given cells are \[\mathop e\nolimits_1 \] and \[\mathop e\nolimits_2 \] respectively. And internal resistances of these given cells are \[\mathop r\nolimits_1 \] and \[\mathop r\nolimits_2 \] respectively.
Let the current flowing in the circuit because of the combination of these cells is \[I\] .
Where \[\mathop e\nolimits_1 = 4V\], \[\mathop e\nolimits_2 = 2V\], \[\mathop r\nolimits_1 = 2\Omega \] , and \[\mathop r\nolimits_2 = 1\Omega \].
And the external resistance is given by \[R = 10\Omega \].
Step 2:
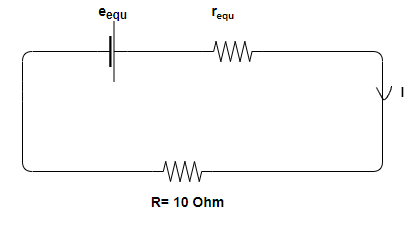
As shown in the above figure that the given circuit in step 1 that is a parallel combination of two cells can be replaced by a single cell of equivalent emf of \[\mathop e\nolimits_{equ} \] between the two given points and internal resistance that is equivalent resistance \[\mathop r\nolimits_{equ} \].
For the given circuit \[\mathop r\nolimits_{equ} \] can be calculated by the formula –
\[\mathop r\nolimits_{equ} = \dfrac{{\mathop r\nolimits_1 \mathop r\nolimits_2 }}{{\mathop r\nolimits_1 + \mathop r\nolimits_2 }}\]; putting the values of \[\mathop r\nolimits_1 \] and \[\mathop r\nolimits_2 \] in this equation
\[\mathop r\nolimits_{equ} = \dfrac{{2 \times 1}}{{2 + 1}}\]
\[\mathop r\nolimits_{equ} = \dfrac{2}{3}\Omega \]..................(1)
We know that the relationship between voltage \[V\], total current \[I\], and resistance \[R\] is given by Ohm's Law i.e., . So, using this relationship for the same given circuit \[\mathop e\nolimits_{equ} \] (i.e., voltage \[V\] ) can be calculated by the formula –
\[\mathop e\nolimits_{equ} = \left( {\dfrac{{\mathop e\nolimits_1 }}{{\mathop r\nolimits_1 }} + \dfrac{{\mathop e\nolimits_2 }}{{\mathop r\nolimits_2 }}} \right)\mathop r\nolimits_{equ} \]; putting the values of \[\mathop e\nolimits_1 \] and \[\mathop e\nolimits_2 \] , and \[\mathop r\nolimits_{equ} \] in this equation
\[\mathop e\nolimits_{equ} = \left( {\dfrac{4}{2} + \dfrac{2}{1}} \right)\dfrac{2}{3}\]
\[\mathop e\nolimits_{equ} = \dfrac{8}{3}V\]...................(2)
Step 3: Now potential difference across the \[R = 10\Omega \] (let \[\mathop E\nolimits_R \]) can be calculated by voltage divider rule as given follows –
\[\mathop E\nolimits_R = \left( {\dfrac{R}{{R + \mathop r\nolimits_{equ} }}} \right)\mathop e\nolimits_{equ} \]
Now, using the values of \[\mathop e\nolimits_{equ} \], \[\mathop r\nolimits_{equ} \], and \[R\] from above calculations, we will get
\[\mathop E\nolimits_R = \left( {\dfrac{10}{{10 + {2/3}}}} \right)\dfrac{8}{3}\]
\[\mathop E\nolimits_R = \left( {\dfrac{{10 \times 3}}{{30 + 2}}} \right)\dfrac{8}{3}\]; on simplifying the above equation
\[\mathop E\nolimits_R = \dfrac{{10 \times 8}}{{32}}\]
\[\mathop E\nolimits_R = 2.5V\]
The potential difference across the given resistance \[R = 10\Omega \] is \[\mathop E\nolimits_R = 2.5V\].
Note: If \[n\] number of identical cells are connected in parallel of emfs \[e\] and internal resistance \[r\], then internal equivalent resistance is given by –
\[\mathop r\nolimits_{equ} = \dfrac{r}{n}\].
In a parallel combination of identical cells, the effective /equivalent emf in the circuit is equal to the emf due to a single cell i.e., \[\mathop e\nolimits_{equ} = e\].
Complete step by step solution:
Step 1:

As shown in the above circuit, emfs of the given cells are \[\mathop e\nolimits_1 \] and \[\mathop e\nolimits_2 \] respectively. And internal resistances of these given cells are \[\mathop r\nolimits_1 \] and \[\mathop r\nolimits_2 \] respectively.
Let the current flowing in the circuit because of the combination of these cells is \[I\] .
Where \[\mathop e\nolimits_1 = 4V\], \[\mathop e\nolimits_2 = 2V\], \[\mathop r\nolimits_1 = 2\Omega \] , and \[\mathop r\nolimits_2 = 1\Omega \].
And the external resistance is given by \[R = 10\Omega \].
Step 2:

As shown in the above figure that the given circuit in step 1 that is a parallel combination of two cells can be replaced by a single cell of equivalent emf of \[\mathop e\nolimits_{equ} \] between the two given points and internal resistance that is equivalent resistance \[\mathop r\nolimits_{equ} \].
For the given circuit \[\mathop r\nolimits_{equ} \] can be calculated by the formula –
\[\mathop r\nolimits_{equ} = \dfrac{{\mathop r\nolimits_1 \mathop r\nolimits_2 }}{{\mathop r\nolimits_1 + \mathop r\nolimits_2 }}\]; putting the values of \[\mathop r\nolimits_1 \] and \[\mathop r\nolimits_2 \] in this equation
\[\mathop r\nolimits_{equ} = \dfrac{{2 \times 1}}{{2 + 1}}\]
\[\mathop r\nolimits_{equ} = \dfrac{2}{3}\Omega \]..................(1)
We know that the relationship between voltage \[V\], total current \[I\], and resistance \[R\] is given by Ohm's Law i.e., . So, using this relationship for the same given circuit \[\mathop e\nolimits_{equ} \] (i.e., voltage \[V\] ) can be calculated by the formula –
\[\mathop e\nolimits_{equ} = \left( {\dfrac{{\mathop e\nolimits_1 }}{{\mathop r\nolimits_1 }} + \dfrac{{\mathop e\nolimits_2 }}{{\mathop r\nolimits_2 }}} \right)\mathop r\nolimits_{equ} \]; putting the values of \[\mathop e\nolimits_1 \] and \[\mathop e\nolimits_2 \] , and \[\mathop r\nolimits_{equ} \] in this equation
\[\mathop e\nolimits_{equ} = \left( {\dfrac{4}{2} + \dfrac{2}{1}} \right)\dfrac{2}{3}\]
\[\mathop e\nolimits_{equ} = \dfrac{8}{3}V\]...................(2)
Step 3: Now potential difference across the \[R = 10\Omega \] (let \[\mathop E\nolimits_R \]) can be calculated by voltage divider rule as given follows –
\[\mathop E\nolimits_R = \left( {\dfrac{R}{{R + \mathop r\nolimits_{equ} }}} \right)\mathop e\nolimits_{equ} \]
Now, using the values of \[\mathop e\nolimits_{equ} \], \[\mathop r\nolimits_{equ} \], and \[R\] from above calculations, we will get
\[\mathop E\nolimits_R = \left( {\dfrac{10}{{10 + {2/3}}}} \right)\dfrac{8}{3}\]
\[\mathop E\nolimits_R = \left( {\dfrac{{10 \times 3}}{{30 + 2}}} \right)\dfrac{8}{3}\]; on simplifying the above equation
\[\mathop E\nolimits_R = \dfrac{{10 \times 8}}{{32}}\]
\[\mathop E\nolimits_R = 2.5V\]
The potential difference across the given resistance \[R = 10\Omega \] is \[\mathop E\nolimits_R = 2.5V\].
Note: If \[n\] number of identical cells are connected in parallel of emfs \[e\] and internal resistance \[r\], then internal equivalent resistance is given by –
\[\mathop r\nolimits_{equ} = \dfrac{r}{n}\].
In a parallel combination of identical cells, the effective /equivalent emf in the circuit is equal to the emf due to a single cell i.e., \[\mathop e\nolimits_{equ} = e\].
Recently Updated Pages
JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

Geostationary vs Geosynchronous Satellites: Definitions, Differences, Uses

Complex Numbers - Important Concepts and Tips for JEE

JEE Main 2023 (February 1st Shift 2) Maths Question Paper with Answer Key

JEE Main 2022 (July 25th Shift 2) Physics Question Paper with Answer Key

Inertial and Non-Inertial Frame of Reference: Definition, Differences & Examples

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

Equation of Trajectory in Projectile Motion: Derivation & Proof

Atomic Structure: Definition, Models, and Examples

Hybridisation in Chemistry – Concept, Types & Applications

Angle of Deviation in a Prism – Formula, Diagram & Applications

Collision: Meaning, Types & Examples in Physics

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

How to Convert a Galvanometer into an Ammeter or Voltmeter

Average and RMS Value in Physics: Formula, Comparison & Application

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Formula for number of images formed by two plane mirrors class 12 physics JEE_Main




