
A 110kg panda is riding on a 3.0m long swing whose mass can be considered negligible. The highest point of its arc occurs when the swing makes a ${{20}^{\circ }}$ angle with the vertical.
What is the magnitude of the total tension in the ropes of the swing at that point?
A: 0 N
B: 103 N
C: 369 N
D: 1013 N
E: 1078 N
Answer
521.7k+ views
Hint: This is an example of motion in a vertical circle as the panda completes arcs in the swing. The total tension is the required force here. All the necessary forces can be considered by constructing a free body diagram according to the given criterion.
Step by step answer: We are given that the mass of the panda is 110kg and the highest point of the swing occurs when it forms ${{20}^{\circ }}$with the vertical. With the given conditions, we can construct a free body diagram of the question and identify the forces acting in the system.
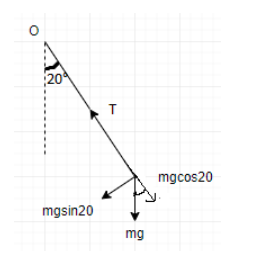
In the free body diagram, we have resolved the gravitational force into its horizontal and vertical components in accordance with the angle $\theta ={{20}^{\circ }}$
From, figure, we can infer that the tension acts opposite to the horizontal component of gravitational force.
Thus,
$
T=mg\cos 20 \\
\therefore T=110\times 9.8\times 0.94=1013N \\
$
Hence, option D is the correct answer among the given options.
Note: While solving such questions the most crucial thing is to draw the free body diagram correctly.Free body diagram is defined as a graphical illustration or the representation of all the forces that are applied. It also includes the moments and the resultants. It is helpful to solve both simple and complex problems in mechanics.
Step by step answer: We are given that the mass of the panda is 110kg and the highest point of the swing occurs when it forms ${{20}^{\circ }}$with the vertical. With the given conditions, we can construct a free body diagram of the question and identify the forces acting in the system.

In the free body diagram, we have resolved the gravitational force into its horizontal and vertical components in accordance with the angle $\theta ={{20}^{\circ }}$
From, figure, we can infer that the tension acts opposite to the horizontal component of gravitational force.
Thus,
$
T=mg\cos 20 \\
\therefore T=110\times 9.8\times 0.94=1013N \\
$
Hence, option D is the correct answer among the given options.
Note: While solving such questions the most crucial thing is to draw the free body diagram correctly.Free body diagram is defined as a graphical illustration or the representation of all the forces that are applied. It also includes the moments and the resultants. It is helpful to solve both simple and complex problems in mechanics.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Trending doubts
1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Draw a diagram of nephron and explain its structur class 11 biology CBSE

Explain zero factorial class 11 maths CBSE




