Ray Optics and Optical Instruments - An Important Concept for NEET
Let us first understand what optics is. Optics is a branch of physics that deals with the behaviour of light or other electromagnetic waves. Our eyes have the ability to detect electromagnetic waves in a certain range of wavelengths. Using this ability, we gain knowledge of the whole world.
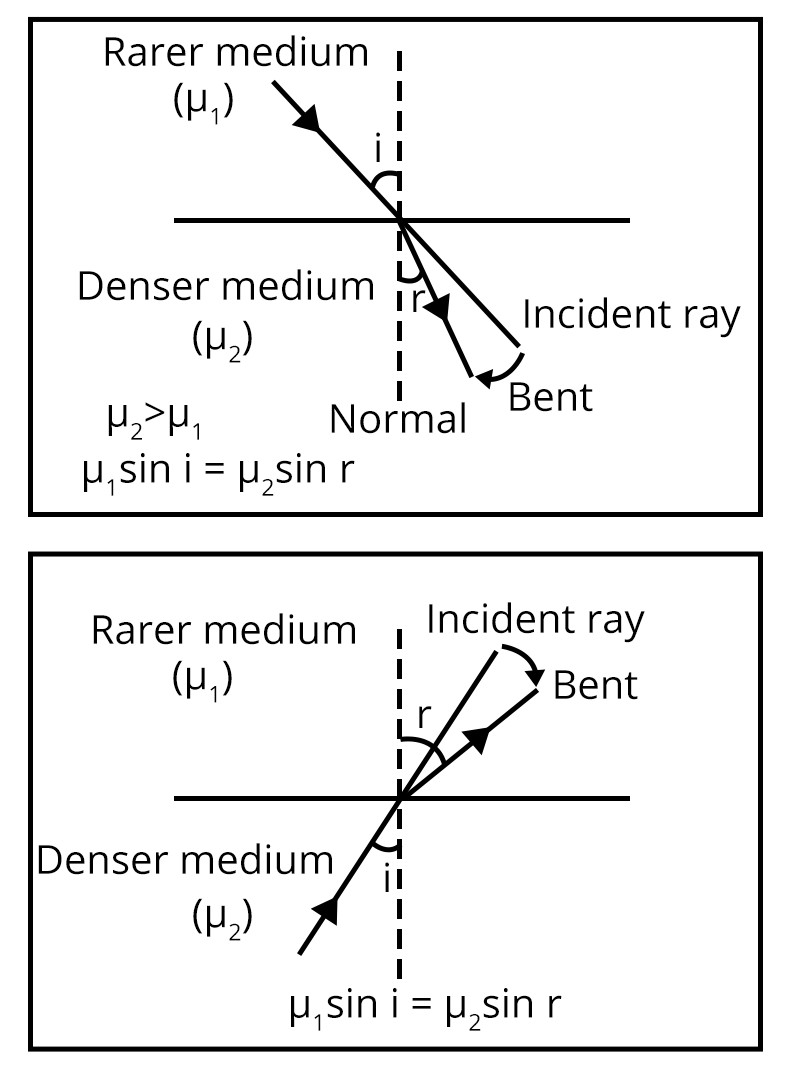
Light is a wave that travels in a straight light and doesn’t require a medium for its propagation. The path is called a ray of light and a bundle of such rays is called the beam of light.
In this chapter, students will learn about the behaviour of a beam of light when it encounters optical devices like mirrors and lenses. This part of optics is called geometric optics. Going further in this chapter, students will also learn about the construction and working of some important optical instruments and devices.
Now, let us move on to the important concepts and formulae related to the NEET exam along with a few solved examples.
Important Topics of Ray Optics and Optical Instruments
Reflection of Light
Mirror Formula
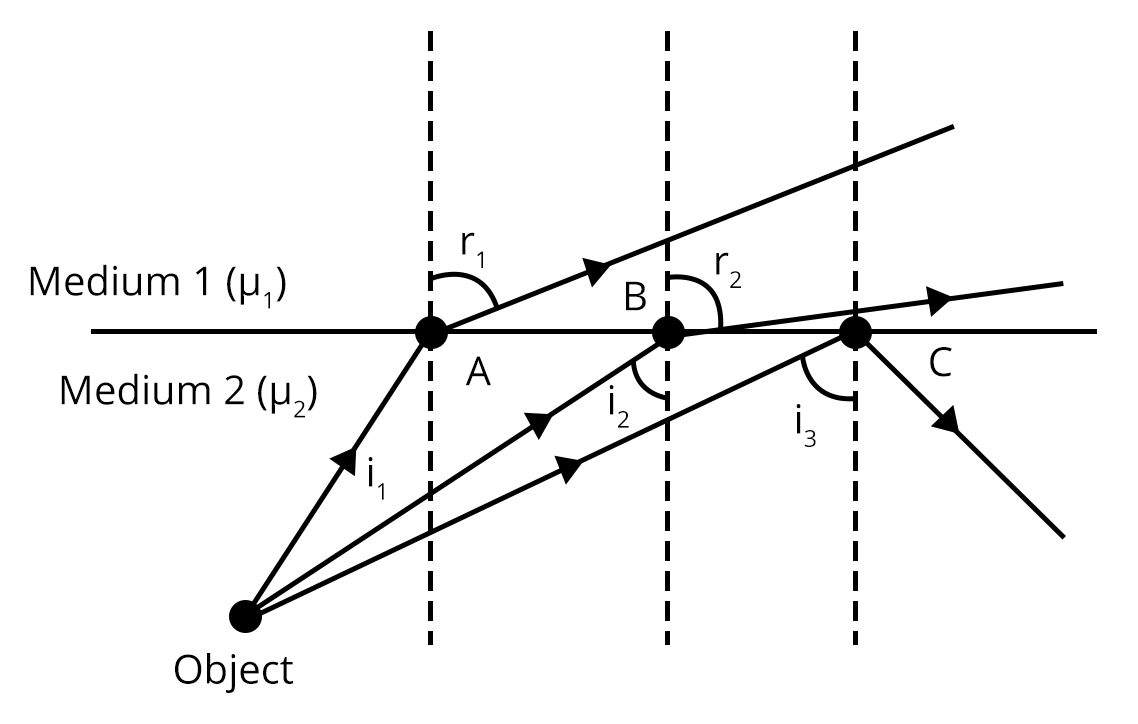
Refraction of Light
Lens
Total Internal Reflection
Deviation by a Prism
Dispersion by a Prism
Optical Instruments
Resolving Power of Optical Instruments
Important Concepts of Ray Optics and Optical Instruments
List of Important Formulae
Solved Examples
1. A thin rod of length $\dfrac{f}{3}$ is lying along a principal axis of the concave mirror of focal length f. The image is real, magnified and inverted and one of the ends of the rod coincides with its image itself. Find the length of the image.
Sol:
The given image is real, magnified and inverted. So, the object must lie between the focus and centre of curvature of the concave mirror. Now, it is also given that the image of one of the ends of the rods coincides on itself which means that one end will be at the centre of curvature. The position of the rod must look like the figure shown below.
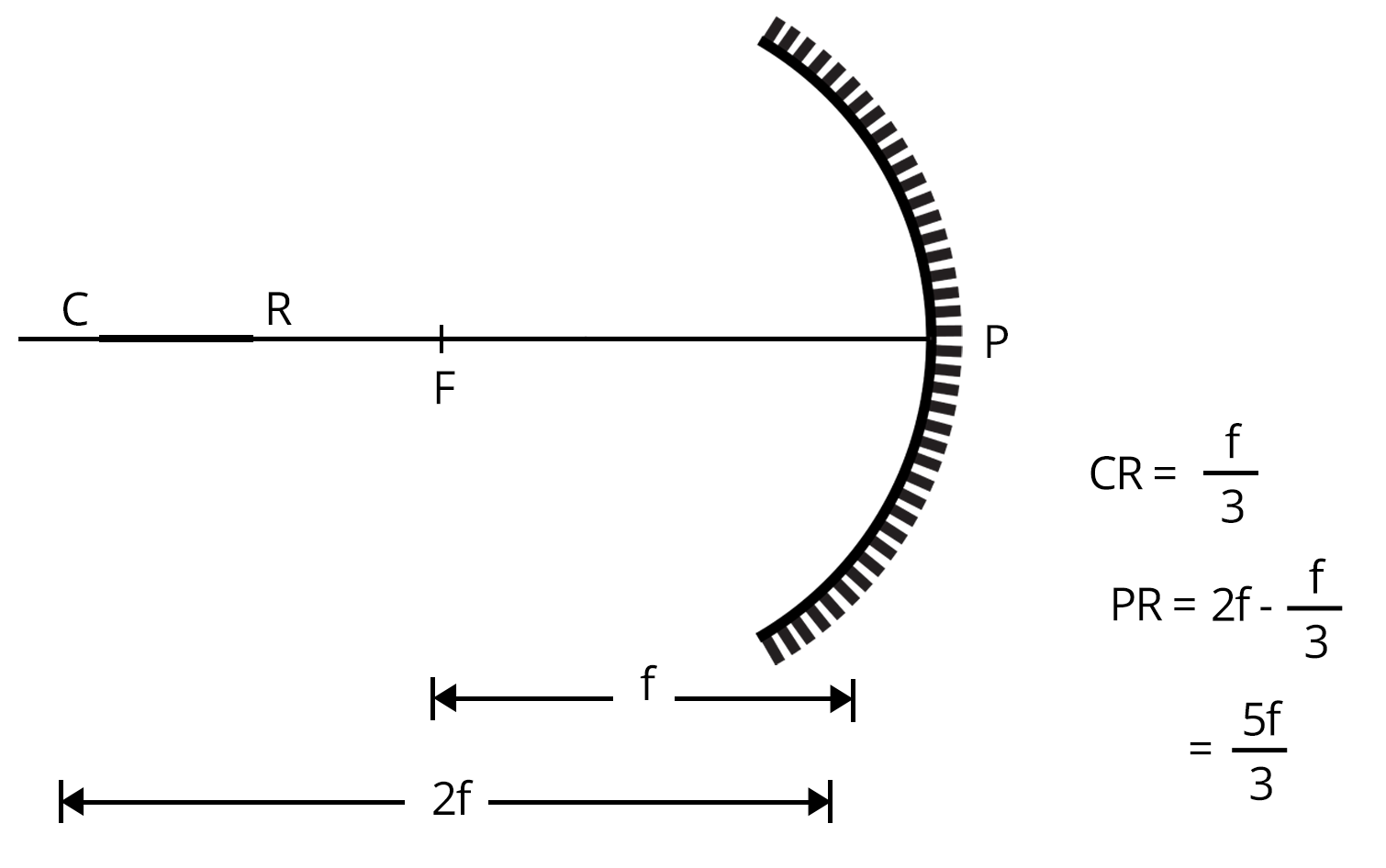
The image of end C coincides with the end C of the object. Now, let us find the image distance of point R. The distance of R from the pole of the concave mirror is PR i.e. $\dfrac{5f}{3}$.
Therefore, object distance (u) = $-\dfrac{5f}{3}$,
Using mirror formula:
$\dfrac{1}{f}= \dfrac{1}{v}+\dfrac{1}{u}$
$-\dfrac{1}{f}= \dfrac{1}{v}-\dfrac{3}{5f}$
Solving the equation, we get
$v= -\dfrac{5f}{2}$
So, let the image of CR be C’R’ then it would look like the figure shown below:
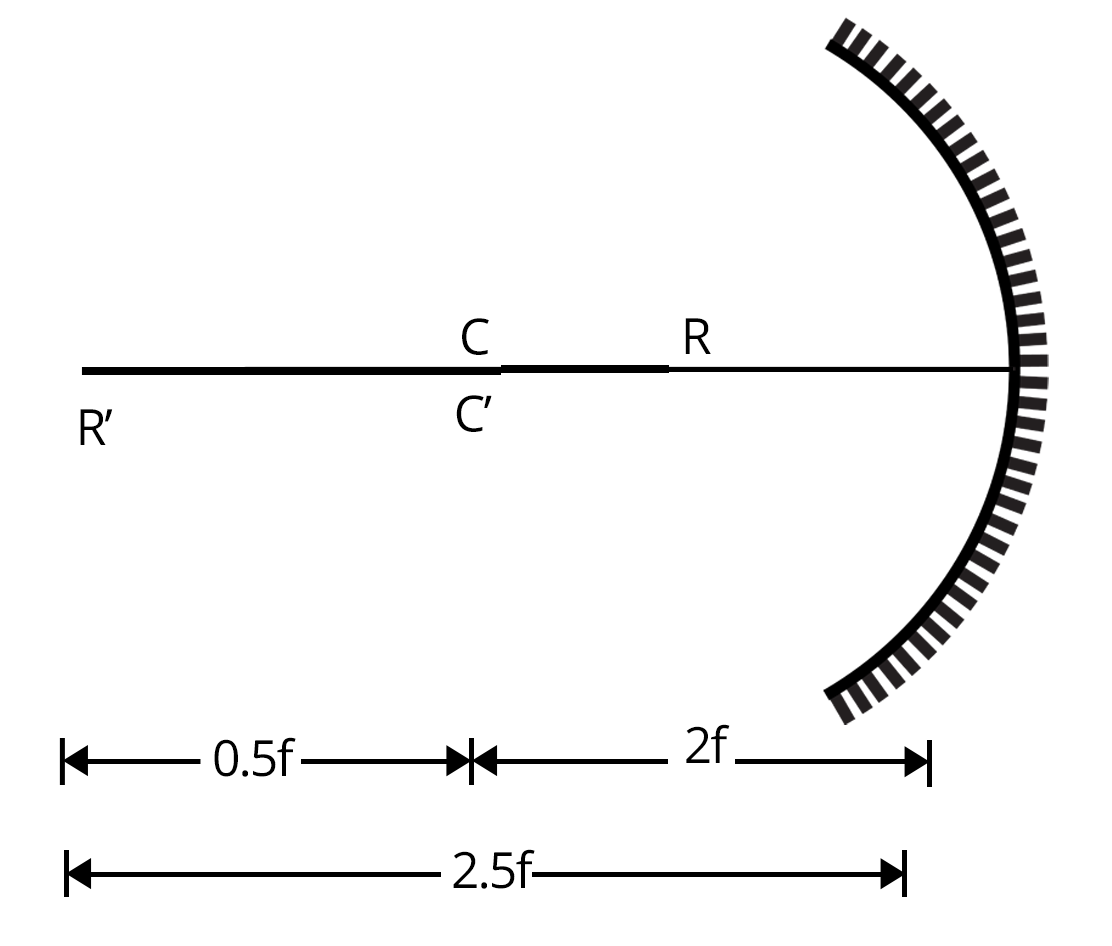
From the figure, length of rod, CR will be 0.5f
Key point: In such a case, the magnification is given by m = $- \dfrac{\text{length of image}}{\text{length of object}}$
2. The angle of minimum deviation for a glass prism with $\mu= \sqrt{3}$ equals the refractive angle of the prism. What is the angle of the prism?
Sol:
Let,
The angle of the prism be A.
The angle of minimum deviation be $\delta_m$.
In the question, it is given that angle of minimum deviation is equal to the refractive angle of the prism, then A = $\delta_m$
Using the formula for minimum deviation:
$\mu=\dfrac{\sin\lgroup\dfrac{\delta_m+A}{2}\rgroup}{\sin\lgroup\dfrac{A}{2}\rgroup}$
Also given that $\mu= \sqrt{3}$
Therefore,
$\sqrt{3}= \dfrac{\sin\lgroup\dfrac{A+A}{2}\rgroup}{\sin\lgroup\dfrac{A}{2}\rgroup}$
$\sqrt{3}= \dfrac{\sin A}{\sin\lgroup\dfrac{A}{2}\rgroup}$
$\sqrt{3}=\dfrac{2\sin\lgroup\dfrac{A}{2}\rgroup\cos\lgroup\dfrac{A}{2}\rgroup}{\sin\lgroup\dfrac{A}{2}\rgroup}$
$\cos\lgroup\dfrac{A}{2}\rgroup= \dfrac{\sqrt{3}}{2}$
A = 60°
Therefore, the angle of the prism will be 60°.
Key Point: Minimum deviation occurs when the angle of incidence on the one plane of the prism is equal to the angle of emergence on the other plane of the prism.
Previous Year Questions From NEET Paper
1. Find the value of the angle of emergence from the prism. The refractive index of the glass is $\sqrt{3}$ (NEET 2021)
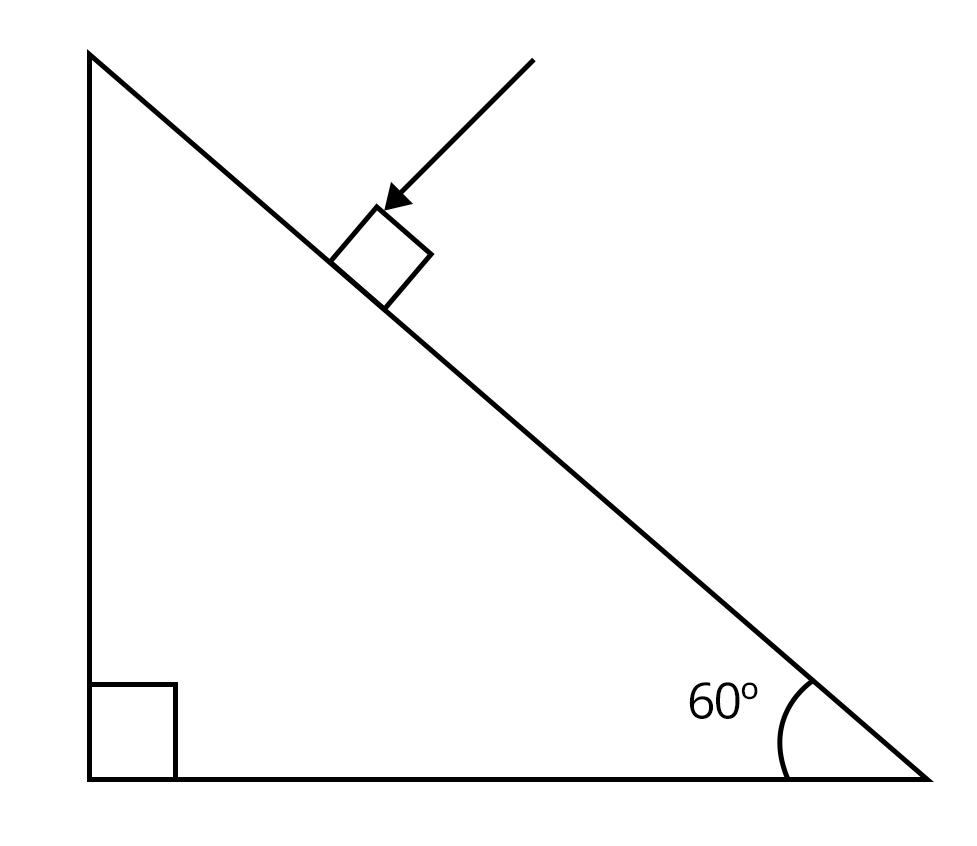
60°
45°
30°
90°
Sol:
Given, the refractive index $(\mu_1) = \sqrt{3}$
We know, refractive index of air $(\mu_2) = 1$
Now, from the figure given below:
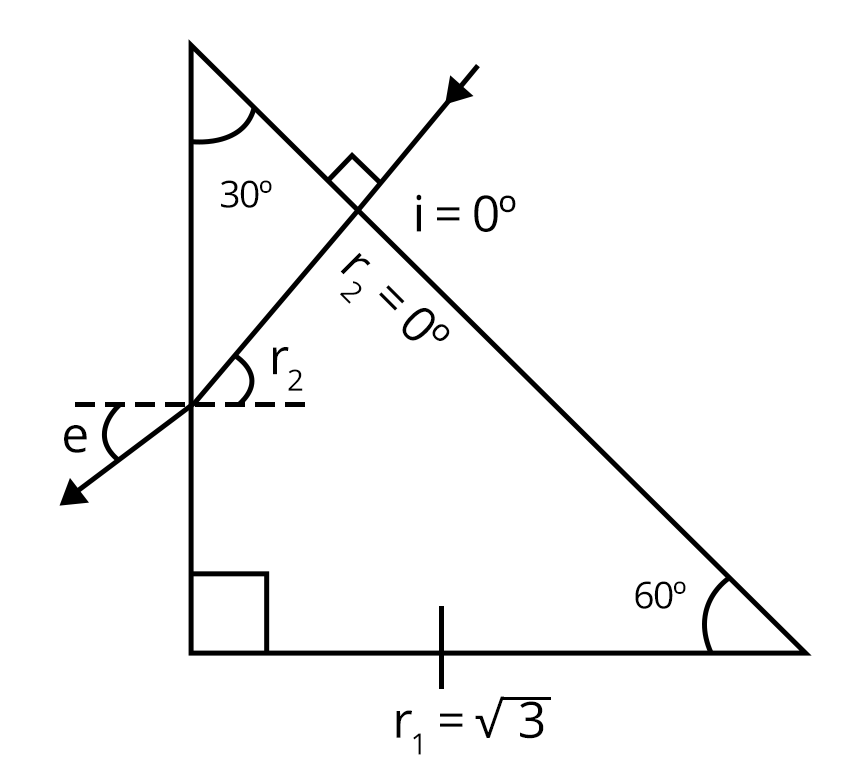
Angle of refraction from the first surface, $r_1$= 0°
Also, $A = r_1+r_2$
Where, A = angle of prism
Therefore, 30°=0°+$r_2$
Then, $r_2$ = 30°
Now, using Snell’s law:
$\mu_2\sin\theta_2= \mu_1\sin\theta_1$
$\sqrt{3}\sin30= 1\times\sin e$
$\sin e = \dfrac{\sqrt{3}}{2}$
e = 60°
Hence, the correct answer is option (a).
Trick: In these types of questions, always complete the ray diagram first. It will help in understanding the situation well.
2. A lens of large focal length and large aperture is best suited as an objective of an astronomical telescope since (NEET 2021)
a large aperture contributes to the quality and visibility of the images.
a large area of the objective ensures better light-gathering power.
a large aperture provides a better resolution
All of the above.
Sol:
Resolving power of optical instruments is given by RP = $\dfrac{1}{\text{d}\theta} = \dfrac{D}{1.22\lambda}$. Therefore, the greater the aperture, the greater will be the resolving power and hence better resolution, and quality of the image will be formed.
Option (d) is the correct answer.
Trick: We use astronomical telescopes for better quality and resolution.
Practice Questions
1. A ray of light is incident at an angle of 60° on the face of a prism having a refracting angle of 30°. The ray emerging out of the prism makes an angle of 30° with the incident ray. Show that the emergent ray is perpendicular to the face through which it emerges. (Ans. 0°)
2. A source of light is located at double focal length from a convergent lens. The focal length of the lens is f cm = 30. At what distance from the lens should a flat mirror be placed so that the rays reflected from the mirror are parallel after passing through the lens for the second time? (Ans. 45 cm)
Conclusion
In this article, we have provided important information regarding the chapter Ray Optics and Optical Instruments such as important concepts, formulae, etc. Students should work on more solved examples for securing good grades in the NEET2022 exam.
NEET Important Chapter - Ray Optics and Optical Instruments

 Share
ShareFAQs on NEET Important Chapter - Ray Optics and Optical Instruments
1. What is the weightage of the Ray Optics and Optical Instruments in NEET?
Nearly 3-4 questions arise in the exam from this chapter. Due to the weightage of the chapter, it is a must to practice this ch
2. What are the key points that need to be practised for solving questions from Ray Optics and Optical Instruments?
Students should concentrate on understanding the basics of reflection and refraction such as laws of refraction and reflection, rules for image formation in both reflection and refraction etc. and try solving different types of MCQ problems to grasp the concepts better. For NCERT, students should practice the derivations of important formulae.
3. Are previous year's questions enough for NEET?
To score 640+ in NEET, NCERT (both 11th and 12th) and previous year NEET Mains papers are sufficient. Solving previous 10-year NEET examinations offers us a tremendous advantage because 6-7 questions with identical alternatives are guaranteed to be repeated every year.




















 Watch Video
Watch Video