Class 9 Quadrilaterals Exercise 8.1 Solutions with Clear Step by Step Guidance
NCERT Solutions For Class 9 Maths Chapter 8 Quadrilaterals Exercise 8.1 (2025-26)
FAQs on NCERT Solutions For Class 9 Maths Chapter 8 Quadrilaterals Exercise 8.1 (2025-26)
1. What are NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals Exercise 8.1?
NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals Exercise 8.1 provide stepwise answers to questions based on properties and types of quadrilaterals. These solutions follow the CBSE 2025–26 guidelines and are structured to help students grasp core geometry concepts like parallelograms, rectangles, rhombuses, and squares.
2. How do NCERT Solutions for Chapter 8 Exercise 8.1 help in understanding the properties of parallelograms?
The solutions for Exercise 8.1 guide students through key properties of parallelograms such as equal opposite sides, equal opposite angles, and diagonals that bisect each other. Each step explains the reasoning in plain language, helping students learn how to apply these properties in problem-solving as per CBSE exam pattern.
3. Can practising all NCERT questions in Exercise 8.1 increase exam scores?
Yes. Consistently practising every NCERT question in Exercise 8.1 ensures students build confidence, spot common mistakes, and thoroughly internalize geometry concepts, which leads to improved marks in both school and CBSE board assessments.
4. Which theorems are introduced in Class 9 Maths Chapter 8 Exercise 8.1?
Important theorems in Class 9 Maths Chapter 8 Ex 8.1 include:
- Opposite sides of a parallelogram are equal
- Opposite angles of a parallelogram are equal
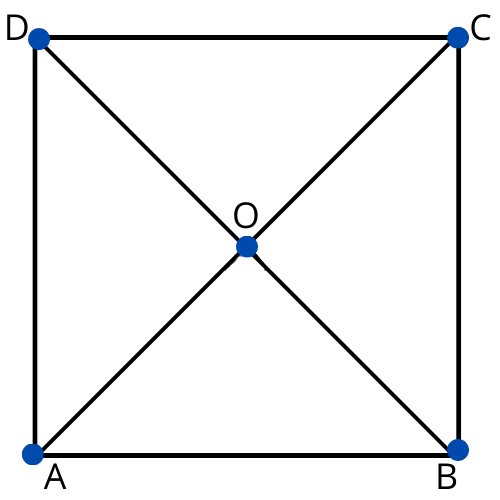
- The diagonals of a parallelogram bisect each other
5. What are the common types of quadrilaterals discussed in NCERT Solutions for Chapter 8 Exercise 8.1?
The main types of quadrilaterals covered are parallelograms, rectangles, squares, rhombuses, and trapeziums. The solutions clarify how to identify and differentiate them based on angles, sides, and diagonals.
6. How should CBSE students approach using the NCERT Solutions for Chapter 8 Exercise 8.1 effectively?
CBSE students should:
- Study stepwise logic for each answer
- Understand the reasoning, not just memorize steps
- Attempt questions before checking solutions for self-assessment
- Revise theorems and formulae regularly
7. Why is drawing diagrams important in Chapter 8 Exercise 8.1 solutions?
Accurate diagrams help visualize relationships between sides and angles in quadrilaterals, making it easier to apply properties correctly. CBSE examiners also value clean, labeled diagrams in geometry answers.
8. What is the angle sum property as explained in NCERT Solutions for Class 9 Chapter 8?
The angle sum property states that the sum of all interior angles of a quadrilateral is always 360°. This property is commonly used to solve for unknown angles within Exercise 8.1 questions.
9. How do NCERT Solutions for Quadrilaterals improve problem-solving skills?
Solutions explain logical steps to break down proofs, verify properties, and deduce new facts from given data. They train students in structured, exam-oriented mathematical reasoning.
10. What should students focus on in Chapter 8 Exercise 8.1 for board exam success?
Students should master identifying quadrilateral types, applying theorems, constructing proofs, and presenting clear diagrams and logic. Special emphasis on properties of parallelograms and problem-solving methodology is crucial for CBSE scoring.
11. Are the NCERT Solutions for Exercise 8.1 reliable for last-minute revision?
Yes, Vedantu's NCERT Solutions align with CBSE 2025–26 standards and offer concise, stepwise, and fully explained answers—ideal for fast revision and clearing common doubts before exams.
12. What are some common misconceptions students have about parallelograms in Chapter 8?
Common misconceptions:
- Assuming all parallelograms are rectangles or squares
- Believing diagonals are always equal (only true for rectangles and squares)
- Confusing properties between rhombus and rectangle
13. How can students avoid mistakes in proving properties of quadrilaterals?
Carefully apply each step as per theorem requirements, label diagrams clearly, and check if all properties used are valid for the given quadrilateral type. NCERT Solutions model this approach for every question in Exercise 8.1.
14. What should students do if they struggle with proofs in Quadrilaterals Chapter 8?
Start by revisiting basic definitions, practice similar solved examples, and break proofs into clear, logical steps. Using NCERT Solutions alongside classroom notes builds confidence and accuracy in geometry proofs.
15. How are the side and angle relationships of parallelograms illustrated in Exercise 8.1 of Class 9 Maths?
Exercise 8.1 provides step-wise explanations, often using congruency of triangles to show why opposite sides and angles are equal, and how diagonals bisect each other, supported by labeled geometrical diagrams.














 Watch Video
Watch Video