Class 9 Maths Exercise 11.2 – Surface Areas and Volumes Solutions
NCERT Solutions for Class 9 Maths Chapter 11 Exercise 11.2 Surface Areas and Volumes
FAQs on NCERT Solutions for Class 9 Maths Chapter 11 Exercise 11.2 Surface Areas and Volumes
1. What are the main types of surface areas you learn about in NCERT Solutions for Class 9 Maths Chapter 11 Surface Areas and Volumes Exercise 11.2?
In Chapter 11 Exercise 11.2, you study curved surface area, lateral surface area, and total surface area for 3D shapes such as cylinders, cones, spheres, cuboids, and cubes, following the official CBSE 2025–26 syllabus.
2. How do you approach solving a Class 9 Maths surface area problem using NCERT solutions methodology?
To solve a surface area problem using NCERT solutions:
- Identify the 3D shape and required surface area type
- Write down the relevant formula from the CBSE syllabus
- Substitute the given measurements (e.g., radius, height, length)
- Calculate and express the answer in correct units (cm2 or m2)
3. Why is the formula for the surface area of a sphere always $4\pi r^2$ in NCERT Class 9 Chapter 11?
The formula $4\pi r^2$ covers the total surface encapsulating a sphere, as a sphere is perfectly symmetrical in all directions. This ensures all points on the surface are at an equal distance (radius r) from the center, which is central to Chapter 11's CBSE-conceptual focus.
4. What is the difference between the volume and surface area of a 3D shape as per NCERT Solutions Class 9 Maths Chapter 11?
Surface area measures the total area covering the exterior of a solid, while volume represents the space or capacity inside the shape. For example, a cylinder’s surface area finds the outside area, whereas its volume gives the amount it can hold, both as per Class 9 NCERT Maths guidelines.
5. How do you calculate the total surface area of a hemisphere in NCERT Class 9 Maths Chapter 11?
For a hemisphere:
- Curved surface area = $2\pi r^2$
- Total surface area = $2\pi r^2 + \pi r^2 = 3\pi r^2$
- Always use the value of π specified in the NCERT problem (commonly $\frac{22}{7}$ or 3.14).
6. In NCERT Solutions for Class 9 Maths Chapter 11 Surface Areas and Volumes, how do you handle questions involving both inner and outer surfaces, like a hollow sphere or bowl?
First, calculate inner and outer radii by adjusting for thickness. Then, use the appropriate surface area formula for each layer. For curved surface area of a hemisphere (e.g., a bowl), use $2\pi r^2$ with the correct radius for each layer, as modelled in Stepwise NCERT solutions.
7. FUQ: What are common mistakes students make when applying surface area and volume formulas in NCERT Class 9 Maths Chapter 11, and how to avoid them?
Common errors include:
- Using radius instead of diameter or vice versa (always check what’s given)
- Misapplying π (incorrect value, use the one suggested in the question)
- Mixing up formulas for different shapes
- Forgetting to convert units (e.g., cm to m)
8. FUQ: How can understanding surface areas and volumes as per NCERT Class 9 Maths help in real life?
These concepts are practical in daily life:
- Calculating paint required for a surface (surface area)
- Estimating water/storage capacity (volume)
- Designing containers, packaging, and construction
9. How does NCERT Solutions for Class 9 Maths Chapter 11 Exercise 11.2 ensure students follow CBSE marking guidelines?
Solutions are stepwise:
- State the correct formula and label all steps
- Show substitution and calculation
- Write the final answer with units
10. FUQ: If the radius of a sphere doubles, how does the surface area change according to Class 9 Maths Chapter 11?
Since surface area of a sphere is $4\pi r^2$, doubling the radius (2r) changes the area to $4\pi (2r)^2 = 16\pi r^2$, so surface area increases four times. This scaling concept is a key learning in Chapter 11 and often appears in higher-order questions.
11. What is the curved surface area of a right circular cylinder as per NCERT Class 9 Maths Chapter 11?
The curved surface area of a right circular cylinder is calculated as $2\pi rh$, where r is the radius and h is the height. This formula is applied exactly as shown in NCERT solutions Stepwise method.
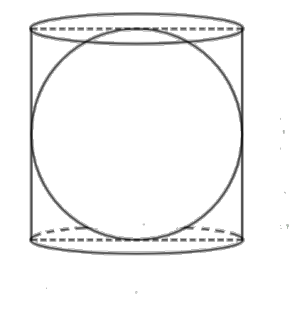
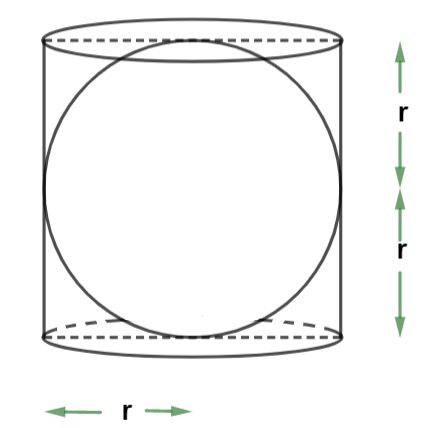
12. FUQ: Why does the curved surface area of a cylinder enclose the same area as a sphere of the same radius, as seen in one of the NCERT Exercise 11.2 problems?
If a right circular cylinder encloses a sphere perfectly (height = 2r), their curved surface areas become equal ($2\pi r * 2r = 4\pi r^2$), demonstrating a conceptual overlap explored in Chapter 11. This relationship deepens geometric understanding.
13. How should students show their work for full marks when writing NCERT solutions for Class 9 Maths Chapter 11 Exercise 11.2?
Write the question clearly, cite the correct formula, substitute values, show each calculation step, state the answer with units, and ensure clarity. This mirrors the marking scheme and presentation expected by CBSE examiners per the 2025–26 guidelines.
14. FUQ: In NCERT Class 9 Maths Chapter 11, what if two objects have the same volume but different surface areas—how does that affect real-world usage?
Objects with the same volume but different surface areas may differ in material cost, heat loss, or strength. For example, containers might hold equal amounts but need more/less covering material, an idea that shows the practical significance of these calculations.
15. FUQ: Why is practicing all the sums in Exercise 11.2 critical for CBSE exam prep in Class 9 Maths?
Each sum in Exercise 11.2 covers a unique scenario or formula application. Thorough practice exposes you to all likely CBSE patterns, avoids conceptual gaps, and improves confidence and speed for the actual exam.




















 Watch Video
Watch Video