Class 8 Maths Chapter 3 Questions and Answers - Free PDF Download
Class 8 Maths NCERT Solutions for Chapter 3 Exercise 3.4: Understanding Quadrilaterals provides detailed explanations for all questions in the exercise. Vedantu's subject experts created these solutions to help students successfully understand the various kinds of quadrilaterals. The main focus is on identifying the features and characteristics of different quadrilaterals, including parallelograms, trapeziums, and triangles.
Table of Content
This Exercise 3.4 Class 8 is important because it provides the basis for more complex geometric concepts. By studying these solutions, students can clear up their doubts and improve their knowledge of quadrilaterals. Vedantu provides clear and detailed solutions CBSE Class 8 Maths Syllabus to help students understand these concepts easily.
Exercise 3.4
1. State whether True or False.
(a) All rectangles are squares.
Ans: This statement is false.
Because all squares are rectangles but all rectangles are not square.
As in square, all sides are equal.
But in rectangles opposite sides are equal.
(b) All rhombuses are parallelograms.
Ans: This statement is true.
Because opposite sides are equal and opposite sides are parallel in a rhombus.
(c) All squares are rhombuses and also rectangles.
Ans: This statement is true.
Because in rhombuses opposite sides are equal and parallel, so as in square.
In a rectangle opposite sides are equal and parallel, so as in square.
(d) All squares are not parallelograms.
Ans: This statement is false.
All squares are parallelograms.
Because in a square all sides are equal and opposite sides are parallel.
(e) All kites are rhombuses.
Ans: This statement is false.
Because in kites opposite sides are not equal. The Diagonal top of the kite is not equal.
(f) All rhombuses are kites.
Ans:This statement is true.
As rhombuses also have two consecutive sides they are equal as in kite.
(g) All parallelograms are trapeziums.
Ans: This statement is true.
Because all parallelograms have pairs of parallel sides.
(h) All squares are trapeziums.
Ans: This statement is true.
Because all squares have a pair of parallel sides.
2. Identify all the quadrilaterals that have
(a) four sides of equal length
Ans: Square and rhombuses are the quadrilaterals which have all four sides of equal length.
(b) four right angles
Ans: Square and rectangle are the quadrilaterals which have all four angles.
3. Explain how a square is.
(i) a quadrilateral
Ans: A square is quadrilateral because it has four sides.
(ii) a parallelogram
Ans: A square is parallelogram because it’s opposite sides are of equal length and parallel. And opposite angles of the square are also equal.
(iii) a rhombus
Ans: A square rhombus is a square because the square has all sides of equal length.
(iv) a rectangle
Ans: A square is a rectangle because opposite sides are of equal length and all angles are right angles.
4. Name the quadrilaterals whose diagonals.
(i) bisect each other
Ans: Square, rectangle, rhombus and parallelogram are the quadrilaterals in which diagonals bisect each other.
(ii) are perpendicular bisectors of each other
Ans: Square and rhombus are the quadrilaterals in which diagonals are perpendicular bisectors of each other.
(iii) are equal
Ans: Rectangle, square and parallelogram are the quadrilaterals in which diagonals are equal.
5. Explain why a rectangle is a convex quadrilateral.
Ans: Rectangle is a convex quadrilateral because both diagonals of the rectangle are lying inside of the rectangle.
6. ABC is a right-angled triangle and O is the midpoint of the side opposite to the right angle. Explain why O is equidistant from A, B and C. (The dotted lines are drawn additionally to help you).
Ans:
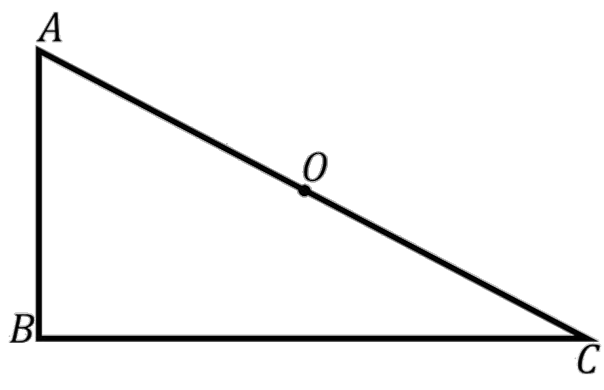
Given :\[ABC\] is a right angle triangle in which \[\angle B\] is right angle and \[O\] is a mid-point of \[AC\] .
Construction : Draw line \[AD{\text{ and }}DC\]such that \[AD\parallel BC\]and \[AB\parallel DC\] .
And, \[AB = DC,{\text{ }}AD = BC\]
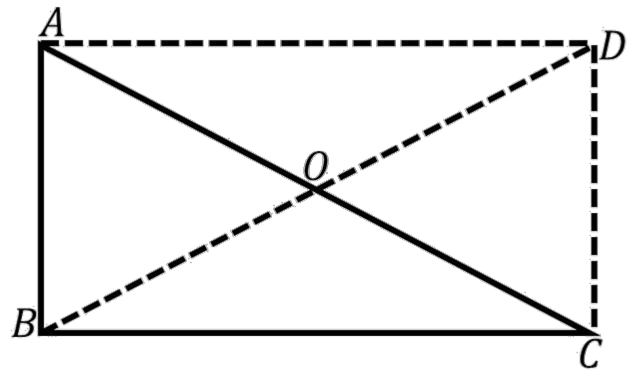
As, opposite sides are of equal length, opposite sides are parallel and also all interior angles are measure of \[90^\circ \].
Therefore, \[ABCD\] is a rectangle.
So, in a rectangle, diagonals of equal length bisect each other.
Therefore,
\[AO = OC = BO = OD\]
Hence, \[O\] is equidistant from \[A,B{\text{ and }}C\].
Conclusion
NCERT Solutions for Maths Ex 3.4 Class 8 Chapter 3 - Understanding Quadrilaterals provides simple solutions. Focus on understanding the characteristics of shapes such as squares, rectangles, parallelograms, rhombuses, and trapezoids. Understanding these features is necessary for solving problems correctly. Practising these tasks will help you develop a strong understanding of the subject and improve your geometry skills. These solutions make it easy to remember quadrilaterals and help you score well on exams.
Class 8 Maths Chapter 3: Exercises Breakdown
CBSE Class 8 Maths Chapter 3 Other Study Materials
Chapter-Specific NCERT Solutions for Class 8 Maths
Given below are the chapter-wise NCERT Solutions for Class 8 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.
Important Related Links for CBSE Class 8 Maths
