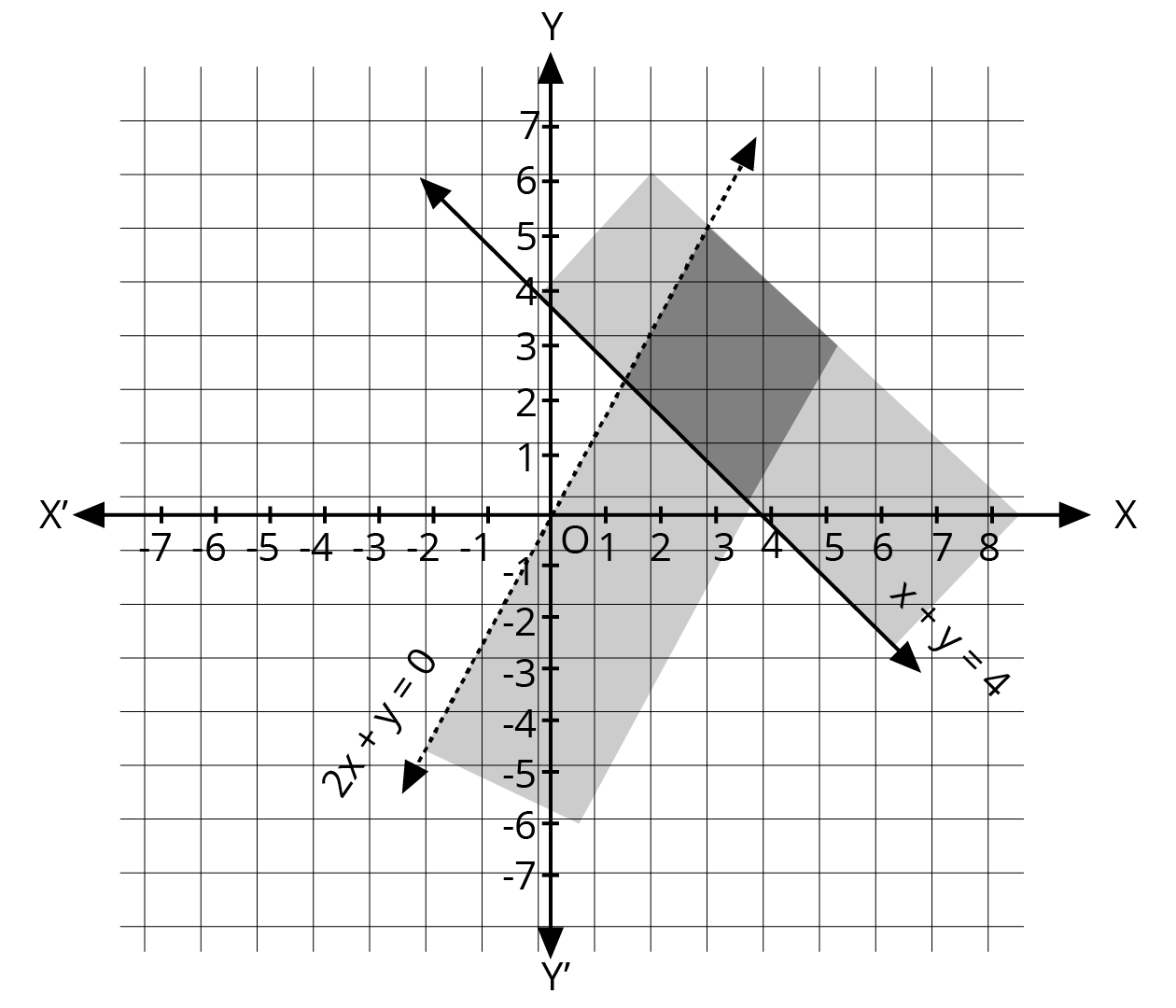Solved NCERT Questions For Class 11 Maths Chapter 6 In Hindi - Free PDF
FAQs on NCERT Solutions For Class 11 Maths Chapter 6 Linear Inequalities in Hindi - 2025-26
1. Where can I find reliable and step-by-step NCERT Solutions for Class 11 Maths Chapter 6, Linear Inequalities?
You can find comprehensive and accurate NCERT Solutions for Class 11 Maths Chapter 6, Linear Inequalities, right here on Vedantu. Our solutions are crafted by subject matter experts to provide a detailed, step-by-step methodology for every problem in the textbook. They are fully updated according to the latest CBSE 2025-26 syllabus and are designed to help you understand the correct approach to solving each question.
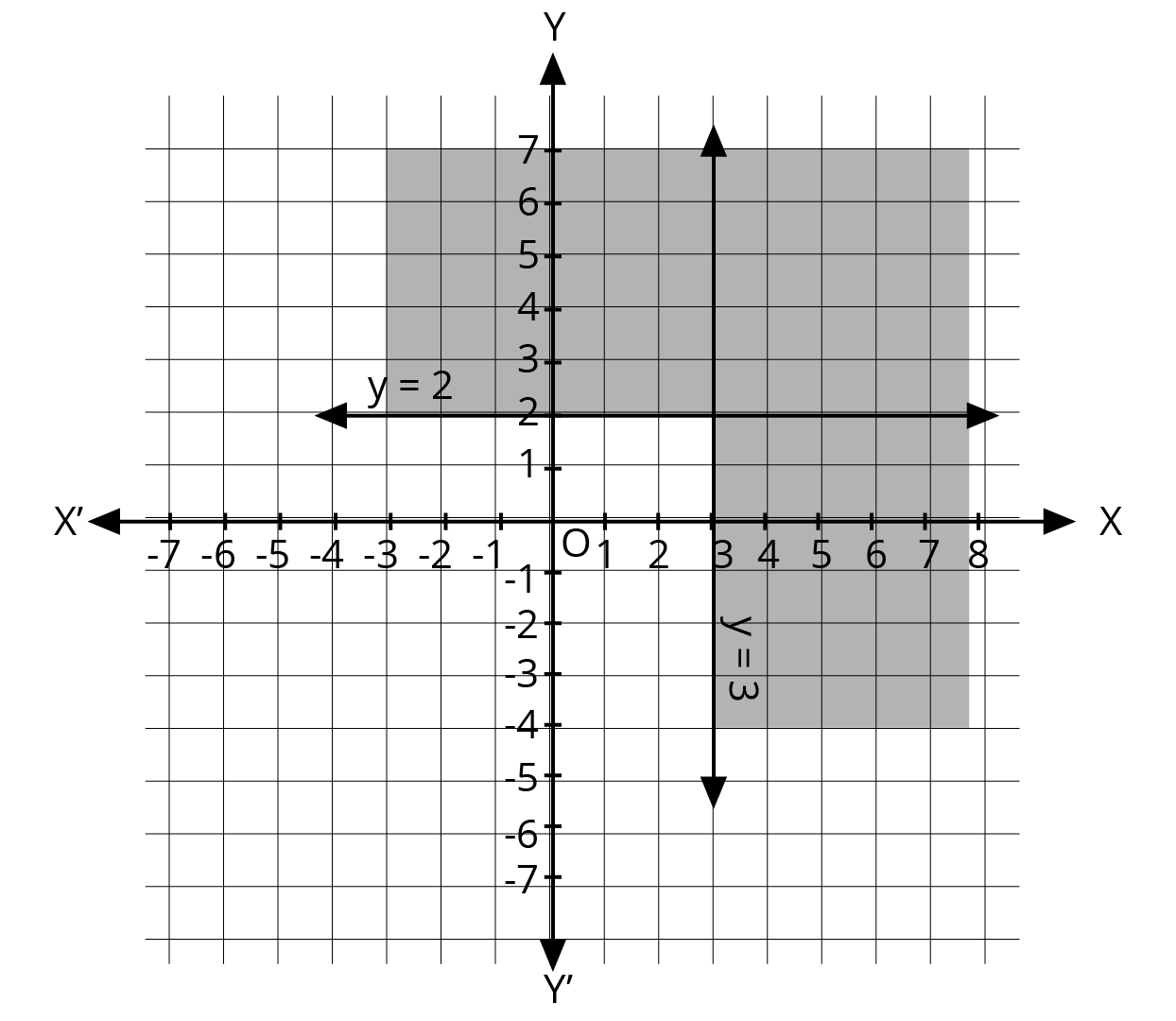
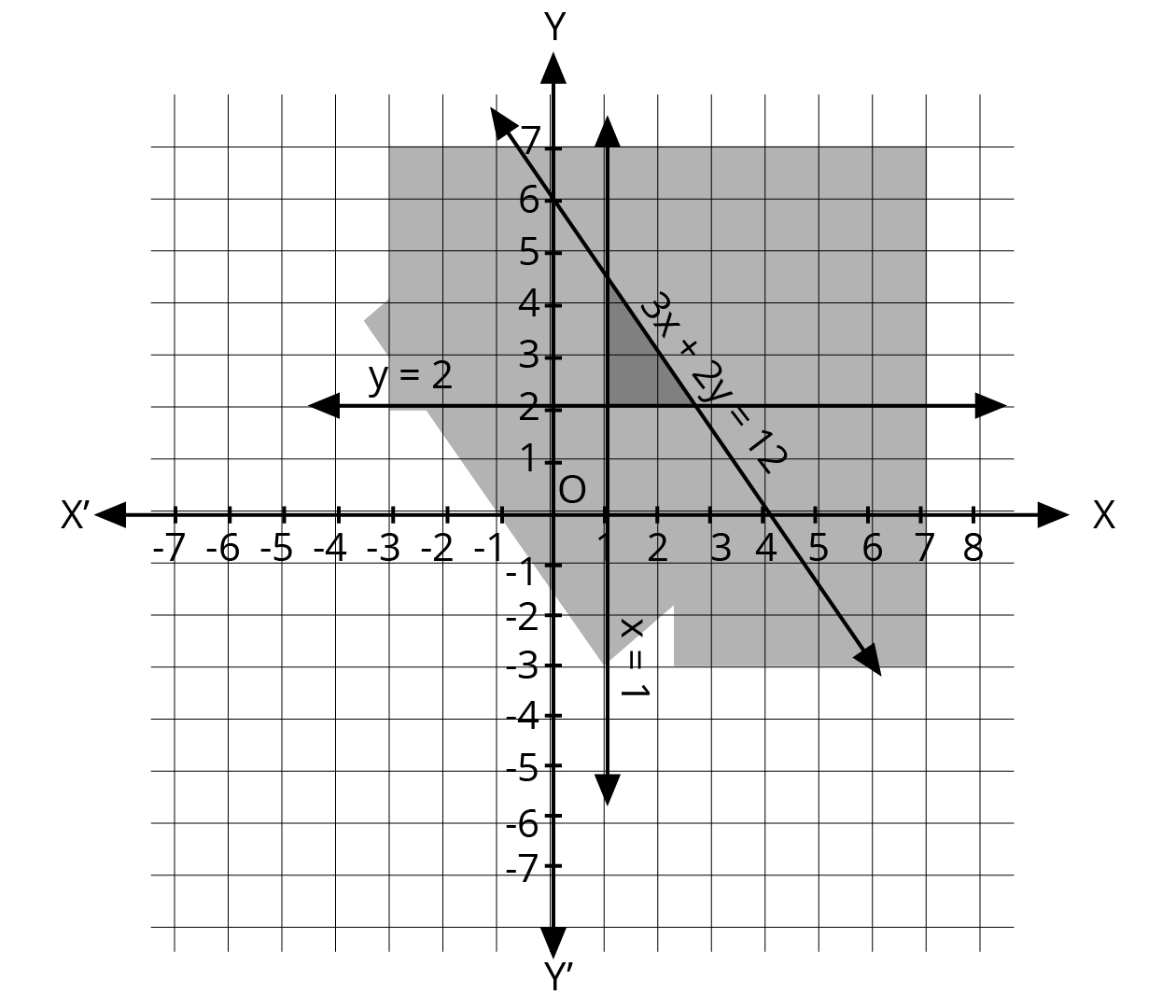
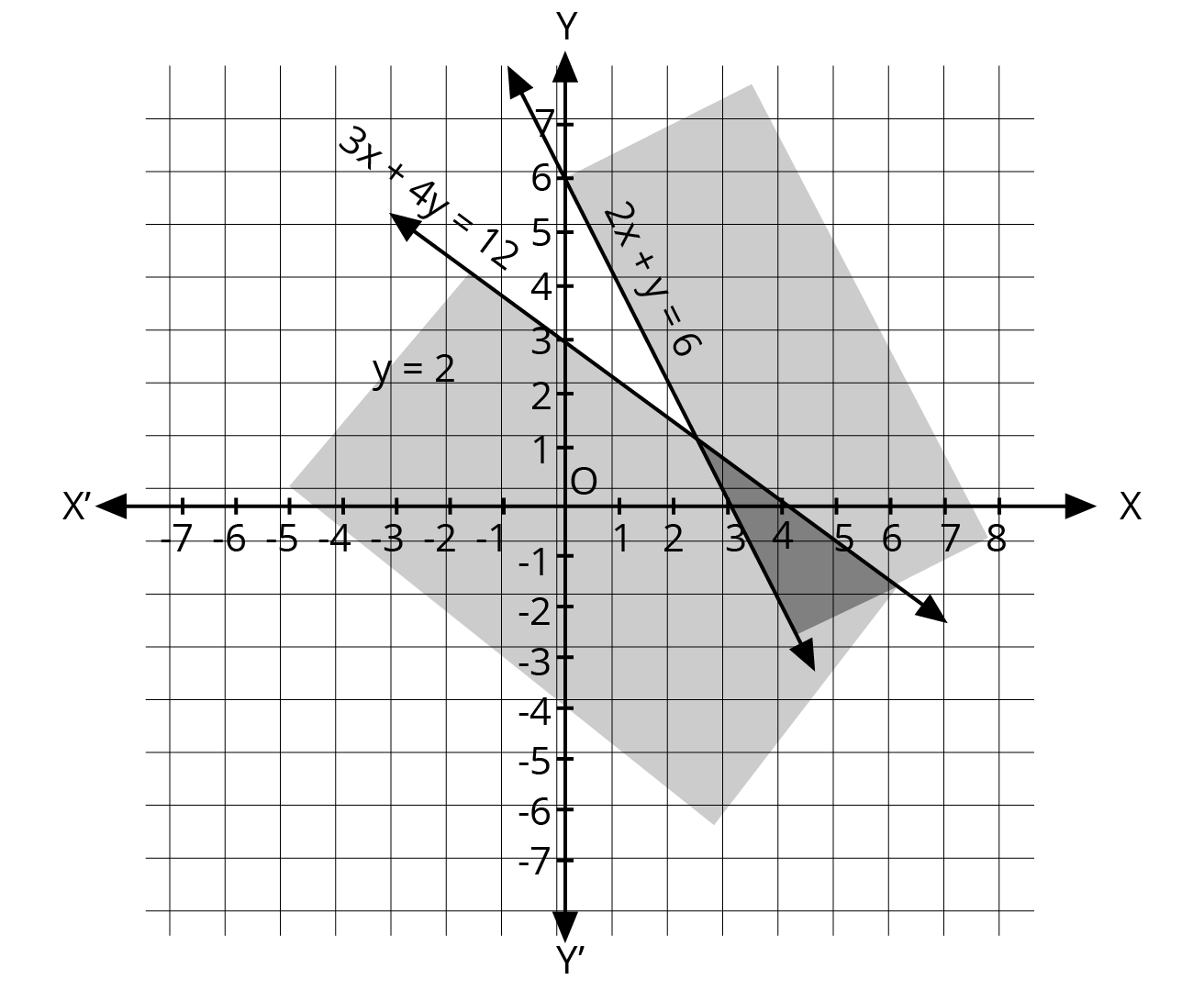
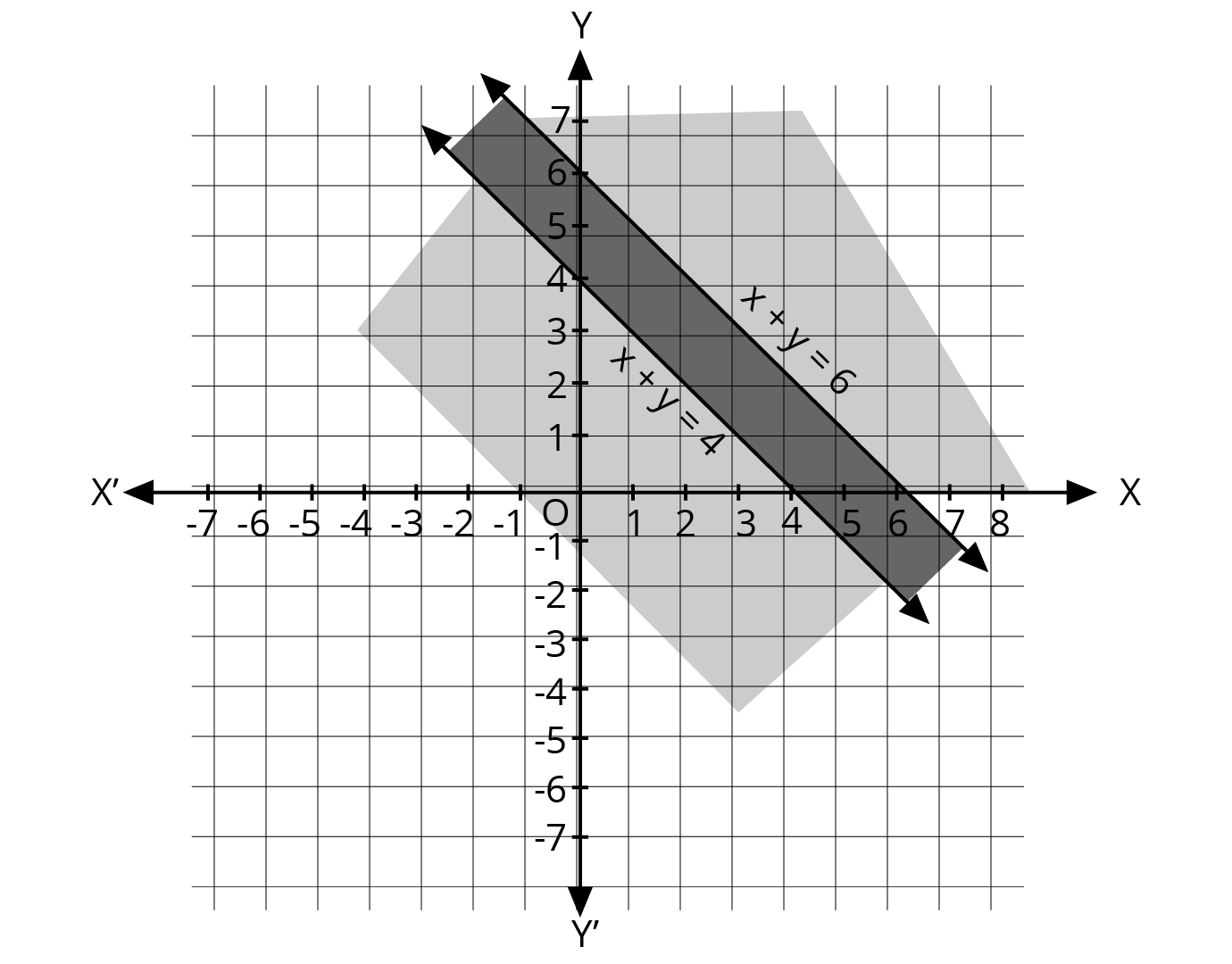
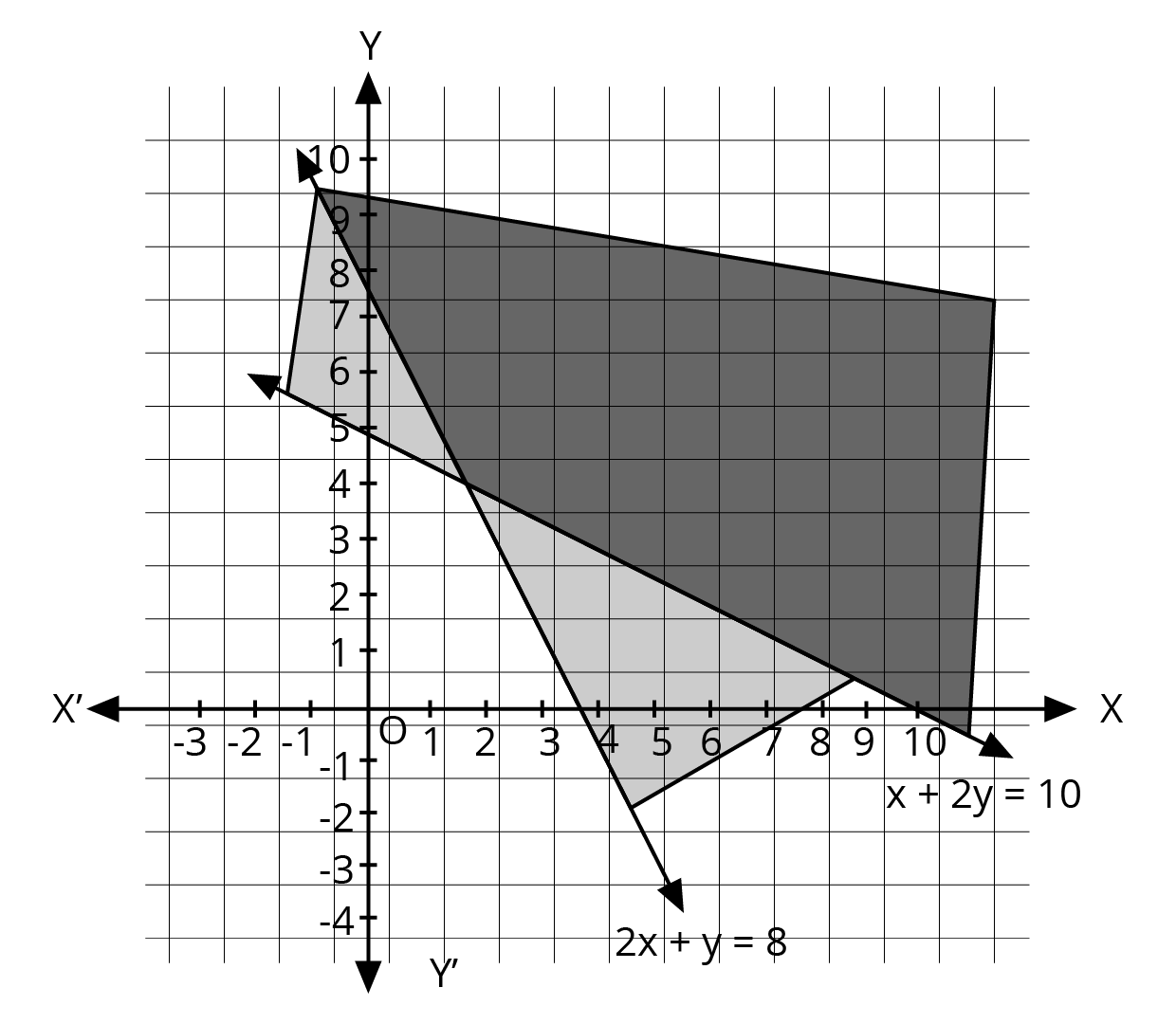
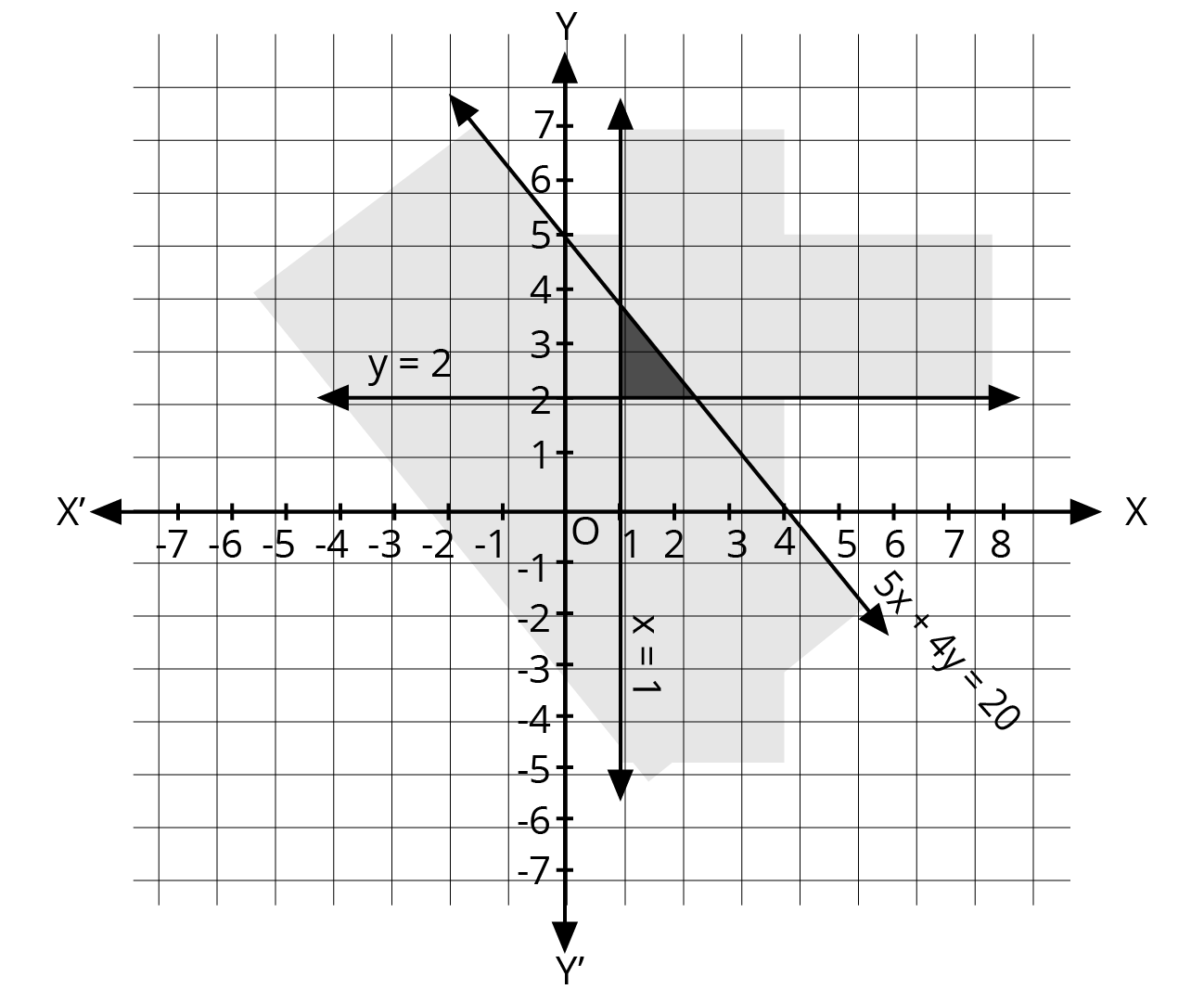
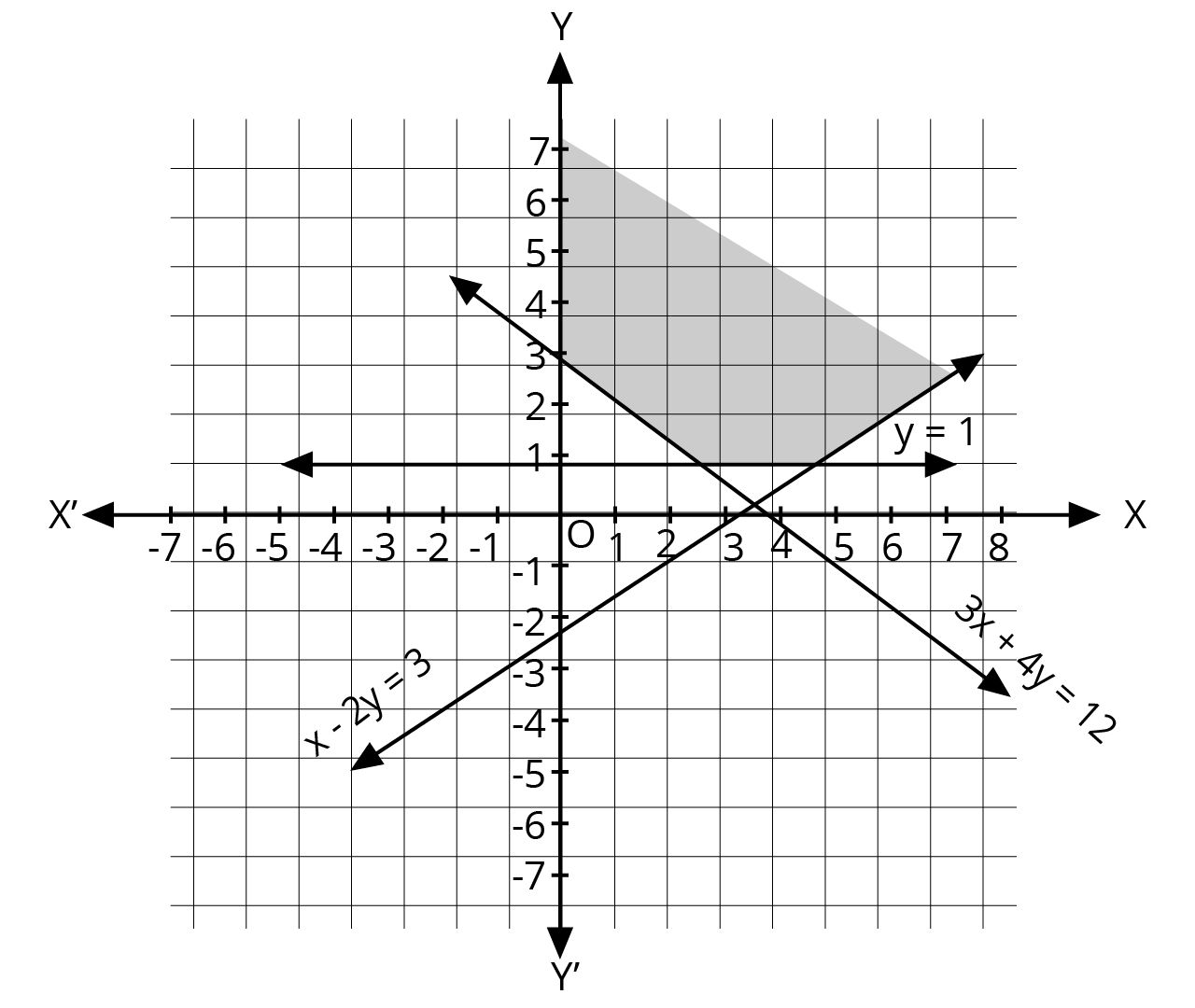
2. What is the correct method to solve a system of linear inequalities in two variables graphically, as per the NCERT solutions?
The NCERT-prescribed method for graphically solving a system of linear inequalities involves a clear, step-by-step process:
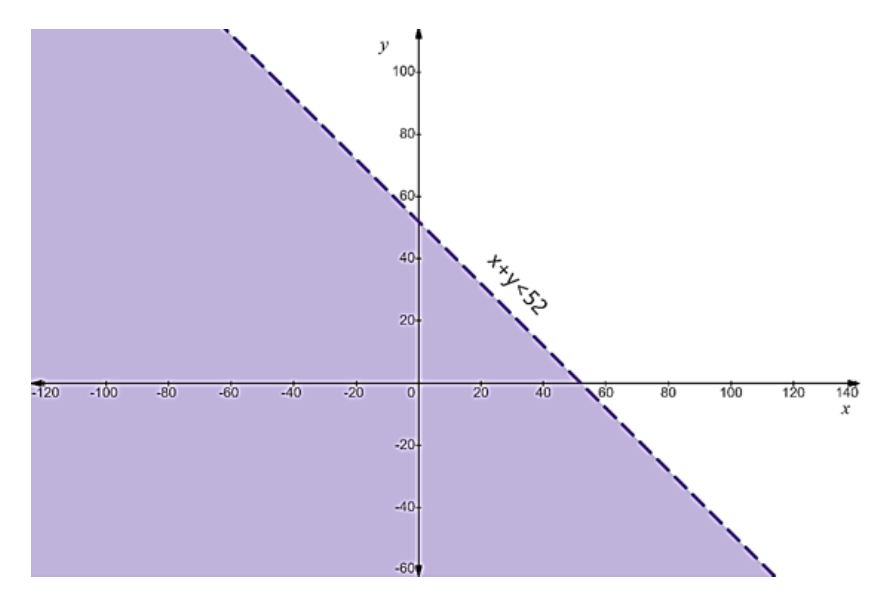
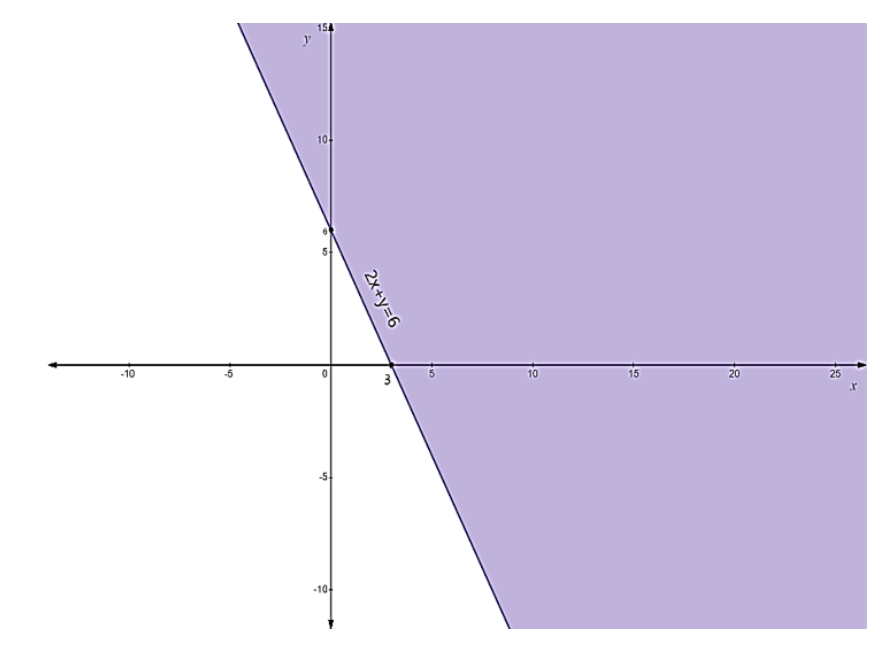
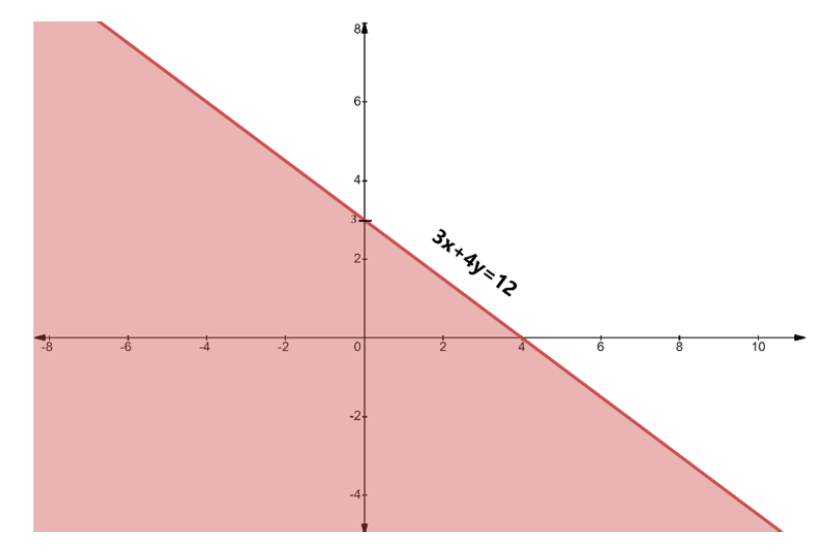
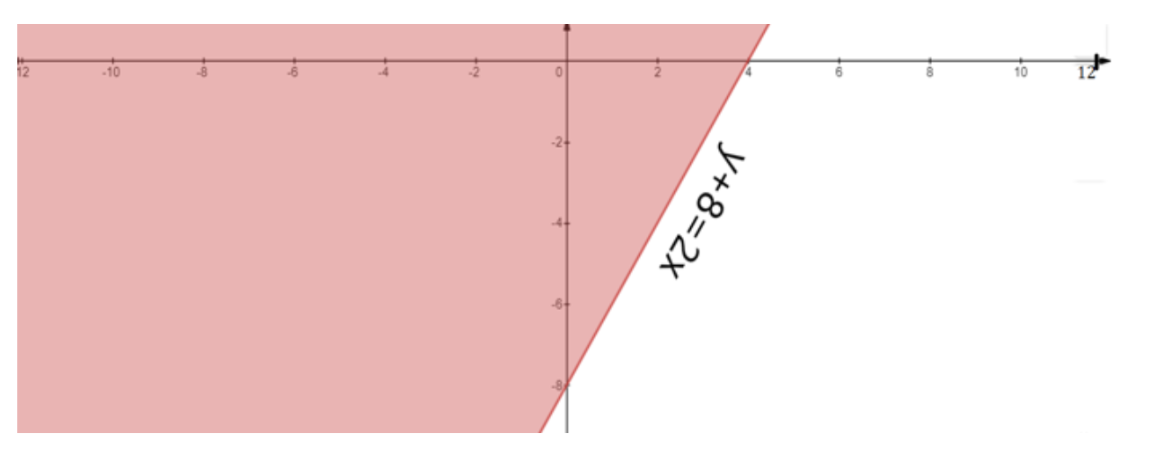
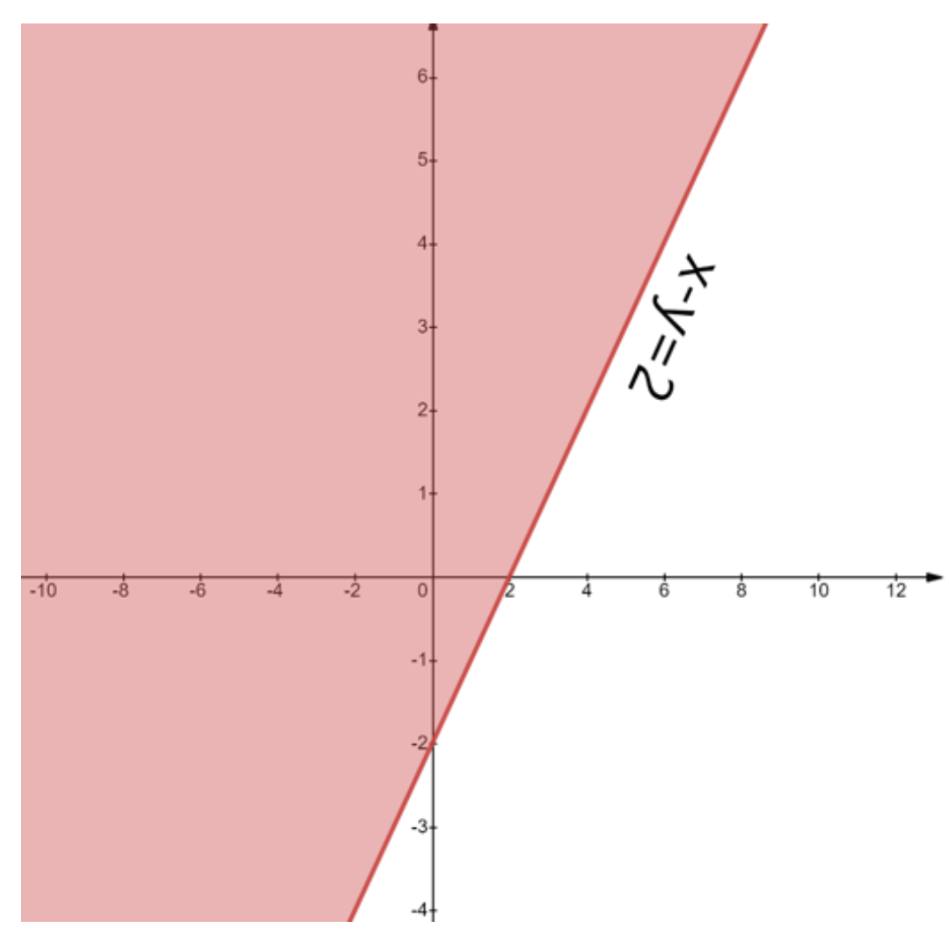
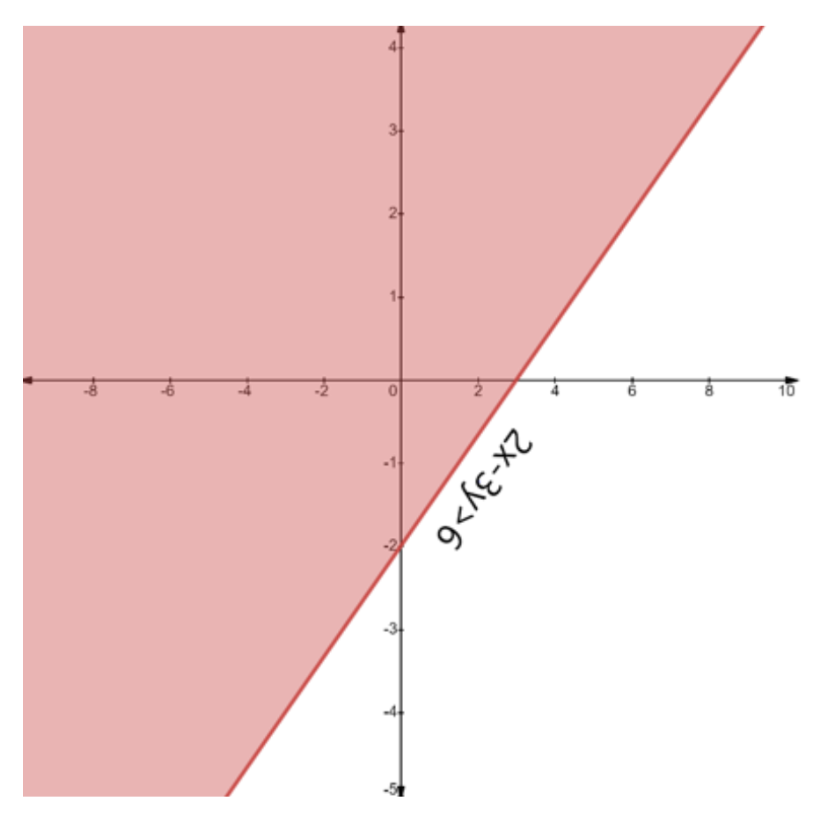
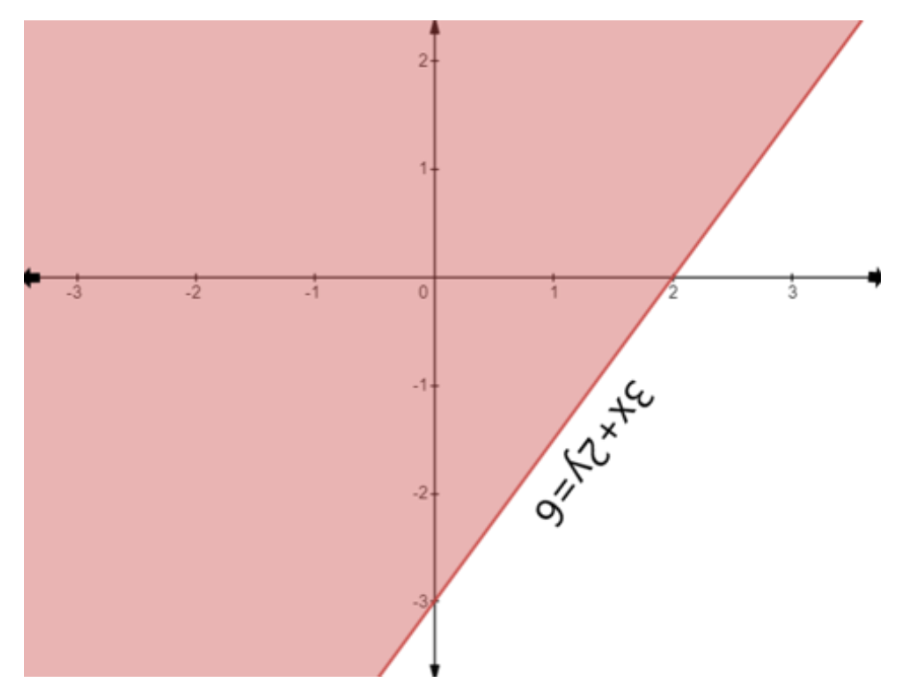
- First, treat each inequality as an equation (e.g., replace ≤ with =) to plot the boundary line on a graph.
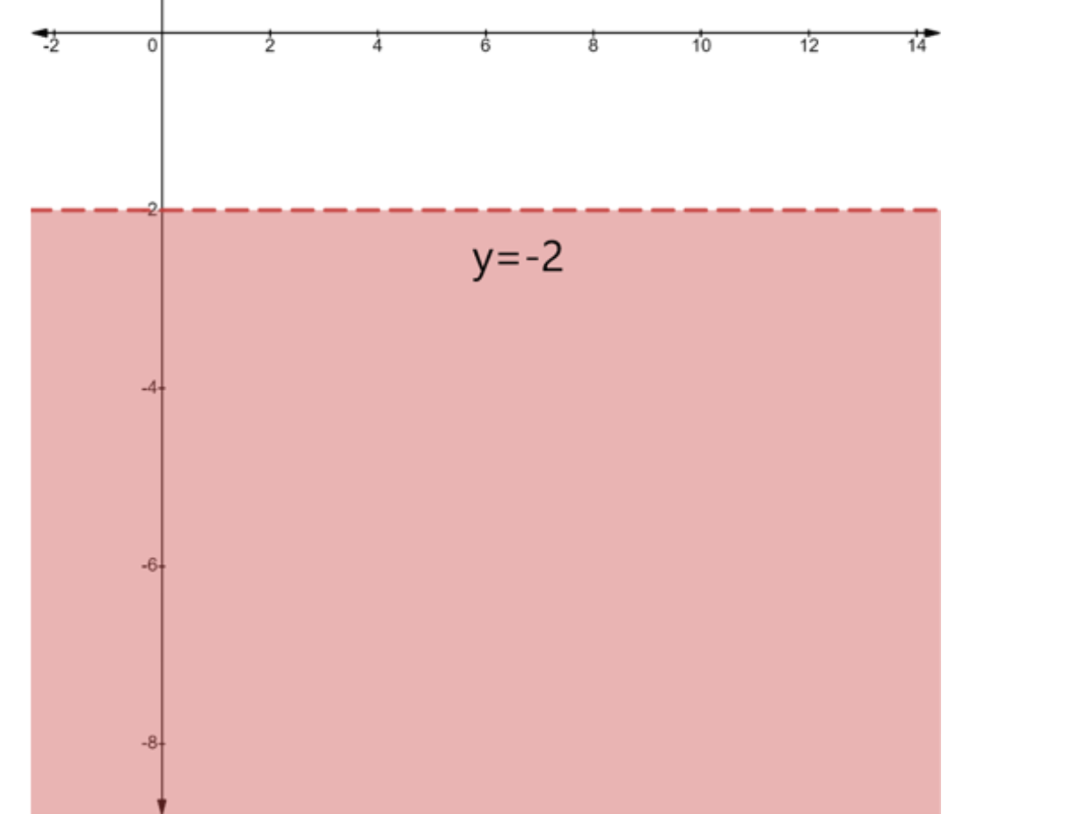
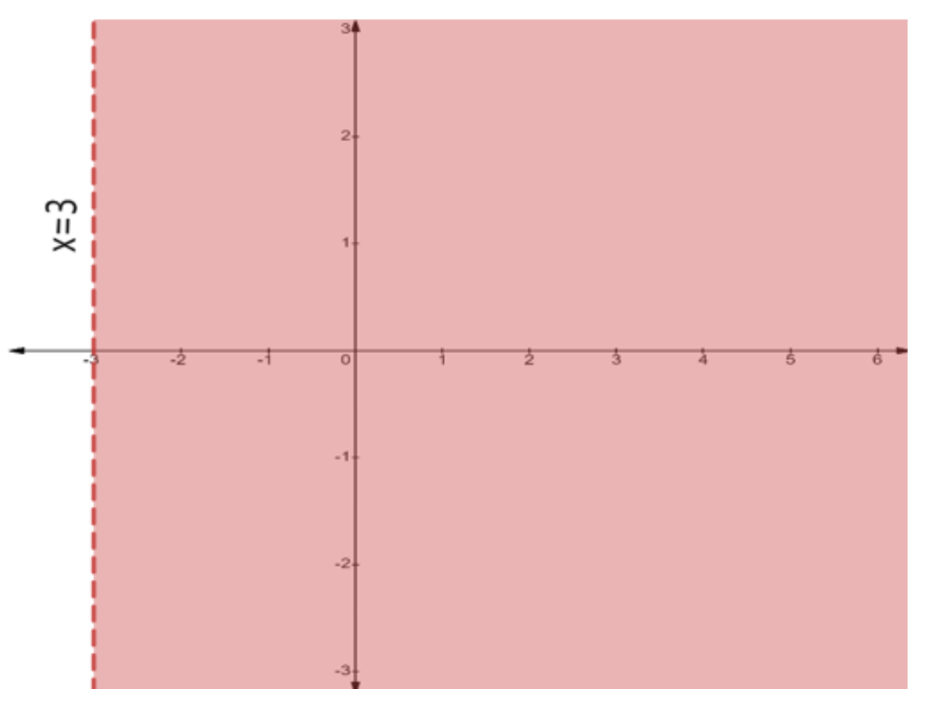
- Use a solid line for inequalities with ≤ or ≥, and a dashed line for inequalities with < or >. This indicates whether the points on the line are part of the solution.
- Next, select a test point (like (0,0)) not on the line to determine which side of the line represents the solution region for that inequality.
- Shade the corresponding region for each inequality.
- The final solution is the common shaded area that satisfies all the given inequalities simultaneously.
3. Why is it important to represent the solution of a linear inequality on a number line?
Representing the solution of a linear inequality in one variable on a number line is crucial because, unlike an equation which often has a single value as a solution, an inequality has a range of solutions. The number line provides a clear visual representation of this entire set of infinite values. It helps you understand the concept of a solution set, including whether the endpoints are included (closed circle) or excluded (open circle), making the abstract concept much more concrete.
4. What is the most common mistake students make when solving problems from Chapter 6, Linear Inequalities?
A very common mistake is forgetting to reverse the inequality sign when multiplying or dividing both sides of an inequality by a negative number. For instance, if you have -2x < 10 and divide by -2, the sign must flip, resulting in x > -5. The detailed NCERT solutions provided by Vedantu explicitly highlight this rule in relevant problems to help students avoid this critical error and build a strong conceptual foundation.
5. How do the NCERT Solutions for the Miscellaneous Exercise of Chapter 6 differ from the regular exercises?
The NCERT Solutions for the Miscellaneous Exercise of Linear Inequalities tackle more complex and Higher Order Thinking Skills (HOTS) problems. These questions often require applying multiple concepts learned throughout the chapter or involve more intricate real-world scenarios (word problems). The solutions for this section are particularly detailed, breaking down multi-step problems into a logical sequence to help students master advanced applications of linear inequalities.
6. How can the concepts from Class 11 Maths Chapter 6 be applied in real-world situations?
The principles of linear inequalities are fundamental in solving various real-world optimisation problems. For example, a company might use a system of inequalities to determine the number of units to produce to maximise profit while staying within budget and resource constraints. Similarly, in diet planning, inequalities can be used to create a meal plan that meets certain nutritional requirements (like minimum protein, maximum fat) while adhering to a cost limit. The NCERT solutions help build the foundational skills needed for these applications.
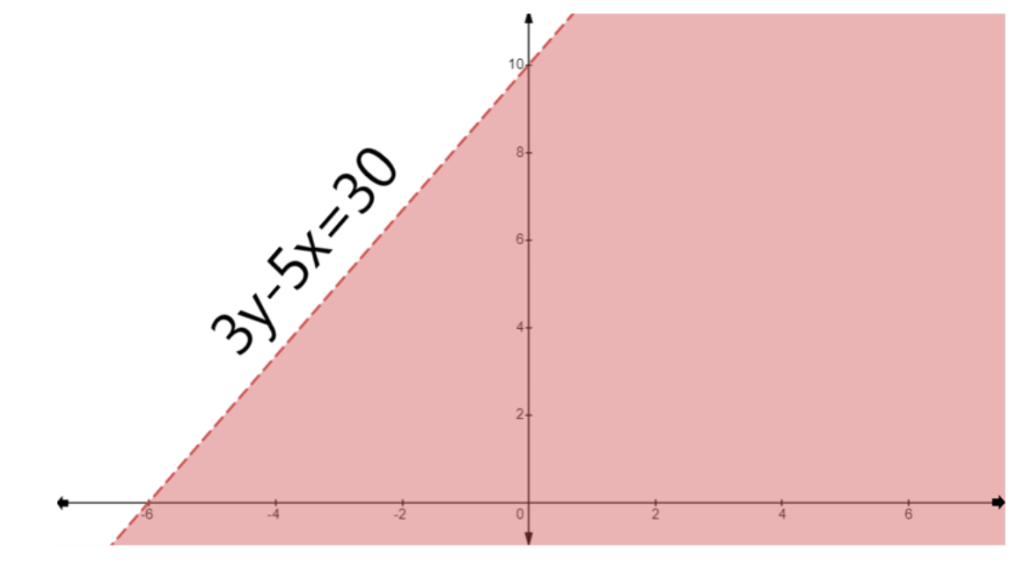
7. In graphical solutions, what is the significance of using a dashed line versus a solid line?
The type of line used in a graphical solution indicates whether the points on the line itself are part of the solution set. A solid line is used for slack inequalities (≤ or ≥), signifying that the values on the boundary line are included in the solution. A dashed line is used for strict inequalities (< or >), signifying that the values on the boundary line are not part of the solution. This distinction is critical for defining the solution region accurately, a detail that is carefully explained in the NCERT solutions.