Introduction To Three Dimensional Geometry Questions and Answers - Free PDF Download
In NCERT Solutions Class 11 Maths Chapter 11 Miscellaneous Exercise, you'll dive into the world of three-dimensional geometry! This chapter helps you learn how to find locations of points in 3D space, work with lines and planes, and understand the basics of direction ratios and cosines. If you get stuck on concepts or find 3D questions tricky, Vedantu’s step-by-step solutions will make things much easier to understand.
Table of Content
You’ll also come across important topics like finding midpoints, centroids, and applying formulas to solve higher-order problems. These NCERT solutions are available as free, downloadable PDFs so you can practice any time—even without the internet. If you want to check what’s included in the syllabus, the Class 11 Maths Syllabus has all the details.
Practicing with these solutions will boost your confidence and sharpen your 3D geometry skills for exams. Start with the exercises, and if you need more help, you can always use the detailed Class 11 Maths NCERT Solutions for every chapter.
Miscellaneous Exercise
1. Three vertices of a parallelogram $\text{ABCD}$ are $\text{A}\left( \text{3,-1,2} \right)$, $\text{B}\left( \text{1,2,-4} \right)$ and $\text{C}\left( \text{-1,1,2} \right)$. Find the coordinates of the fourth vertex.
Ans: We are given the three vertices of a parallelogram $\text{ABCD}$ are $\text{A}\left( \text{3,-1,2} \right)$, $\text{B}\left( \text{1,2,-4} \right)$ and $\text{C}\left( \text{-1,1,2} \right)$.
Let the coordinates of the fourth vertex of the parallelogram $\text{ABCD}$ be $\text{D}\left( \text{x,y,z} \right)$.
According to the property of a parallelogram, the diagonals of the parallelogram bisect each other.
In this parallelogram $\text{ABCD}$, $\text{AC}$ and $\text{BD}$ at point $\text{O}$.
So,
$\text{Mid-point of AC = Mid-point of BD}$
$\left( \frac{\text{3-1}}{\text{2}},\text{ }\frac{\text{-1+1}}{\text{2}},\text{ }\frac{\text{2+2}}{\text{2}} \right)\text{ = }\left( \frac{\text{x+1}}{\text{2}},\text{ }\frac{\text{y+1}}{\text{2}},\text{ }\frac{\text{z-4}}{\text{2}} \right)$
$\left( \text{1,0,2} \right)\text{ = }\left( \frac{\text{x+1}}{\text{2}},\text{ }\frac{\text{y+1}}{\text{2}},\text{ }\frac{\text{z-4}}{\text{2}} \right)$
$\frac{\text{x+1}}{\text{2}}\text{ = 1}$
$\frac{\text{y+2}}{\text{2}}\text{ = 0}$
$\frac{\text{z-4}}{\text{2}}\text{ = 2}$
We get, $\text{x = 1}$, $\text{y = 2}$ and $\text{z = 8}$
Therefore, the coordinates of the fourth vertex of the parallelogram $\text{ABCD}$ are $\text{D}\left( \text{1,-2,8} \right)$.
2. Find the lengths of the medians of the triangle with $\text{A}\left( \text{0,0,6} \right)$, $\text{B}\left( \text{0,4,0} \right)$ and $\text{C}\left( \text{6,0,0} \right)$.
Ans: For the given triangle $\text{ABC}$. Let $\text{AD}$, $\text{BE}$ and $\text{CF}$ are the medians:
We know that the median divides the line segment into two equal parts, so $\text{D}$ is the midpoint of $\text{BC}$, therefore,
$\text{Coordinates of point D = }\left( \frac{\text{0+6}}{\text{2}},\text{ }\frac{\text{4+0}}{\text{2}},\text{ }\frac{\text{0+0}}{\text{2}} \right)$
$\text{Coordinates of point D = }\left( \text{3,2,0} \right)$
$\text{AD = }\sqrt{{{\left( \text{0-3} \right)}^{\text{2}}}\text{+}{{\left( \text{0-2} \right)}^{\text{2}}}\text{+}{{\left( \text{6-0} \right)}^{\text{2}}}}$
$\text{AD = }\sqrt{\text{9+4+36}}$
$\text{AD = }\sqrt{\text{49}}$
$\text{AD = 7}$
Similarly, $\text{E}$ is the midpoint of $\text{AC}$,
$\text{Coordinates of point E = }\left( \frac{\text{0+6}}{\text{2}},\text{ }\frac{\text{0+0}}{\text{2}},\text{ }\frac{\text{0+6}}{\text{2}} \right)$
$\text{Coordinates of point E = }\left( \text{3,0,3} \right)$
$\text{AC = }\sqrt{{{\left( \text{3-0} \right)}^{\text{2}}}\text{+}{{\left( \text{0-4} \right)}^{\text{2}}}\text{+}{{\left( \text{3-0} \right)}^{\text{2}}}}$
$\text{AC = }\sqrt{\text{9+16+9}}$
$\text{AC = }\sqrt{\text{34}}$
Similarly, $\text{F}$ is the midpoint of $\text{AB}$,
$\text{Coordinates of point F = }\left( \frac{\text{0+0}}{\text{2}},\text{ }\frac{\text{0+4}}{\text{2}},\text{ }\frac{\text{6+0}}{\text{2}} \right)$
$\text{Coordinates of point F = }\left( \text{0,2,3} \right)$
$\text{CF = }\sqrt{{{\left( \text{6-0} \right)}^{\text{2}}}\text{+}{{\left( \text{0-2} \right)}^{\text{2}}}\text{+}{{\left( \text{0-3} \right)}^{\text{2}}}}$
$\text{CF = }\sqrt{\text{36+4+9}}$
$\text{CF = }\sqrt{\text{49}}$
$\text{CF = 7}$
Therefore, the lengths of the medians of the triangle $\text{ABC}$ we obtain are, $\text{7, }\sqrt{\text{34}}\text{, 7}$
3. If the origin is the centroid of the triangle $\text{PQR}$ with vertices $\text{P}\left( \text{2a,2,6} \right)$, $\text{Q}\left( \text{-4,3b,-10} \right)$ and $\text{R}\left( \text{8,14,2c} \right)$, then find the values of $\text{a}$, $\text{b}$ and $\text{c}$
Ans: The given triangle $\text{PQR}$
We know that the coordinates of the centroid of triangle with the vertices $\left( {{\text{x}}_{1}},{{\text{y}}_{1}},{{\text{z}}_{1}} \right)$, $\left( {{\text{x}}_{2}},{{\text{y}}_{2}},{{\text{z}}_{2}} \right)$ and $\left( {{\text{x}}_{3}},{{\text{y}}_{3}},{{\text{z}}_{3}} \right)$ are,
$\frac{{{\text{x}}_{\text{1}}}\text{+}{{\text{x}}_{\text{2}}}\text{+}{{\text{x}}_{\text{3}}}}{\text{3}}=\frac{{{\text{y}}_{\text{1}}}\text{+}{{\text{y}}_{\text{2}}}\text{+}{{\text{y}}_{\text{3}}}}{\text{3}}=\frac{{{\text{z}}_{\text{1}}}\text{+}{{\text{z}}_{\text{2}}}\text{+}{{\text{z}}_{\text{3}}}}{\text{3}}$
For triangle $\text{PQR}$, the coordinates will be,
$\text{ }\!\!\Delta\!\!\text{ PQR = }\frac{\text{2a-4+8}}{\text{3}}=\frac{\text{2+3b+14}}{\text{3}}=\frac{\text{6-10+2c}}{\text{3}}$
$\text{ }\!\!\Delta\!\!\text{ PQR = }\frac{\text{2a+4}}{\text{3}}=\frac{\text{3b+16}}{\text{3}}=\frac{\text{2c-4}}{\text{3}}$
Now, we are given that centroid is the origin,
$\frac{\text{2a+4}}{\text{3}}\text{ = 0}$
$\frac{\text{3b+16}}{\text{3}}\text{ = 0}$
$\frac{\text{2c-4}}{\text{3}}\text{ = 0}$
$\text{a = -2}$,
$\text{b = -}\frac{\text{16}}{\text{3}}$
$\text{c = 2}$
Therefore, we obtain the values as $\text{a = -2}$, $\text{b = -}\frac{\text{16}}{\text{3}}$ and $\text{c = 2}$.
4. If $\text{A}$ and $\text{B}$ be the points $\left( \text{3,4,5} \right)$ and $\left( \text{-1,3,-7} \right)$ respectively, find the equation of the set of points $\text{P}$ such that $\text{P}{{\text{A}}^{\text{2}}}\text{+P}{{\text{B}}^{\text{2}}}\text{ = }{{\text{k}}^{\text{2}}}$, where $\text{k}$ is a constant.
Ans: Let the coordinates of point $\text{P}$ be $\left( \text{x,y,z} \right)$.
Using the distance formula we get,
$\text{P}{{\text{A}}^{\text{2}}}\text{=}{{\left( \text{x-3} \right)}^{\text{2}}}\text{+}{{\left( \text{y-4} \right)}^{\text{2}}}\text{+}{{\left( \text{z-5} \right)}^{\text{2}}}$
$\text{P}{{\text{A}}^{\text{2}}}\text{ = }{{\text{x}}^{\text{2}}}\text{+9-6x+}{{\text{y}}^{\text{2}}}\text{+16-8y+}{{\text{z}}^{\text{2}}}\text{+25-10z}$
$\text{P}{{\text{A}}^{\text{2}}}\text{ = }{{\text{x}}^{\text{2}}}\text{-6x+}{{\text{y}}^{\text{2}}}\text{-8y+}{{\text{z}}^{\text{2}}}\text{-10z+50}$
Similarly,
$\text{P}{{\text{B}}^{\text{2}}}\text{ = }{{\left( \text{x-1} \right)}^{\text{2}}}\text{+}{{\left( \text{y-3} \right)}^{\text{2}}}\text{+}{{\left( \text{z-7} \right)}^{\text{2}}}$
$\text{P}{{\text{A}}^{\text{2}}}\text{ = }{{\text{x}}^{\text{2}}}\text{-2x+}{{\text{y}}^{\text{2}}}\text{-6y+}{{\text{z}}^{\text{2}}}\text{-14z+59}$
We are given that,
$\text{P}{{\text{A}}^{\text{2}}}\text{+P}{{\text{B}}^{\text{2}}}\text{ = }{{\text{k}}^{\text{2}}}$
So,
$\left( {{\text{x}}^{\text{2}}}\text{-6x+}{{\text{y}}^{\text{2}}}\text{-8y+}{{\text{z}}^{\text{2}}}\text{-10z+50} \right)\text{+}\left( {{\text{x}}^{\text{2}}}\text{-2x+}{{\text{y}}^{\text{2}}}\text{-6y+}{{\text{z}}^{\text{2}}}\text{-14z+59} \right)\text{ = }{{\text{k}}^{2}}$
$\text{2}{{\text{x}}^{\text{2}}}\text{+2}{{\text{y}}^{\text{2}}}\text{+2}{{\text{z}}^{\text{2}}}\text{-4x-14y+14z+109 =}\ {{\text{k}}^{\text{2}}}$
$\text{2}\left( {{\text{x}}^{\text{2}}}\text{+}{{\text{y}}^{\text{2}}}\text{+}{{\text{z}}^{\text{2}}}\text{-2x-7y+7z} \right)\text{ = }{{\text{k}}^{\text{2}}}\text{-109}$
${{\text{x}}^{\text{2}}}\text{+}{{\text{y}}^{\text{2}}}\text{+}{{\text{z}}^{\text{2}}}\text{-2x-7y+7z = }\frac{{{\text{k}}^{\text{2}}}\text{-109}}{\text{2}}$
Therefore, the equation is as follows ${{\text{x}}^{\text{2}}}\text{+}{{\text{y}}^{\text{2}}}\text{+}{{\text{z}}^{\text{2}}}\text{-2x-7y+2z = }\frac{{{\text{k}}^{\text{2}}}\text{-109}}{\text{2}}$
Conclusion
NCERT Solutions for Miscellaneous Exercise Class 11 Chapter 11 helps in understanding three-dimensional geometry. The Miscellaneous Exercise includes different types of problems that improve skills in 3D geometry. Practising these problems is important for doing well in exams and for future studies in Maths. These exercises help students gain confidence and become better at solving complex geometry questions.
Class 11 Maths Chapter 11: Exercises Breakdown
CBSE Class 11 Maths Chapter 11 Other Study Materials
Chapter-Specific NCERT Solutions for Class 11 Maths
Given below are the chapter-wise NCERT Solutions for Class 11 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.
Important Related Links for CBSE Class 11 Maths
FAQs on NCERT Solutions For Class 11 Maths Miscellaneous Exercise Chapter 11 Introduction To Three Dimensional Geometry - 2025-26
1. How are NCERT Solutions for Class 11 Maths Chapter 11 structured to help solve three-dimensional geometry problems step by step?
The NCERT Solutions for Class 11 Maths Chapter 11 are organised by type of problem, beginning with foundational concepts such as locating points in 3D space, and progressing to direction ratios, lines, and planes. Each question is solved using a step-by-step method that starts with identifying what is given and what needs to be found, choosing the correct formula, substituting values accurately, and completing calculations one step at a time for clarity and precision.
2. What methods are commonly used in NCERT Solutions for calculating the coordinates of a point in three-dimensional space?
To calculate coordinates in 3D, common methods include the distance formula (for finding the distance between two points), and the section formula (for finding a point dividing a line segment in a given ratio). The mid-point formula is also frequently applied for finding the midpoint of a segment. Mastering these techniques is essential for solving placement and division problems in 3D geometry.
3. Which common mistakes should be avoided while attempting NCERT Solutions of Class 11 Maths Chapter 11?
Some frequent mistakes to avoid include:
- Incorrectly substituting coordinate values in formulas
- Misunderstanding or omitting direction ratios
- Sign errors in algebraic calculations
- Forgetting the 3D context, leading to missed axes in solutions
Carefully double-check each calculation, especially when working with negative or decimal coordinates.
4. How do direction ratios and direction cosines differ, and why is this distinction important in solving 3D geometry questions?
Direction ratios describe the proportional direction of a line in 3D space and can be any multiple of a set of numbers. Direction cosines are the cosines of the angles that a line makes with the coordinate axes and are uniquely determined. Understanding this distinction is crucial because equations of lines require either, but only direction cosines are normalised and directly relate to spatial orientation.
5. In what ways does solving NCERT Solutions for Miscellaneous Exercises improve preparation for board exams and competitive tests?
Solving Miscellaneous Exercises from NCERT Solutions for Class 11 Maths Chapter 11 strengthens problem-solving skills, enhances analytical thinking, and provides a deeper understanding of complex spatial relationships and formulas. This thorough practice is key to answering higher-order and application-based questions seen in board and entrance exams.
6. How is the equation of a plane determined using NCERT Solutions methods in Chapter 11?
The equation of a plane in three-dimensional space is determined by knowing either a point on the plane and the normal vector to the plane, or three non-collinear points lying on the plane. Using these, the general form ax + by + cz + d = 0 is established and solved stepwise for required unknowns following the NCERT methodology.
7. Why is understanding the coordinate axes fundamental for working with 3D geometry in this chapter?
The x, y, and z axes form the basis of three-dimensional geometry, allowing precise location of any point in space. Grasping this framework is essential to visualise, develop equations, and interpret relationships between points, lines, and planes effectively in both academic and real-world contexts.
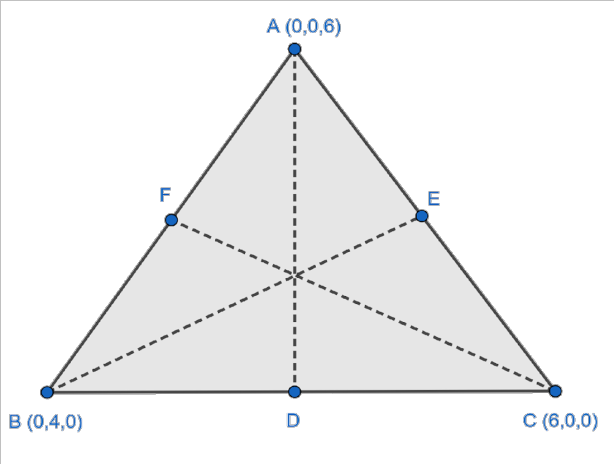
8. How can the concept of centroid be applied in NCERT Solutions problems involving three-dimensional triangles?
The centroid of a triangle in 3D is the average of the coordinates of its three vertices. This concept is used to solve problems involving balance, symmetry, and to determine unknown parameters when the centroid is given or needs to be found, employing the formula:
- Centroid = ((x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3, (z₁ + z₂ + z₃)/3)
Mastery of this idea is vital for several higher-order questions in the chapter.
9. What are the major types of problems covered in the Miscellaneous Exercise of Class 11 Maths Chapter 11 NCERT Solutions?
The Miscellaneous Exercise comprises a mix of questions on:
- Finding distances and midpoints
- Applying section and ratio formulas
- Working with direction ratios and cosines
- Formulating equations of lines and planes
- Application-based and HOTS (Higher Order Thinking Skills) problems
This diverse practice ensures a well-rounded grasp of three-dimensional geometry concepts.
10. How does the stepwise approach recommended in NCERT Solutions help in avoiding calculation errors in 3D geometry?
The recommended stepwise approach ensures that each formula is correctly applied, all substitutions are checked, and every calculation is performed methodically. This systematic process reduces confusion, especially in multi-step problems, and is particularly important when working with negative or fractional coordinates commonly found in Class 11 3D geometry problems.
