Maths Class 11 Chapter 10 Questions and Answers - Free PDF Download
FAQs on NCERT Solutions For Class 11 Maths Chapter 10 Conic Sections Exercise 10.1 (2025-26)
1. What are conic sections and how are they formed geometrically?
Conic sections are curves formed when a plane intersects a right circular cone at different angles. The four main types are circle, ellipse, parabola, and hyperbola, each created by varying the angle and position of the intersecting plane relative to the cone's axis.
2. How does the NCERT Solutions for exercise 10.1 class 11 conic sections help students understand these curves?
NCERT Solutions for exercise 10.1 provide step-by-step solutions to problems involving circles, parabolas, ellipses, and hyperbolas. Each solution demonstrates the application of standard equations and geometric properties with detailed working.
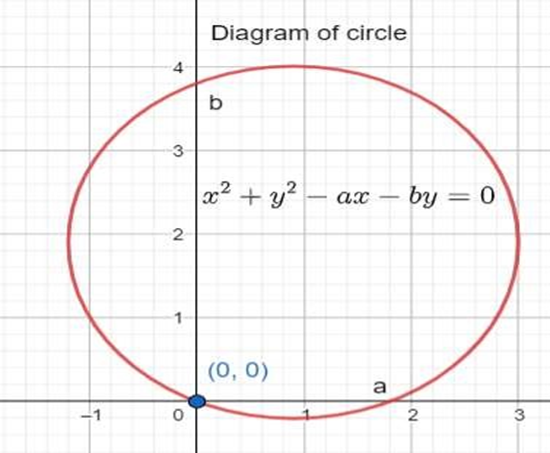
3. What is the general equation of a circle in coordinate geometry?
The general equation of a circle is (x-h)² + (y-k)² = r², where (h,k) represents the center coordinates and r is the radius. This can also be written in expanded form as x² + y² + 2gx + 2fy + c = 0.
4. Can students download the class 11 maths ex 10.1 conic sections solutions as a Free PDF?
Yes, students can access Free PDF downloads of ex 10.1 class 11 maths solutions through educational platforms like Vedantu. These PDFs contain complete worked solutions for all exercise problems with proper formatting and mathematical notation.
5. How do students identify different types of conic sections from their equations?
Students identify conic sections by examining the general second-degree equation Ax² + Bxy + Cy² + Dx + Ey + F = 0. The discriminant B² - 4AC determines the type: circle/ellipse (B² - 4AC < 0), parabola (B² - 4AC = 0), or hyperbola (B² - 4AC > 0).
6. What topics are covered in the 10.1 class 11 conic sections exercise?
Exercise 10.1 focuses primarily on circles as the introductory conic section. Problems involve finding equations of circles given different conditions like center-radius, diameter endpoints, or points on the circumference.
Mastering circle problems builds the foundation for understanding more complex conics like ellipses, parabolas, and hyperbolas in subsequent exercises.
7. Why is the standard form of a parabola important in coordinate geometry?
The standard form y² = 4ax represents a parabola opening rightward with vertex at origin and focus at (a,0). This form simplifies calculations for finding focus, directrix, and solving problems involving parabolic curves in coordinate geometry applications.
8. How do exercise 10.1 class 11 conic sections answers help with exam preparation?
The exercise 10.1 answers provide detailed solutions with complete working steps, helping students understand problem-solving techniques for circle-related questions that frequently appear in board exams.
9. What is the relationship between the focus and directrix of a parabola?
For any point on a parabola, the distance to the focus equals the distance to the directrix. This constant ratio property defines the parabola and helps derive its equation in coordinate geometry applications.
10. How does the ex 10.1 class 11 conic section solutions PDF support different learning styles?
The PDF format presents solutions through multiple representations including algebraic steps, geometric diagrams, and coordinate plotting, catering to visual, analytical, and kinesthetic learning preferences.