NCERT Solutions For Class 10 Maths Chapter 8 Introduction To Trigonometry - 2025-26

Exercise 8.1 - In this exercise, students are introduced to the basic trigonometric ratios - sine, cosine, and tangent, and their reciprocal functions. They learn how to find the values of these ratios for acute angles in a right triangle. The exercise also covers the concept of trigonometric identities, which are fundamental relationships between trigonometric functions.

Exercise 8.2 - This exercise deals with the application of trigonometric ratios to solve real-life problems. Students learn how to use trigonometric ratios to find the height and distance of an object, as well as the angle of elevation and depression. They also learn how to use the Pythagorean theorem to solve problems involving right triangles.

Exercise 8.3 - The final exercise covers the concept of trigonometric equations. Students learn how to solve trigonometric equations using the identities and ratios learned in the previous exercises. They also learn how to find the general solution of a trigonometric equation, which involves finding all the possible solutions. Finally, the exercise covers the concept of the period of a trigonometric function and how to find it for different functions.

Access NCERT Solutions for Class 10 Maths Chapter 8 – Introduction to Trigonometry

Exercise 8.1 

1. In $\Delta ABC$ right angled at $B$, $AB=24\text{ cm}$, $BC=7\text{ cm}$. Determine 

(i) $\sin A,\cos A$ 

Ans: Given that in the right angle triangle $\Delta ABC$, $AB=24\text{ cm}$, $BC=7\text{ cm}$.

Let us draw a right triangle $\Delta ABC$, also $AB=24\text{ cm}$, $BC=7\text{ cm}$. We get

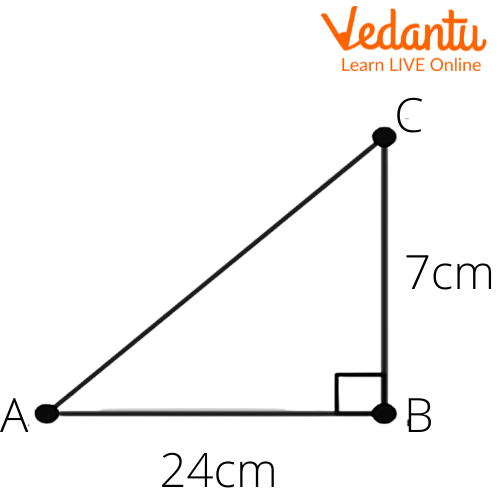
We have to find $\sin A,\cos A$.

We know that for right triangle

$\sin \theta =\dfrac{\text{opposite side}}{\text{hypotenuse}}$ and 

$\cos \theta =\dfrac{\text{adjacent side}}{\text{hypotenuse}}$

Now, we need to apply the Pythagoras theorem to find the measure of hypotenuse.

In $\Delta ABC$, by Pythagoras theorem ,

${{\left( \text{hypotenuse} \right)}^{2}}={{\left( base \right)}^{2}}+{{\left( perpendicular \right)}^{2}}$ 

Here, $AB=24\text{ cm}$, $BC=7\text{ cm}$

We get

$\Rightarrow {{\left( \text{AC} \right)}^{2}}={{\left( AB \right)}^{2}}+{{\left( BC \right)}^{2}}$ 

$\Rightarrow {{\left( \text{AC} \right)}^{2}}={{\left( 24 \right)}^{2}}+{{\left( 7 \right)}^{2}}$

$\Rightarrow {{\left( \text{AC} \right)}^{2}}=576+49$

$\Rightarrow {{\left( \text{AC} \right)}^{2}}=625\text{ }c{{m}^{2}}$

$\Rightarrow AC=25\text{ cm}$ 

Now, 

$\sin \theta =\dfrac{\text{opposite side}}{\text{hypotenuse}}$ 

$\Rightarrow \sin A=\dfrac{BC}{AC}$ 

$\therefore \sin A=\dfrac{7}{25}$

$\cos \theta =\dfrac{\text{adjacent side}}{\text{hypotenuse}}$

$\Rightarrow \cos A=\dfrac{AB}{AC}$

$\therefore \cos A=\dfrac{24}{25}$

(ii) $\sin C,\cos C$ 

Ans: Given that in the right angle triangle $\Delta ABC$, $AB=24\text{ cm}$, $BC=7\text{ cm}$.

Let us draw a right triangle $\Delta ABC$, also $AB=24\text{ cm}$, $BC=7\text{ cm}$. We get

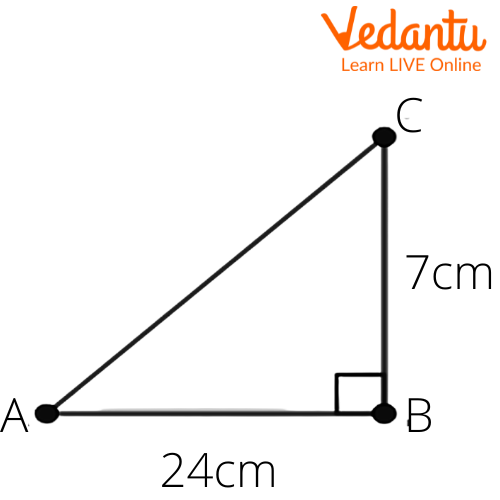
We have to find $\sin C,\cos C$.

We know that for right triangle

$\sin \theta =\dfrac{\text{opposite side}}{\text{hypotenuse}}$ and 

$\cos \theta =\dfrac{\text{adjacent side}}{\text{hypotenuse}}$

Now, we need to apply the Pythagoras theorem to find the measure of hypotenuse.

In $\Delta ABC$, by Pythagoras theorem ,

${{\left( \text{hypotenuse} \right)}^{2}}={{\left( base \right)}^{2}}+{{\left( perpendicular \right)}^{2}}$ 

Here, $AB=24\text{ cm}$, $BC=7\text{ cm}$

We get

$\Rightarrow {{\left( \text{AC} \right)}^{2}}={{\left( AB \right)}^{2}}+{{\left( BC \right)}^{2}}$ 

$\Rightarrow {{\left( \text{AC} \right)}^{2}}={{\left( 24 \right)}^{2}}+{{\left( 7 \right)}^{2}}$

$\Rightarrow {{\left( \text{AC} \right)}^{2}}=576+49$

$\Rightarrow {{\left( \text{AC} \right)}^{2}}=625\text{ }c{{m}^{2}}$

$\Rightarrow AC=25\text{ cm}$

Now, 

$\sin \theta =\dfrac{\text{opposite side}}{\text{hypotenuse}}$ 

$\Rightarrow \sin C=\dfrac{AB}{AC}$ 

$\therefore \sin C=\dfrac{24}{25}$

$\cos \theta =\dfrac{\text{adjacent side}}{\text{hypotenuse}}$

$\Rightarrow \cos C=\dfrac{BC}{AC}$

$\therefore \cos A=\dfrac{7}{25}$

3. In the given figure find $\tan P-\cot R$.

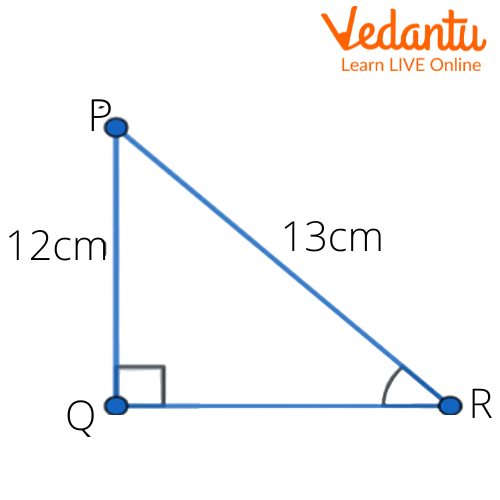
Ans: Given in the figure, 

$PQ=12\text{ cm}$ 

$PQ=13\text{ cm}$

We know that for right triangle

$\tan \theta =\dfrac{\text{opposite side}}{\text{adjacent side}}$ and 

$\cot \theta =\dfrac{\text{adjacent side}}{\text{opposite side}}$

Now, we need to apply the Pythagoras theorem to find the measure of adjacent side/base.

In $\Delta PQR$, by Pythagoras theorem ,

${{\left( \text{hypotenuse} \right)}^{2}}={{\left( base \right)}^{2}}+{{\left( perpendicular \right)}^{2}}$ 

We get

$\Rightarrow {{\left( PR \right)}^{2}}={{\left( PQ \right)}^{2}}+{{\left( QR \right)}^{2}}$ 

$\Rightarrow {{\left( 13 \right)}^{2}}={{\left( 12 \right)}^{2}}+{{\left( QR \right)}^{2}}$

$\Rightarrow 169=144+{{\left( QR \right)}^{2}}$

$\Rightarrow {{\left( QR \right)}^{2}}=169-144$

$\Rightarrow {{\left( QR \right)}^{2}}=25\text{ }c{{m}^{2}}$

$\Rightarrow QR=5\text{ cm}$ 

Now, 

$\tan P=\dfrac{\text{opposite side}}{\text{adjacent side}}$ 

$\Rightarrow \tan P=\dfrac{QR}{PQ}$ 

$\therefore \tan P=\dfrac{5}{12}$

$\cot R=\dfrac{\text{adjacent side}}{\text{opposite side}}$

$\Rightarrow \cot R=\dfrac{QR}{PQ}$

$\therefore \cot R=\dfrac{5}{12}$

$\Rightarrow \tan P-\cot R=\dfrac{5}{12}-\dfrac{5}{12}$

$\therefore \tan P-\cot R=0$ 

3. If $\sin A=\dfrac{3}{4}$, calculate $\cos A$ and $\tan A$.

Ans: Let us consider a right angled triangle $\Delta ABC$. We get

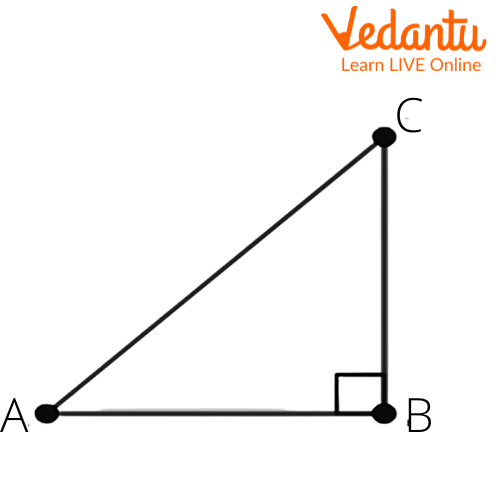
Given that $\sin A=\dfrac{3}{4}$.

We know that  $\sin \theta =\dfrac{\text{opposite side}}{\text{hypotenuse}}$.

From the above figure, we get

$\sin A=\dfrac{BC}{AC}$

Therefore, we get

$\Rightarrow BC=3$ and

$\Rightarrow AC=4$ 

Now, we have to find the values of $\cos A$ and $\tan A$.

We know that $\cos \theta =\dfrac{\text{adjacent side}}{\text{hypotenuse}}$ and $\tan \theta =\dfrac{\text{opposite side}}{\text{adjacent side}}$.

Now, we need to apply the Pythagoras theorem to find the measure of adjacent side/base.

In $\Delta ABC$, by Pythagoras theorem ,

${{\left( \text{hypotenuse} \right)}^{2}}={{\left( base \right)}^{2}}+{{\left( perpendicular \right)}^{2}}$ 

Here, $AC=4\text{ cm}$, $BC=3\text{ cm}$

We get

$\Rightarrow {{\left( \text{AC} \right)}^{2}}={{\left( AB \right)}^{2}}+{{\left( BC \right)}^{2}}$ 

$\Rightarrow {{4}^{2}}=A{{B}^{2}}+{{3}^{2}}$

$\Rightarrow 16=A{{B}^{2}}+9$

$\Rightarrow A{{B}^{2}}=16-9$

$\Rightarrow A{{B}^{2}}=7$

$\Rightarrow AB=\sqrt{7}\text{ cm}$

Now, we get

$\cos A=\dfrac{AB}{AC}$ 

$\therefore \cos A=\dfrac{\sqrt{7}}{4}$ 

And $\tan A=\dfrac{BC}{AB}$

$\therefore \tan A=\dfrac{3}{\sqrt{7}}$

4. Given $15\cot A=8$. Find $\sin A$ and $\sec A$.

Ans: Let us consider a right angled triangle $\Delta ABC$. We get

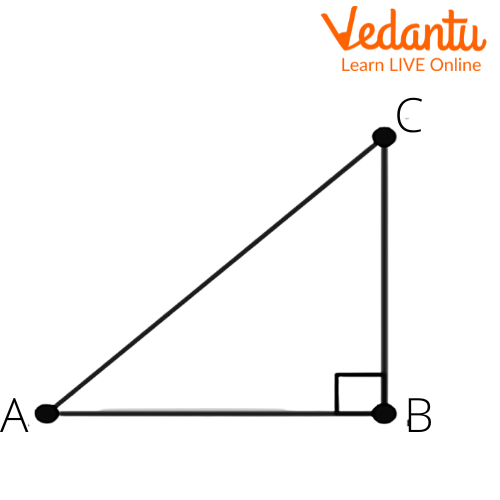
Given that $15\cot A=8$.

We get $\cot A=\dfrac{8}{15}$.

We know that $\cot \theta =\dfrac{\text{adjacent side}}{\text{opposite side}}$.

From the above figure, we get

$\cot A=\dfrac{AB}{BC}$

Therefore, we get

$\Rightarrow BC=15$ and

$\Rightarrow AB=8$ 

Now, we have to find the values of $\sin A$ and $\sec A$.

We know that $\sin \theta =\dfrac{\text{opposite side}}{\text{hypotenuse}}$ and $\sec \theta =\dfrac{\text{hypotenuse}}{\text{adjacent side}}$.

Now, we need to apply the Pythagoras theorem to find the measure of hypotenuse.

In $\Delta ABC$, by Pythagoras theorem ,

${{\left( \text{hypotenuse} \right)}^{2}}={{\left( base \right)}^{2}}+{{\left( perpendicular \right)}^{2}}$ 

We get

$\Rightarrow {{\left( \text{AC} \right)}^{2}}={{\left( AB \right)}^{2}}+{{\left( BC \right)}^{2}}$ 

$\Rightarrow A{{C}^{2}}={{8}^{2}}+{{15}^{2}}$

$\Rightarrow A{{C}^{2}}=64+225$

$\Rightarrow A{{C}^{2}}=289$

$\Rightarrow AC=17\text{ cm}$

Now, we get

$\sin A=\dfrac{BC}{AC}$ 

$\therefore \sin A=\dfrac{15}{17}$ 

And $\sec A=\dfrac{AC}{AB}$

$\therefore \sec A=\dfrac{17}{8}$

5. Given $\sec \theta =\dfrac{13}{12}$, calculate all other trigonometric ratios.

Ans: Let us consider a right angled triangle $\Delta ABC$. We get

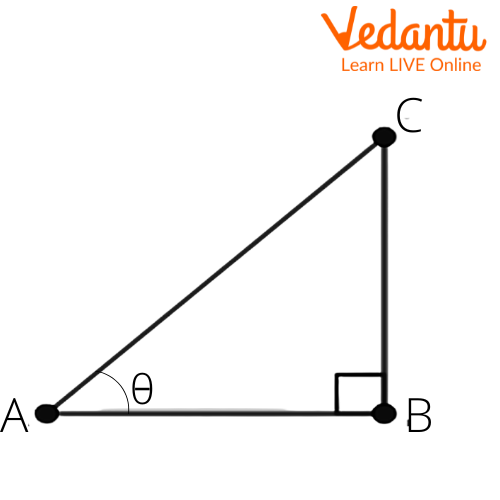
Given that $\sec \theta =\dfrac{13}{12}$.

We know that $\sec \theta =\dfrac{\text{hypotenuse}}{\text{adjacent side}}$.

From the above figure, we get

$\sec \theta =\dfrac{AC}{AB}$

Therefore, we get

$\Rightarrow AC=13$ and

$\Rightarrow AB=12$ 

Now, we need to apply the Pythagoras theorem to find the measure of the perpendicular/opposite side.

In $\Delta ABC$, by Pythagoras theorem ,

${{\left( \text{hypotenuse} \right)}^{2}}={{\left( base \right)}^{2}}+{{\left( perpendicular \right)}^{2}}$ 

We get

$\Rightarrow {{\left( \text{AC} \right)}^{2}}={{\left( AB \right)}^{2}}+{{\left( BC \right)}^{2}}$ 

$\Rightarrow {{13}^{2}}={{12}^{2}}+B{{C}^{2}}$

$\Rightarrow 169=144+B{{C}^{2}}$

$\Rightarrow B{{C}^{2}}=25$

$\Rightarrow BC=5\text{ cm}$

Now, we know that

$\sin \theta =\dfrac{\text{opposite side}}{\text{hypotenuse}}$

Here, $\sin \theta =\dfrac{BC}{AC}$ 

$\therefore \sin \theta =\dfrac{5}{13}$ 

We know that $\cos \theta =\dfrac{\text{adjacent side}}{\text{hypotenuse}}$

Here, $\cos \theta =\dfrac{AB}{AC}$ 

$\therefore \cos \theta =\dfrac{12}{13}$

We know that $\tan \theta =\dfrac{\text{opposite side}}{\text{adjacent side}}$

Here, $\tan \theta =\dfrac{BC}{AB}$ 

$\therefore \tan \theta =\dfrac{5}{12}$

We know that $\operatorname{cosec}\theta =\dfrac{\text{hypotenuse}}{\text{opposite side}}$

Here, $\operatorname{cosec}\theta =\dfrac{AC}{BC}$

$\therefore \operatorname{cosec}\theta =\dfrac{13}{5}$

We know that $\cot \theta =\dfrac{\text{adjacent side}}{\text{opposite side}}$

Here, $\cot \theta =\dfrac{\text{AB}}{BC}$

\[\therefore \cot \theta =\dfrac{12}{5}\] .

6. If $\angle A$ and $\angle B$ are acute angles such that $\cos A=\cos B$, then show that $\angle A=\angle B$.

Ans: Let us consider a right angled triangle $\Delta ABC$. We get

Given that $\cos A=\cos B$.

In a right triangle $\Delta ABC$, we know that 

$\cos \theta =\dfrac{\text{adjacent side}}{\text{hypotenuse}}$

Here, 

$\cos A=\dfrac{AC}{AB}$ 

And $\cos B=\dfrac{BC}{AB}$ 

As given $\cos A=\cos B$, we get

$\Rightarrow \dfrac{AC}{AB}=\dfrac{BC}{AB}$ 

$\Rightarrow AC=AB$ 

Now, we know that angles opposite to the equal sides are also equal in measure.

Then, we get

$\angle A=\angle B$ 

Hence proved.

7. Evaluate the following if $\cot \theta =\dfrac{7}{8}$

(i) $\dfrac{\left( 1+\sin \theta  \right)\left( 1-\sin \theta  \right)}{\left( 1+\cos \theta  \right)\left( 1-\cos \theta  \right)}$ 

Ans: Let us consider a right angled triangle $\Delta ABC$. We get

Now, in a right triangle we know that $\cot \theta =\dfrac{\text{adjacent side}}{\text{opposite side}}$.

Here, from the figure $\cot \theta =\dfrac{BC}{AB}$ .

We get

$AB=8$ and 

$BC=7$ 

Now, we need to apply the Pythagoras theorem to find the measure of hypotenuse.

In $\Delta ABC$, by Pythagoras theorem ,

${{\left( \text{hypotenuse} \right)}^{2}}={{\left( base \right)}^{2}}+{{\left( perpendicular \right)}^{2}}$ 

We get

$\Rightarrow {{\left( \text{AC} \right)}^{2}}={{\left( AB \right)}^{2}}+{{\left( BC \right)}^{2}}$ 

$\Rightarrow {{\left( \text{AC} \right)}^{2}}={{8}^{2}}+{{7}^{2}}$

$\Rightarrow {{\left( \text{AC} \right)}^{2}}=64+49$

$\Rightarrow {{\left( \text{AC} \right)}^{2}}=113$

$\Rightarrow AC=\sqrt{113}$ 

Now, we know that 

$\sin \theta =\dfrac{\text{opposite side}}{\text{hypotenuse}}$

Here, we get

$\sin \theta =\dfrac{AB}{AC}=\dfrac{8}{\sqrt{113}}$ and 

$\cos \theta =\dfrac{\text{adjacent side}}{\text{hypotenuse}}$

Here, we get

$\cos \theta =\dfrac{BC}{AC}=\dfrac{7}{\sqrt{113}}$ 

Now, we have to evaluate 

$\dfrac{\left( 1+\sin \theta  \right)\left( 1-\sin \theta  \right)}{\left( 1+\cos \theta  \right)\left( 1-\cos \theta  \right)}$

Applying the identity $\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}$, we get

\[\Rightarrow \dfrac{\left( 1+\sin \theta  \right)\left( 1-\sin \theta  \right)}{\left( 1+\cos \theta  \right)\left( 1-\cos \theta  \right)}=\dfrac{1-{{\sin }^{2}}\theta }{1-{{\cos }^{2}}\theta }\] 

Substituting the values, we get

\[\Rightarrow \dfrac{\left( 1+\sin \theta  \right)\left( 1-\sin \theta  \right)}{\left( 1+\cos \theta  \right)\left( 1-\cos \theta  \right)}=\dfrac{1-{{\left( \dfrac{8}{\sqrt{113}} \right)}^{2}}}{1-{{\left( \dfrac{7}{\sqrt{113}} \right)}^{2}}}\]

\[\Rightarrow \dfrac{\left( 1+\sin \theta  \right)\left( 1-\sin \theta  \right)}{\left( 1+\cos \theta  \right)\left( 1-\cos \theta  \right)}=\dfrac{1-\dfrac{64}{113}}{1-\dfrac{49}{113}}\]

\[\Rightarrow \dfrac{\left( 1+\sin \theta  \right)\left( 1-\sin \theta  \right)}{\left( 1+\cos \theta  \right)\left( 1-\cos \theta  \right)}=\dfrac{\dfrac{113-64}{113}}{\dfrac{113-49}{113}}\]

\[\Rightarrow \dfrac{\left( 1+\sin \theta  \right)\left( 1-\sin \theta  \right)}{\left( 1+\cos \theta  \right)\left( 1-\cos \theta  \right)}=\dfrac{\dfrac{49}{113}}{\dfrac{64}{113}}\]

\[\therefore \dfrac{\left( 1+\sin \theta  \right)\left( 1-\sin \theta  \right)}{\left( 1+\cos \theta  \right)\left( 1-\cos \theta  \right)}=\dfrac{49}{64}\]

(ii) ${{\cot }^{2}}\theta $ 

Ans: Given that $\cot \theta =\dfrac{7}{8}$.

Now, ${{\cot }^{2}}\theta ={{\left( \dfrac{7}{8} \right)}^{2}}$

$\therefore {{\cot }^{2}}\theta =\dfrac{49}{64}$ 

8. If $3\cot A=4$, check whether $\dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}={{\cos }^{2}}A-{{\sin }^{2}}A$ or not.

Ans: Let us consider a right angled triangle $\Delta ABC$. We get

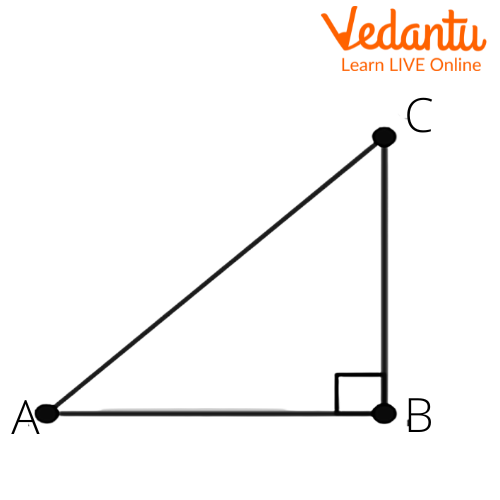
Given that $3\cot A=4$.

We get $\cot A=\dfrac{4}{3}$.

We know that $\cot \theta =\dfrac{\text{adjacent side}}{\text{opposite side}}$.

From the above figure, we get

$\cot A=\dfrac{AB}{BC}$

Therefore, we get

$\Rightarrow BC=3$ and

$\Rightarrow AB=4$ 

Now, we need to apply the Pythagoras theorem to find the measure of hypotenuse.

In $\Delta ABC$, by Pythagoras theorem ,

${{\left( \text{hypotenuse} \right)}^{2}}={{\left( base \right)}^{2}}+{{\left( perpendicular \right)}^{2}}$ 

We get

$\Rightarrow {{\left( \text{AC} \right)}^{2}}={{\left( AB \right)}^{2}}+{{\left( BC \right)}^{2}}$ 

$\Rightarrow A{{C}^{2}}={{4}^{2}}+{{3}^{2}}$

$\Rightarrow A{{C}^{2}}=16+9$

$\Rightarrow A{{C}^{2}}=25$

$\Rightarrow AC=5$

Now, let us consider LHS of the expression $\dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}={{\cos }^{2}}A-{{\sin }^{2}}A$, we get

$LHS=\dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}$

Now, we know that $\tan \theta =\dfrac{\text{opposite side}}{\text{adjacent side}}$

Here, we get

$\tan A=\dfrac{BC}{AB}=\dfrac{3}{4}$ 

Substitute the value, we get

$\Rightarrow \dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}=\dfrac{1-{{\left( \dfrac{3}{4} \right)}^{2}}}{1+{{\left( \dfrac{3}{4} \right)}^{2}}}$

$\Rightarrow \dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}=\dfrac{1-\dfrac{9}{16}}{1+\dfrac{9}{16}}$

$\Rightarrow \dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}=\dfrac{\dfrac{16-9}{16}}{\dfrac{16+9}{16}}$

$\Rightarrow \dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}=\dfrac{\dfrac{7}{16}}{\dfrac{25}{16}}$

$\Rightarrow \dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}=\dfrac{7}{25}$

Now, let us consider RHS of the expression $\dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}={{\cos }^{2}}A-{{\sin }^{2}}A$, we get

$RHS={{\cos }^{2}}A-{{\sin }^{2}}A$

We know that $\sin \theta =\dfrac{\text{opposite side}}{\text{hypotenuse}}$ and $\cos \theta =\dfrac{\text{adjacent side}}{\text{hypotenuse}}$.

Here, we get

$\sin A=\dfrac{BC}{AC}=\dfrac{3}{5}$  

And $\cos A=\dfrac{AB}{AC}=\dfrac{4}{5}$

Substitute the values, we get

$\Rightarrow {{\cos }^{2}}A-{{\sin }^{2}}A={{\left( \dfrac{4}{5} \right)}^{2}}-{{\left( \dfrac{3}{5} \right)}^{2}}$

$\Rightarrow {{\cos }^{2}}A-{{\sin }^{2}}A=\dfrac{16}{25}-\dfrac{9}{25}$

$\Rightarrow {{\cos }^{2}}A-{{\sin }^{2}}A=\dfrac{7}{25}$

Hence, we get LHS=RHS

$\therefore \dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}={{\cos }^{2}}A-{{\sin }^{2}}A$.

9. In $ABC$, right angled at $B$. If $\tan A=\dfrac{1}{\sqrt{3}}$, find the value of 

(i) $\sin A\cos C+\cos A\sin C$ 

Ans: Let us consider a right angled triangle $\Delta ABC$. We get

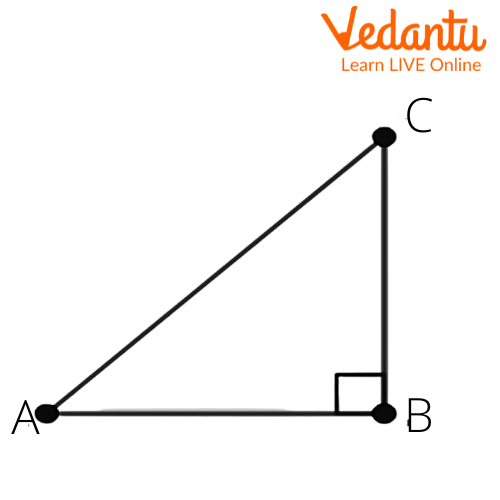
Given that $\tan A=\dfrac{1}{\sqrt{3}}$.

In a right triangle, we know that $\tan \theta =\dfrac{\text{opposite side}}{\text{adjacent side}}$

Here, from the figure we get

$\tan A=\dfrac{BC}{AB}=\dfrac{1}{\sqrt{3}}$

We get $BC=1$ and $AB=\sqrt{3}$ .

Now, we need to apply the Pythagoras theorem to find the measure of hypotenuse.

In $\Delta ABC$, by Pythagoras theorem ,

${{\left( \text{hypotenuse} \right)}^{2}}={{\left( base \right)}^{2}}+{{\left( perpendicular \right)}^{2}}$ 

We get

$\Rightarrow {{\left( \text{AC} \right)}^{2}}={{\left( AB \right)}^{2}}+{{\left( BC \right)}^{2}}$ 

$\Rightarrow A{{C}^{2}}={{\left( \sqrt{3} \right)}^{2}}+{{1}^{2}}$

$\Rightarrow A{{C}^{2}}=3+1$

$\Rightarrow A{{C}^{2}}=4$

$\Rightarrow AC=2$

We know that $\sin \theta =\dfrac{\text{opposite side}}{\text{hypotenuse}}$ and $\cos \theta =\dfrac{\text{adjacent side}}{\text{hypotenuse}}$.

Here, we get

$\sin A=\dfrac{BC}{AC}=\dfrac{1}{2}$  and $\sin C=\dfrac{AB}{AC}=\dfrac{\sqrt{3}}{2}$

And $\cos A=\dfrac{AB}{AC}=\dfrac{\sqrt{3}}{2}$and $\cos C=\dfrac{BC}{AC}=\dfrac{1}{2}$

Now, we have to find the value of the expression $\sin A\cos C+\cos A\sin C$.

Substituting the values we get

$\Rightarrow \sin A\cos C+\cos A\sin C=\dfrac{1}{2}\times \dfrac{1}{2}+\dfrac{\sqrt{3}}{2}\times \dfrac{\sqrt{3}}{2}$ 

$\Rightarrow \sin A\cos C+\cos A\sin C=\dfrac{1}{4}+\dfrac{3}{4}$

$\Rightarrow \sin A\cos C+\cos A\sin C=\dfrac{4}{4}$

$\therefore \sin A\cos C+\cos A\sin C=1$

(ii) $\cos A\cos C-\sin A\sin C$

Ans: Let us consider a right angled triangle $\Delta ABC$. We get

Given that $\tan A=\dfrac{1}{\sqrt{3}}$.

In a right triangle, we know that $\tan \theta =\dfrac{\text{opposite side}}{\text{adjacent side}}$

Here, from the figure we get

$\tan A=\dfrac{BC}{AB}=\dfrac{1}{\sqrt{3}}$

We get $BC=1$ and $AB=\sqrt{3}$ .

Now, we need to apply the Pythagoras theorem to find the measure of hypotenuse.

In $\Delta ABC$, by Pythagoras theorem ,

${{\left( \text{hypotenuse} \right)}^{2}}={{\left( base \right)}^{2}}+{{\left( perpendicular \right)}^{2}}$ 

We get

$\Rightarrow {{\left( \text{AC} \right)}^{2}}={{\left( AB \right)}^{2}}+{{\left( BC \right)}^{2}}$ 

$\Rightarrow A{{C}^{2}}={{\left( \sqrt{3} \right)}^{2}}+{{1}^{2}}$

$\Rightarrow A{{C}^{2}}=3+1$

$\Rightarrow A{{C}^{2}}=4$

$\Rightarrow AC=2$

We know that $\sin \theta =\dfrac{\text{opposite side}}{\text{hypotenuse}}$ and $\cos \theta =\dfrac{\text{adjacent side}}{\text{hypotenuse}}$.

Here, we get

$\sin A=\dfrac{BC}{AC}=\dfrac{1}{2}$  and $\sin C=\dfrac{AB}{AC}=\dfrac{\sqrt{3}}{2}$

And $\cos A=\dfrac{AB}{AC}=\dfrac{\sqrt{3}}{2}$and $\cos C=\dfrac{BC}{AC}=\dfrac{1}{2}$

Now, we have to find the value of the expression $\cos A\cos C-\sin A\sin C$.

Substituting the values we get

$\Rightarrow \cos A\cos C-\sin A\sin C=\dfrac{\sqrt{3}}{2}\times \dfrac{1}{2}-\dfrac{1}{2}\times \dfrac{\sqrt{3}}{2}$ 

$\Rightarrow \cos A\cos C-\sin A\sin C=\dfrac{\sqrt{3}}{4}-\dfrac{\sqrt{3}}{4}$

$\therefore \Rightarrow \cos A\cos C-\sin A\sin C=0$

10. In $\Delta PQR$, right angled at $Q$, $PR+QR=25\text{ cm}$ and $PQ=5\text{ cm}$. Determine the values of $\sin P,\cos P$ and $\tan P$.

Ans: Let us consider a right angled triangle $\Delta PQR$, we get

Given that $PR+QR=25\text{ cm}$ and $PQ=5\text{ cm}$.

Let $QR=25-PR$

Now, applying the Pythagoras theorem in $\Delta PQR$, we get

${{\left( \text{hypotenuse} \right)}^{2}}={{\left( base \right)}^{2}}+{{\left( perpendicular \right)}^{2}}$ 

We get

$\Rightarrow {{\left( PR \right)}^{2}}={{\left( PQ \right)}^{2}}+{{\left( QR \right)}^{2}}$ 

$\Rightarrow P{{R}^{2}}={{5}^{2}}+{{\left( 25-PR \right)}^{2}}$

$\Rightarrow P{{R}^{2}}=25+{{25}^{2}}+P{{R}^{2}}-50PR$

$\Rightarrow P{{R}^{2}}=P{{R}^{2}}+25+625-50PR$

$\Rightarrow 50PR=650$

$\Rightarrow PR=13\text{ cm}$ 

Therefore, 

$QR=25-13$

$\Rightarrow QR=12\text{ cm}$ 

Now, we know that in right triangle,

$\sin \theta =\dfrac{\text{opposite side}}{\text{hypotenuse}}$, $\cos \theta =\dfrac{\text{adjacent side}}{\text{hypotenuse}}$ and $\tan \theta =\dfrac{\text{opposite side}}{\text{adjacent side}}$.

Here, we get

$\sin P=\dfrac{QR}{PR}$ 

$\therefore \sin P=\dfrac{12}{13}$ 

$\cos P=\dfrac{PQ}{PR}$ 

$\therefore \cos P=\dfrac{5}{13}$ 

$\tan P=\dfrac{QR}{PQ}$ 

$\therefore \tan P=\dfrac{12}{5}$

11. State whether the following are true or false. Justify your answer.

(i) The value of $\tan A$ is always less than $1$.

Ans: The given statement is false. The value of $\tan A$ depends on the length of sides of a right triangle and sides of a triangle may have any measure.

(ii) For some value of angle $A$, $\sec A=\dfrac{12}{5}$.

Ans: We know that in the right triangle $\sec A=\dfrac{\text{hypotenuse}}{\text{adjacent side of }\angle \text{A}}$ .

We know that in the right triangle the hypotenuse is the largest side.

Therefore, the value of $\sec A$ must be greater than $1$.

In the given statement $\sec A=\dfrac{12}{5}$, which is greater than $1$.

Therefore, the given statement is true.

(iii) $\cos A$ is the abbreviation used for the cosecant of angle $A$.

Ans: The given statement is false because $\cos A$ is the abbreviation used for the cosine of angle $A$. Abbreviation used for the cosecant of angle $A$ is $\operatorname{cosec}A$.

(iv) $\cot A$ is the product of $\cot $ and $A$.

Ans: $\cot A$ is the abbreviation used for the cotangent of angle $A$. Hence the given statement is false.

(v) For some angle $\theta $, $\sin \theta =\dfrac{4}{3}$.

Ans: We know that in the right triangle $\sin \theta =\dfrac{\text{opposite side}}{\text{hypotenuse}}$ .

We know that in the right triangle the hypotenuse is the largest side.

Therefore, the value of $\sin \theta $ must be less than $1$.

In the given statement $\sin \theta =\dfrac{4}{3}$, which is greater than $1$.

Therefore, the given statement is false.

Exercise 8.2

1. Evaluate the following:

(i) $\sin 60{}^\circ \cos 30{}^\circ +\sin 30{}^\circ \cos 60{}^\circ $ 

Ans: With the help of trigonometric ratio tables we can find the values of standard trigonometric angles. The trigonometric ratio table is as follows:

We have to evaluate $\sin 60{}^\circ \cos 30{}^\circ +\sin 30{}^\circ \cos 60{}^\circ $.

Substitute the values from the above table, we get

$\Rightarrow \dfrac{\sqrt{3}}{2}\times \dfrac{\sqrt{3}}{2}+\dfrac{1}{2}\times \dfrac{1}{2}$

$\Rightarrow \dfrac{3}{4}+\dfrac{1}{4}$ 

$\Rightarrow \dfrac{4}{4}$ 

$\therefore \sin 60{}^\circ \cos 30{}^\circ +\sin 30{}^\circ \cos 60{}^\circ =1$.

(ii) $2{{\tan }^{2}}45{}^\circ +{{\cos }^{2}}30{}^\circ -{{\sin }^{2}}60{}^\circ $

Ans: With the help of trigonometric ratio tables we can find the values of standard trigonometric angles. The trigonometric ratio table is as follows:

We have to evaluate $2{{\tan }^{2}}45{}^\circ +{{\cos }^{2}}30{}^\circ -{{\sin }^{2}}60{}^\circ $.

Substitute the values from the above table, we get

$\Rightarrow 2{{\left( 1 \right)}^{2}}+{{\left( \dfrac{\sqrt{3}}{2} \right)}^{2}}-{{\left( \dfrac{\sqrt{3}}{2} \right)}^{2}}$

$\Rightarrow 2+\dfrac{3}{4}-\dfrac{3}{4}$ 

$\Rightarrow 2$ 

$\therefore 2{{\tan }^{2}}45{}^\circ +{{\cos }^{2}}30{}^\circ -{{\sin }^{2}}60{}^\circ =2$.

(iii) $\dfrac{\cos 45{}^\circ }{\sec 30{}^\circ +\operatorname{cosec}30{}^\circ }$

Ans: With the help of trigonometric ratio tables we can find the values of standard trigonometric angles. The trigonometric ratio table is as follows:

We have to evaluate $\dfrac{\cos 45{}^\circ }{\sec 30{}^\circ +\operatorname{cosec}30{}^\circ }$.

Substitute the values from the above table, we get

$\Rightarrow \dfrac{\dfrac{1}{\sqrt{2}}}{\dfrac{2}{\sqrt{3}}+2}$

$\Rightarrow \dfrac{\dfrac{1}{\sqrt{2}}}{\dfrac{2+2\sqrt{3}}{\sqrt{3}}}$ 

\[\Rightarrow \dfrac{1}{\sqrt{2}}\times \dfrac{\sqrt{3}}{2+2\sqrt{3}}\]

Multiplying and dividing by \[\sqrt{3}-1\], we get

\[\Rightarrow \dfrac{1}{\sqrt{2}}\times \dfrac{\sqrt{3}}{2+2\sqrt{3}}\times \dfrac{\sqrt{3}-1}{\sqrt{3}-1}\]

\[\Rightarrow \dfrac{\sqrt{3}\left( \sqrt{3}-1 \right)}{\sqrt{2}\left( 2+2\sqrt{3} \right)\left( \sqrt{3}-1 \right)}\]

\[\Rightarrow \dfrac{\sqrt{3}\left( \sqrt{3}-1 \right)}{2\sqrt{2}\left( \sqrt{3}+1 \right)\left( \sqrt{3}-1 \right)}\]

\[\Rightarrow \dfrac{3-\sqrt{3}}{2\sqrt{2}\left( {{\left( \sqrt{3} \right)}^{2}}-{{1}^{2}} \right)}\]

\[\Rightarrow \dfrac{3-\sqrt{3}}{2\sqrt{2}\left( 3-1 \right)}\]

$\Rightarrow \dfrac{3-\sqrt{3}}{4\sqrt{2}}$ 

$\therefore \dfrac{\cos 45{}^\circ }{\sec 30{}^\circ +\operatorname{cosec}30{}^\circ }=\dfrac{3-\sqrt{3}}{4\sqrt{2}}$

(iv) $\dfrac{\sin 30{}^\circ +\tan 45{}^\circ -\operatorname{cosec}60{}^\circ }{\sec 30{}^\circ +\cos 60{}^\circ -\cot 45{}^\circ }$

Ans: With the help of trigonometric ratio tables we can find the values of standard trigonometric angles. The trigonometric ratio table is as follows:

We have to evaluate $\dfrac{\sin 30{}^\circ +\tan 45{}^\circ -\operatorname{cosec}60{}^\circ }{\sec 30{}^\circ +\cos 60{}^\circ -\cot 45{}^\circ }$.

Substitute the values from the above table, we get

$\Rightarrow \dfrac{\dfrac{1}{2}+1-\dfrac{2}{\sqrt{3}}}{\dfrac{2}{\sqrt{3}}+\dfrac{1}{2}+1}$

$\Rightarrow \dfrac{\dfrac{3}{2}-\dfrac{2}{\sqrt{3}}}{\dfrac{2}{\sqrt{3}}+\dfrac{3}{2}}$

$\Rightarrow \dfrac{\dfrac{3\sqrt{3}-4}{2\sqrt{3}}}{\dfrac{3\sqrt{3}+4}{2\sqrt{3}}}$

$\Rightarrow \dfrac{3\sqrt{3}-4}{3\sqrt{3}+4}$

Multiplying and dividing by \[3\sqrt{3}-4\], we get

\[\Rightarrow \dfrac{3\sqrt{3}-4}{3\sqrt{3}+4}\times \dfrac{3\sqrt{3}-4}{3\sqrt{3}-4}\]

Now, applying the identity $\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}$, we get

\[\Rightarrow \dfrac{{{\left( 3\sqrt{3}-4 \right)}^{2}}}{{{\left( 3\sqrt{3} \right)}^{2}}-{{4}^{2}}}\]

\[\Rightarrow \dfrac{{{\left( 3\sqrt{3}-4 \right)}^{2}}}{{{\left( 3\sqrt{3} \right)}^{2}}-{{4}^{2}}}\]

\[\Rightarrow \dfrac{27+16-24\sqrt{3}}{27-16}\]

$\Rightarrow \dfrac{43-24\sqrt{3}}{11}$ 

$\therefore \dfrac{\sin 30{}^\circ +\tan 45{}^\circ -\operatorname{cosec}60{}^\circ }{\sec 30{}^\circ +\cos 60{}^\circ -\cot 45{}^\circ }=\dfrac{43-24\sqrt{3}}{11}$

(v) $\dfrac{5{{\cos }^{2}}60{}^\circ +4{{\sec }^{2}}30{}^\circ -{{\tan }^{2}}45{}^\circ }{{{\sec }^{2}}30{}^\circ +{{\cos }^{2}}30{}^\circ }$

Ans: With the help of trigonometric ratio tables we can find the values of standard trigonometric angles. The trigonometric ratio table is as follows:

We have to evaluate $\dfrac{5{{\cos }^{2}}60{}^\circ +4{{\sec }^{2}}30{}^\circ -{{\tan }^{2}}45{}^\circ }{{{\sec }^{2}}30{}^\circ +{{\cos }^{2}}30{}^\circ }$.

Substitute the values from the above table, we get

$\Rightarrow \dfrac{5{{\left( \dfrac{1}{2} \right)}^{2}}+4{{\left( \dfrac{2}{\sqrt{3}} \right)}^{2}}-{{1}^{2}}}{{{\left( \dfrac{1}{2} \right)}^{2}}+{{\left( \dfrac{\sqrt{3}}{2} \right)}^{2}}}$

$\Rightarrow \dfrac{5\left( \dfrac{1}{4} \right)+4\left( \dfrac{4}{3} \right)-1}{\left( \dfrac{1}{4} \right)+\left( \dfrac{3}{4} \right)}$

$\Rightarrow \dfrac{\dfrac{15+64-12}{12}}{\dfrac{1+3}{4}}$

$\Rightarrow \dfrac{\dfrac{15+64-12}{12}}{\dfrac{1+3}{4}}$

$\Rightarrow \dfrac{\dfrac{15+64-12}{12}}{\dfrac{4}{4}}$ 

$\Rightarrow \dfrac{\dfrac{67}{12}}{1}$ 

$\therefore \dfrac{5{{\cos }^{2}}60{}^\circ +4{{\sec }^{2}}30{}^\circ -{{\tan }^{2}}45{}^\circ }{{{\sec }^{2}}30{}^\circ +{{\cos }^{2}}30{}^\circ }=\dfrac{67}{12}$.

2. Choose the correct option and justify your choice.

(i) $\dfrac{2\tan 30{}^\circ }{1+{{\tan }^{2}}30{}^\circ }=$ ………

(a) $\sin 60{}^\circ $ 

(b) $\cos 60{}^\circ $ 

(c) $\tan 60{}^\circ $ 

(d) $\sin 30{}^\circ $ 

Ans: The given expression is $\dfrac{2\tan 30{}^\circ }{1+{{\tan }^{2}}30{}^\circ }$.

We know that from the trigonometric ratio table we have $\tan 30{}^\circ =\dfrac{1}{\sqrt{3}}$.

Substitute the value in the given expression we get

$\dfrac{2\tan 30{}^\circ }{1+{{\tan }^{2}}30{}^\circ }=\dfrac{2\left( \dfrac{1}{\sqrt{3}} \right)}{1+{{\left( \dfrac{1}{\sqrt{3}} \right)}^{2}}}$

$\Rightarrow \dfrac{2\tan 30{}^\circ }{1+{{\tan }^{2}}30{}^\circ }=\dfrac{\dfrac{2}{\sqrt{3}}}{1+\dfrac{1}{3}}$

$\Rightarrow \dfrac{2\tan 30{}^\circ }{1+{{\tan }^{2}}30{}^\circ }=\dfrac{\dfrac{2}{\sqrt{3}}}{\dfrac{4}{3}}$

$\Rightarrow \dfrac{2\tan 30{}^\circ }{1+{{\tan }^{2}}30{}^\circ }=\dfrac{\sqrt{3}}{2}$

From the trigonometric table we know that 

$\sin 60{}^\circ =\dfrac{\sqrt{3}}{2}$ 

$\cos 60{}^\circ =\dfrac{1}{2}$ 

$\tan 60{}^\circ =\sqrt{3}$ 

$\sin 30{}^\circ =\dfrac{1}{2}$

Hence, $\dfrac{2\tan 30{}^\circ }{1+{{\tan }^{2}}30{}^\circ }=\sin 60{}^\circ $.

Therefore, option (A) is the correct answer.

(ii) $\dfrac{1-{{\tan }^{2}}45{}^\circ }{1+{{\tan }^{2}}45{}^\circ }=$ ………

(a) $\tan 90{}^\circ $ 

(b) $1$ 

(c) $\sin 45{}^\circ $ 

(d) $0$

Ans: The given expression is $\dfrac{1-{{\tan }^{2}}45{}^\circ }{1+{{\tan }^{2}}45{}^\circ }$.

We know that from the trigonometric ratio table we have $\tan 45{}^\circ =1$.

Substitute the value in the given expression we get

$\dfrac{1-{{\tan }^{2}}45{}^\circ }{1+{{\tan }^{2}}45{}^\circ }=\dfrac{1-{{1}^{2}}}{1+{{1}^{2}}}$

$\Rightarrow \dfrac{1-{{\tan }^{2}}45{}^\circ }{1+{{\tan }^{2}}45{}^\circ }=\dfrac{1-1}{1+1}$

$\Rightarrow \Rightarrow \dfrac{1-{{\tan }^{2}}45{}^\circ }{1+{{\tan }^{2}}45{}^\circ }=\dfrac{0}{2}$

$\therefore \dfrac{1-{{\tan }^{2}}45{}^\circ }{1+{{\tan }^{2}}45{}^\circ }=0$

Therefore, option (D) is the correct answer.

(iii) $\sin 2A=2\sin A$ is true when $A=$ ……..

(a) $0{}^\circ $ 

(b) $30{}^\circ $ 

(c) $45{}^\circ $ 

(d) $60{}^\circ $ 

Ans: The given expression is $\sin 2A=2\sin A$.

We know that from the trigonometric ratio table we have 

$\sin 0{}^\circ =0$

$\sin 30{}^\circ =\dfrac{1}{2}$

$\sin 45{}^\circ =\dfrac{1}{\sqrt{2}}$

$\sin 60{}^\circ =\dfrac{\sqrt{3}}{2}$  

$\sin 90{}^\circ =1$ 

The given statement is true when $A=0{}^\circ $.

Substitute the value in the given expression we get

$\Rightarrow \sin 2A=2\sin A$

$\Rightarrow \sin 2\times 0{}^\circ =2\sin 0{}^\circ $

$0=0$ 

Therefore, option (A) is the correct answer.

(iv) $\dfrac{2\tan 30{}^\circ }{1-{{\tan }^{2}}30{}^\circ }=$………

(a) $\sin 60{}^\circ $ 

(b) $\cos 60{}^\circ $ 

(c) $\tan 60{}^\circ $ 

(d) $\sin 30{}^\circ $ 

Ans: The given expression is $\dfrac{2\tan 30{}^\circ }{1-{{\tan }^{2}}30{}^\circ }$.

We know that from the trigonometric ratio table we have $\tan 30{}^\circ =\dfrac{1}{\sqrt{3}}$.

Substitute the value in the given expression we get

$\dfrac{2\tan 30{}^\circ }{1-{{\tan }^{2}}30{}^\circ }=\dfrac{2\left( \dfrac{1}{\sqrt{3}} \right)}{1-{{\left( \dfrac{1}{\sqrt{3}} \right)}^{2}}}$

$\Rightarrow \dfrac{2\tan 30{}^\circ }{1-{{\tan }^{2}}30{}^\circ }=\dfrac{\dfrac{2}{\sqrt{3}}}{1-\dfrac{1}{3}}$

$\Rightarrow \dfrac{2\tan 30{}^\circ }{1-{{\tan }^{2}}30{}^\circ }=\dfrac{\dfrac{2}{\sqrt{3}}}{\dfrac{2}{3}}$

$\Rightarrow \dfrac{2\tan 30{}^\circ }{1-{{\tan }^{2}}30{}^\circ }=\sqrt{3}$

From the trigonometric table we know that 

$\sin 60{}^\circ =\dfrac{\sqrt{3}}{2}$ 

$\cos 60{}^\circ =\dfrac{1}{2}$ 

$\tan 60{}^\circ =\sqrt{3}$ 

$\sin 30{}^\circ =\dfrac{1}{2}$

Hence, $\dfrac{2\tan 30{}^\circ }{1-{{\tan }^{2}}30{}^\circ }=\tan 60{}^\circ $.

Therefore, option (C) is the correct answer.

3. If $\tan \left( A+B \right)=\sqrt{3}$ and $\tan \left( A-B \right)=\dfrac{1}{\sqrt{3}}$, $0{}^\circ <A+B\le 90{}^\circ $. Find $A$ and $B$.

Ans: Given that $\tan \left( A+ dB \right)=\sqrt{3}$ and $\tan \left( A-B \right)=\dfrac{1}{\sqrt{3}}$.

From the trigonometric ratio table we know that $\tan 60{}^\circ =\sqrt{3}$ and $\tan 30{}^\circ =\dfrac{1}{\sqrt{3}}$.

Then we get

$\tan \left( A+B \right)=\sqrt{3}$

$\Rightarrow \tan \left( A+B \right)=\tan 60{}^\circ $

$\Rightarrow A+B=60{}^\circ $ ……….(1)

Also, $\tan \left( A-B \right)=\dfrac{1}{\sqrt{3}}$

$\Rightarrow \tan \left( A-B \right)=\tan 30{}^\circ $

$\Rightarrow A-B=30{}^\circ $ ……….(2)

Adding eq. (1) and (2), we get

$2A=90{}^\circ $

$\therefore A=45{}^\circ $ 

Substitute the obtained value in eq. (1), we get

$45{}^\circ +B=60{}^\circ $ 

$\Rightarrow B=60{}^\circ -45{}^\circ $ 

$\therefore B=15{}^\circ $ 

Therefore, the values of $A$ and $B$ is $45{}^\circ $ and $15{}^\circ $ respectively.

4. State whether the following are true or false. Justify your answer.

(i) $\sin \left( A+B \right)=\sin A+\sin B$.

Ans: Let us assume $A=30{}^\circ $ and $B=60{}^\circ $.

Now, let us consider LHS of the given expression, we get

$\sin \left( A+B \right)$

Substitute the assumed values in the LHS, we get

$\sin \left( A+B \right)=\sin \left( 30{}^\circ +60{}^\circ  \right)$

$\Rightarrow \sin \left( A+B \right)=\sin \left( 90{}^\circ  \right)$ 

From the trigonometric ratio table we know that $\sin 90{}^\circ =1$, we get

$\Rightarrow \sin \left( A+B \right)=1$

Now, let us consider the RHS of the given expression and substitute the values, we get

$\sin A+\sin B=\sin 30{}^\circ +\sin 60{}^\circ $

From the trigonometric ratio table we know that $\sin 30{}^\circ =\dfrac{1}{2}$ and $\sin 60{}^\circ =\dfrac{\sqrt{3}}{2}$, we get

$\Rightarrow \sin A+\sin B=\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}$

$\Rightarrow \sin A+\sin B=\dfrac{1+\sqrt{3}}{2}$

Thus, $LHS\ne RHS$.

Therefore, the given statement is false.

(ii) The value of $\sin \theta $ increases as $\theta $ increases. 

Ans: The value of sine from the trigonometric ratio table is as follows:

$\sin 0{}^\circ =0$

$\sin 30{}^\circ =\dfrac{1}{2}=0.5$

$\sin 45{}^\circ =\dfrac{1}{\sqrt{2}}=0.707$

$\sin 60{}^\circ =\dfrac{\sqrt{3}}{2}=0.866$  

$\sin 90{}^\circ =1$ 

Therefore, we can conclude that the value of $\sin \theta $ increases as $\theta $ increases. 

Therefore, the given statement is true.

(iii) The value of $\cos \theta $ increases as $\theta $ increases. 

Ans: The value of cosine from the trigonometric ratio table is as follows:

$\cos 0{}^\circ =1$

$\cos 30{}^\circ =\dfrac{\sqrt{3}}{2}=0.866$

$\cos 45{}^\circ =\dfrac{1}{\sqrt{2}}=0.707$

$\cos 60{}^\circ =\dfrac{1}{2}=0.5$  

$\cos 90{}^\circ =0$ 

Therefore, we can conclude that the value of $\cos \theta $ decreases as $\theta $ increases. 

Therefore, the given statement is false.

(iv) \[\sin \theta =\cos \theta \] for all values of \[\theta \].

Ans: The trigonometric ratio table is given as follows:

From the above table we can conclude that \[\sin \theta =\cos \theta \] is true only for $\theta =45{}^\circ $.

\[\sin \theta =\cos \theta \] is not true for all values of $\theta $.

Therefore, the given statement is false.

(v) $\cot A$ is not defined for $A=0{}^\circ $.

Ans: We know that $\cot A=\dfrac{\cos A}{\sin A}$ .

If $A=0{}^\circ $, then $\cot 0{}^\circ =\dfrac{\cos 0{}^\circ }{\sin 0{}^\circ }$

From trigonometric ratio table we get

$\sin 0{}^\circ =0$ and $\cos 0{}^\circ =1$

We get

$\cot 0{}^\circ =\dfrac{1}{0}$, which is undefined.

Therefore, the given statement is true.

Exercise 8.3

1. Express the trigonometric ratios $\sin A,\sec A$ and $\tan A$ in terms of $\cot A$.

Ans: For a right triangle we have an identity ${{\operatorname{cosec}}^{2}}A=1+{{\cot }^{2}}A$.

Let us consider the above identity, we get

${{\operatorname{cosec}}^{2}}A=1+{{\cot }^{2}}A$

Now, reciprocating both sides we get

$\Rightarrow \dfrac{1}{{{\operatorname{cosec}}^{2}}A}=\dfrac{1}{1+{{\cot }^{2}}A}$

Now, we know that $\dfrac{1}{{{\operatorname{cosec}}^{2}}A}={{\sin }^{2}}A$, we get

$\Rightarrow {{\sin }^{2}}A=\dfrac{1}{1+{{\cot }^{2}}A}$

$\Rightarrow \sin A=\pm \dfrac{1}{\sqrt{1+{{\cot }^{2}}A}}$

Now, we know that sine value will be negative for angles greater than $180{}^\circ $, for a triangle sine value is always positive with respect to an angle. Then we will consider only positive values.

$\therefore \sin A=\dfrac{1}{\sqrt{1+{{\cot }^{2}}A}}$ 

We know that $\tan A=\dfrac{1}{\cot A}$ 

Also, we will use the identity ${{\sec }^{2}}A=1+{{\tan }^{2}}A$, we get

${{\sec }^{2}}A=1+{{\tan }^{2}}A$

$\Rightarrow {{\sec }^{2}}A=1+\dfrac{1}{{{\cot }^{2}}A}$

$\Rightarrow {{\sec }^{2}}A=\dfrac{{{\cot }^{2}}A+1}{{{\cot }^{2}}A}$

\[\Rightarrow \sec A=\dfrac{\sqrt{{{\cot }^{2}}A+1}}{\sqrt{{{\cot }^{2}}A}}\]

\[\therefore \sec A=\dfrac{\sqrt{{{\cot }^{2}}A+1}}{\cot A}\]

2. Write all the other trigonometric ratios of $\angle A$ in terms of $\sec A$.

Ans: 

We know that $\cos A=\dfrac{1}{\sec A}$.

$\therefore \cos A=\dfrac{1}{\sec A}$

For a right triangle we have an identity ${{\sin }^{2}}A+{{\cos }^{2}}A=1$.

Let us consider the above identity, we get

${{\sin }^{2}}A+{{\cos }^{2}}A=1$

Now, we know that $\cos A=\dfrac{1}{\sec A}$, we get

$\Rightarrow {{\sin }^{2}}A=1-{{\cos }^{2}}A$

$\Rightarrow {{\sin }^{2}}A=1-\dfrac{1}{{{\sec }^{2}}A}$

$\Rightarrow \sin A=\sqrt{1-{{\left( \dfrac{1}{\sec A} \right)}^{2}}}$

$\therefore \sin A=\dfrac{\sqrt{{{\sec }^{2}}A-1}}{\sec A}$

Also, we will use the identity ${{\sec }^{2}}A=1+{{\tan }^{2}}A$, we get

${{\tan }^{2}}A={{\sec }^{2}}A-1$

$\therefore \tan A=\sqrt{{{\sec }^{2}}A-1}$ 

Now, we know that $\cot A=\dfrac{\cos A}{\sin A}$, we get

$\Rightarrow \cot A=\dfrac{\dfrac{1}{\sec A}}{\dfrac{\sqrt{{{\sec }^{2}}A-1}}{\sec A}}$

$\therefore \cot A=\dfrac{1}{\sqrt{{{\sec }^{2}}A-1}}$

We know that $cosecA=\dfrac{1}{\sin A}$, we get

 $\therefore cosecA=\dfrac{\sec A}{\sqrt{{{\sec }^{2}}A-1}}$

3. Evaluate the following:

(i) $\dfrac{{{\sin }^{2}}63{}^\circ +{{\sin }^{2}}27{}^\circ }{{{\cos }^{2}}17{}^\circ +{{\cos }^{2}}73{}^\circ }$ 

Ans: The given expression is $\dfrac{{{\sin }^{2}}63{}^\circ +{{\sin }^{2}}27{}^\circ }{{{\cos }^{2}}17{}^\circ +{{\cos }^{2}}73{}^\circ }$.

The above expression can be written as 

$\dfrac{{{\sin }^{2}}63{}^\circ +{{\sin }^{2}}27{}^\circ }{{{\cos }^{2}}17{}^\circ +{{\cos }^{2}}73{}^\circ }=\dfrac{{{\left[ \sin \left( 90{}^\circ -27{}^\circ  \right) \right]}^{2}}+{{\sin }^{2}}27{}^\circ }{{{\left[ \cos \left( 90{}^\circ -73{}^\circ  \right) \right]}^{2}}+{{\cos }^{2}}73{}^\circ }$

Now, we can apply the identity $\cos \left( 90{}^\circ -\theta  \right)=\sin \theta $ and $\sin \left( 90{}^\circ -\theta  \right)=\cos \theta $, we get

$\Rightarrow \dfrac{{{\sin }^{2}}63{}^\circ +{{\sin }^{2}}27{}^\circ }{{{\cos }^{2}}17{}^\circ +{{\cos }^{2}}73{}^\circ }=\dfrac{{{\cos }^{2}}27{}^\circ +{{\sin }^{2}}27{}^\circ }{{{\sin }^{2}}73{}^\circ +{{\cos }^{2}}73{}^\circ }$

Now, by applying the trigonometric identity ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$, we get

$\Rightarrow \dfrac{{{\sin }^{2}}63{}^\circ +{{\sin }^{2}}27{}^\circ }{{{\cos }^{2}}17{}^\circ +{{\cos }^{2}}73{}^\circ }=\dfrac{1}{1}$ 

$\therefore \dfrac{{{\sin }^{2}}63{}^\circ +{{\sin }^{2}}27{}^\circ }{{{\cos }^{2}}17{}^\circ +{{\cos }^{2}}73{}^\circ }=1$

(ii) $\sin 25{}^\circ \cos 65{}^\circ +\cos 25{}^\circ \sin 65{}^\circ $ 

Ans: The given expression is $\sin 25{}^\circ \cos 65{}^\circ +\cos 25{}^\circ \sin 65{}^\circ $ .

The above expression can be written as 

$\sin 25{}^\circ \cos 65{}^\circ +\cos 25{}^\circ \sin 65{}^\circ =\sin 25{}^\circ \cos \left( 90{}^\circ -25{}^\circ  \right)+\cos 25{}^\circ \sin \left( 90{}^\circ -25{}^\circ  \right)$

Now, we can apply the identity $\cos \left( 90{}^\circ -\theta  \right)=\sin \theta $ and $\sin \left( 90{}^\circ -\theta  \right)=\cos \theta $, we get

\[\Rightarrow \sin 25{}^\circ \cos 65{}^\circ +\cos 25{}^\circ \sin 65{}^\circ =\sin 25{}^\circ \sin 25{}^\circ +\cos 25{}^\circ \cos 25{}^\circ \]

\[\Rightarrow \sin 25{}^\circ \cos 65{}^\circ +\cos 25{}^\circ \sin 65{}^\circ ={{\sin }^{2}}25{}^\circ +{{\cos }^{2}}25{}^\circ \]

Now, by applying the trigonometric identity ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$, we get

\[\Rightarrow \sin 25{}^\circ \cos 65{}^\circ +\cos 25{}^\circ \sin 65{}^\circ =1\] 

\[\therefore \sin 25{}^\circ \cos 65{}^\circ +\cos 25{}^\circ \sin 65{}^\circ =1\]

4. Choose the correct option and justify your choice:

(i) \[9{{\sec }^{2}}A-9{{\tan }^{2}}A=\] …….

(a) $1$ 

(b) $9$

(c) $8$ 

(d) $0$

Ans: The given expression is $9{{\sec }^{2}}A-9{{\tan }^{2}}A$.

The given expression can be written as 

$\Rightarrow 9{{\sec }^{2}}A-9{{\tan }^{2}}A=9\left( {{\sec }^{2}}A-{{\tan }^{2}}A \right)$

Now, we will use the identity ${{\sec }^{2}}A=1+{{\tan }^{2}}A$, we get

${{\sec }^{2}}A-{{\tan }^{2}}A=1$

$\Rightarrow 9{{\sec }^{2}}A-9{{\tan }^{2}}A=9\left( 1 \right)$

$\therefore 9{{\sec }^{2}}A-9{{\tan }^{2}}A=9$

Therefore, option (B) is the correct answer.

(ii) $\left( 1+\tan \theta +\sec \theta  \right)\left( 1+\cot \theta -\operatorname{cosec}\theta  \right)$ 

(a) $0$

(b) $1$

(c) $2$

(d) $-1$

Ans: The given expression is $\left( 1+\tan \theta +\sec \theta  \right)\left( 1+\cot \theta -\operatorname{cosec}\theta  \right)$.

We know that the trigonometric functions have values as:

$\tan \theta =\dfrac{\sin \theta }{\cos \theta }$, $\cot \theta =\dfrac{\cos \theta }{\sin \theta }=\dfrac{1}{\tan \theta }$, $cosec\theta =\dfrac{1}{\sin \theta }$ and $sec\theta =\dfrac{1}{\cos \theta }$

Substituting these values in the given expression, we get

$\Rightarrow \left( 1+\tan \theta +\sec \theta  \right)\left( 1+\cot \theta -\operatorname{cosec}\theta  \right)=\left( 1+\dfrac{\sin \theta }{\cos \theta }+\dfrac{1}{\cos \theta } \right)\left( 1+\dfrac{\cos \theta }{\sin \theta }-\dfrac{1}{\sin \theta } \right)$

$\Rightarrow \left( 1+\tan \theta +\sec \theta  \right)\left( 1+\cot \theta -\operatorname{cosec}\theta  \right)=\left( \dfrac{\cos \theta +\sin \theta +1}{\cos \theta } \right)\left( \dfrac{\sin \theta +\cos \theta -1}{\sin \theta } \right)$

Now, by applying the identity $\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}$, we get

$\Rightarrow \left( 1+\tan \theta +\sec \theta  \right)\left( 1+\cot \theta -\operatorname{cosec}\theta  \right)=\dfrac{{{\left( \sin \theta +\cos \theta  \right)}^{2}}-{{1}^{2}}}{\sin \theta \cos \theta }$

$\Rightarrow \left( 1+\tan \theta +\sec \theta  \right)\left( 1+\cot \theta -\operatorname{cosec}\theta  \right)=\dfrac{{{\sin }^{2}}\theta +{{\cos }^{2}}\theta +2\sin \theta \cos \theta -1}{\sin \theta \cos \theta }$

Now, by applying the trigonometric identity ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$, we get

$\Rightarrow \left( 1+\tan \theta +\sec \theta  \right)\left( 1+\cot \theta -\operatorname{cosec}\theta  \right)=\dfrac{1+2\sin \theta \cos \theta -1}{\sin \theta \cos \theta }$

$\Rightarrow \left( 1+\tan \theta +\sec \theta  \right)\left( 1+\cot \theta -\operatorname{cosec}\theta  \right)=\dfrac{2\sin \theta \cos \theta }{\sin \theta \cos \theta }$

$\therefore \left( 1+\tan \theta +\sec \theta  \right)\left( 1+\cot \theta -\operatorname{cosec}\theta  \right)=2$

Therefore, option (C) is the correct answer.

(iii) $\left( \sec A+\tan A \right)\left( 1-\sin A \right)=$ ………

(a) $\sec A$ 

(b) $\sin A$ 

(c) $cosecA$ 

(d) $\cos A$ 

Ans: Given expression is $\left( \sec A+\tan A \right)\left( 1-\sin A \right)$.

We know that $\tan \theta =\dfrac{\sin \theta }{\cos \theta }$ and $sec\theta =\dfrac{1}{\cos \theta }$

Substituting these values in the given expression, we get

$\left( \sec A+\tan A \right)\left( 1-\sin A \right)=\left( \dfrac{1}{\cos A}+\dfrac{\sin A}{\cos A} \right)\left( 1-\sin A \right)$

$\Rightarrow \left( \sec A+\tan A \right)\left( 1-\sin A \right)=\left( \dfrac{1+\sin A}{\cos A} \right)\left( 1-\sin A \right)$

$\Rightarrow \left( \sec A+\tan A \right)\left( 1-\sin A \right)=\left( \dfrac{\left( 1+\sin A \right)\left( 1-\sin A \right)}{\cos A} \right)$

Now, by applying the identity $\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}$, we get

$\Rightarrow \left( \sec A+\tan A \right)\left( 1-\sin A \right)=\left( \dfrac{{{1}^{2}}-{{\sin }^{2}}A}{\cos A} \right)$

Now, we know that ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$, we get

$\Rightarrow \left( \sec A+\tan A \right)\left( 1-\sin A \right)=\left( \dfrac{{{\cos }^{2}}A}{\cos A} \right)$

$\therefore \left( \sec A+\tan A \right)\left( 1-\sin A \right)=\cos A$

Therefore, option (D) is the correct answer.

(iv) $\dfrac{1+{{\tan }^{2}}A}{1+{{\cot }^{2}}A}$ 

(a) ${{\sec }^{2}}A$ 

(b) $-1$ 

(c) ${{\cot }^{2}}A$ 

(d) ${{\tan }^{2}}A$ 

Ans: Given expression is $\dfrac{1+{{\tan }^{2}}A}{1+{{\cot }^{2}}A}$.

We know that the trigonometric functions have values as:

$\tan \theta =\dfrac{\sin \theta }{\cos \theta }$ and $\cot \theta =\dfrac{\cos \theta }{\sin \theta }=\dfrac{1}{\tan \theta }$.

Substituting these values in the given expression, we get

$\dfrac{1+{{\tan }^{2}}A}{1+{{\cot }^{2}}A}=\dfrac{1+\dfrac{{{\sin }^{2}}A}{{{\cos }^{2}}A}}{1+\dfrac{{{\cos }^{2}}A}{{{\sin }^{2}}A}}$

$\Rightarrow \dfrac{1+{{\tan }^{2}}A}{1+{{\cot }^{2}}A}=\dfrac{\dfrac{{{\cos }^{2}}A+{{\sin }^{2}}A}{{{\cos }^{2}}A}}{\dfrac{{{\sin }^{2}}A+{{\cos }^{2}}A}{{{\sin }^{2}}A}}$

Now, we know that ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$, we get

$\Rightarrow \dfrac{1+{{\tan }^{2}}A}{1+{{\cot }^{2}}A}=\dfrac{\dfrac{1}{{{\cos }^{2}}A}}{\dfrac{1}{{{\sin }^{2}}A}}$

$\Rightarrow \dfrac{1+{{\tan }^{2}}A}{1+{{\cot }^{2}}A}=\dfrac{{{\sin }^{2}}A}{{{\cos }^{2}}A}$

$\Rightarrow \dfrac{1+{{\tan }^{2}}A}{1+{{\cot }^{2}}A}={{\tan }^{2}}A$

Therefore, option (D) is the correct answer.

5. Prove the following identities, where the angles involved are acute angles for which the expressions are defined.

(i) ${{\left( cosec\theta -cot\theta  \right)}^{2}}=\dfrac{1-\cos \theta }{1+\cos \theta }$ 

Ans: Given expression is ${{\left( cosec\theta -\cot \theta  \right)}^{2}}=\dfrac{1-\cos \theta }{1+\cos \theta }$.

Let us consider the LHS of the given expression, we get

$LHS={{\left( cosec\theta -\cot \theta  \right)}^{2}}$

Now, we know that $\cot \theta =\dfrac{\cos \theta }{\sin \theta }=\dfrac{1}{\tan \theta }$ and $cosec\theta =\dfrac{1}{\sin \theta }$.

By substituting the values, we get

$\Rightarrow {{\left( cosec\theta -\cot \theta  \right)}^{2}}={{\left( \dfrac{1}{\sin \theta }-\dfrac{\cos \theta }{\sin \theta } \right)}^{2}}$

 $\Rightarrow {{\left( cosec\theta -\cot \theta  \right)}^{2}}={{\left( \dfrac{1-\cos \theta }{\sin \theta } \right)}^{2}}$

$\Rightarrow {{\left( cosec\theta -\cot \theta  \right)}^{2}}=\dfrac{{{\left( 1-\cos \theta  \right)}^{2}}}{{{\sin }^{2}}\theta }$

Now, we know that ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$, we get

$\Rightarrow {{\left( cosec\theta -\cot \theta  \right)}^{2}}=\dfrac{{{\left( 1-\cos \theta  \right)}^{2}}}{1-{{\cos }^{2}}\theta }$

Now, by applying the identity $\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}$, we get

$\Rightarrow {{\left( cosec\theta -\cot \theta  \right)}^{2}}=\dfrac{{{\left( 1-\cos \theta  \right)}^{2}}}{\left( 1-\cos \theta  \right)\left( 1+\cos \theta  \right)}$

$\Rightarrow {{\left( cosec\theta -\cot \theta  \right)}^{2}}=\dfrac{\left( 1-\cos \theta  \right)}{\left( 1+\cos \theta  \right)}$

$\Rightarrow {{\left( cosec\theta -\cot \theta  \right)}^{2}}=RHS$

$\therefore {{\left( cosec\theta -\cot \theta  \right)}^{2}}=\dfrac{1-\cos \theta }{1+\cos \theta }$

Hence proved

(ii) $\dfrac{\cos A}{1+\sin A}+\dfrac{1+\sin A}{\cos A}=2\sec A$

Ans: Given expression is $\dfrac{\cos A}{1+\sin A}+\dfrac{1+\sin A}{\cos A}=2\sec A$.

Let us consider the LHS of the given expression, we get

$LHS=\dfrac{\cos A}{1+\sin A}+\dfrac{1+\sin A}{\cos A}$

Now, taking LCM, we get

$\Rightarrow \dfrac{\cos A}{1+\sin A}+\dfrac{1+\sin A}{\cos A}=\dfrac{{{\cos }^{2}}A+\left( 1+\sin A \right)\left( 1+\sin A \right)}{\left( 1+\sin A \right)\cos A}$

$\Rightarrow \dfrac{\cos A}{1+\sin A}+\dfrac{1+\sin A}{\cos A}=\dfrac{{{\cos }^{2}}A+{{\sin }^{2}}A+2\sin A+1}{\left( 1+\sin A \right)\cos A}$

Now, we know that ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$, we get

$\Rightarrow \dfrac{\cos A}{1+\sin A}+\dfrac{1+\sin A}{\cos A}=\dfrac{1+2\sin A+1}{\left( 1+\sin A \right)\cos A}$

$\Rightarrow \dfrac{\cos A}{1+\sin A}+\dfrac{1+\sin A}{\cos A}=\dfrac{2+2\sin A}{\left( 1+\sin A \right)\cos A}$

$\Rightarrow \dfrac{\cos A}{1+\sin A}+\dfrac{1+\sin A}{\cos A}=\dfrac{2\left( 1+\sin A \right)}{\left( 1+\sin A \right)\cos A}$

$\Rightarrow \dfrac{\cos A}{1+\sin A}+\dfrac{1+\sin A}{\cos A}=\dfrac{2}{\cos A}$

We know that $sec\theta =\dfrac{1}{\cos \theta }$, we get

$\Rightarrow \dfrac{\cos A}{1+\sin A}+\dfrac{1+\sin A}{\cos A}=2\sec A$

\[\Rightarrow \dfrac{\cos A}{1+\sin A}+\dfrac{1+\sin A}{\cos A}=RHS\]

\[\therefore \dfrac{\cos A}{1+\sin A}+\dfrac{1+\sin A}{\cos A}=2\sec A\]

Hence proved

(iii) $\dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }=1+\sec \theta cosec\theta $ 

Ans: Given expression is $\dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }=1+\sec \theta \operatorname{cosec}\theta $.

Let us consider the LHS of the given expression, we get

$LHS=\dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }$

Now, we know that $\tan \theta =\dfrac{\sin \theta }{\cos \theta }$ and $\cot \theta =\dfrac{\cos \theta }{\sin \theta }=\dfrac{1}{\tan \theta }$.

By substituting the values, we get

\[\Rightarrow \dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }=\left( \dfrac{\dfrac{\sin \theta }{\cos \theta }}{1-\dfrac{\cos \theta }{\sin \theta }}+\dfrac{\dfrac{\cos \theta }{\sin \theta }}{1-\dfrac{\sin \theta }{\cos \theta }} \right)\]

\[\Rightarrow \dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }=\left( \dfrac{\dfrac{\sin \theta }{\cos \theta }}{\dfrac{\sin \theta -\cos \theta }{\sin \theta }}+\dfrac{\dfrac{\cos \theta }{\sin \theta }}{\dfrac{\cos \theta -\sin \theta }{\cos \theta }} \right)\]

 \[\Rightarrow \dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }=\left( \dfrac{{{\sin }^{2}}\theta }{\cos \theta \left( \sin \theta -\cos \theta  \right)}+\dfrac{{{\cos }^{2}}\theta }{\sin \theta \left( \sin \theta -\cos \theta  \right)} \right)\]

\[\Rightarrow \dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }=\dfrac{1}{\left( \sin \theta -\cos \theta  \right)}\left( \dfrac{{{\sin }^{2}}\theta }{\cos \theta }+\dfrac{{{\cos }^{2}}\theta }{\sin \theta } \right)\]

\[\Rightarrow \dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }=\dfrac{1}{\left( \sin \theta -\cos \theta  \right)}\left( \dfrac{{{\sin }^{3}}\theta -{{\cos }^{3}}\theta }{\sin \theta \cos \theta } \right)\]

Now, by applying the identity \[{{a}^{3}}-{{b}^{3}}=\left( a-b \right)\left( {{a}^{2}}+ab+{{b}^{2}} \right)\], we get

\[\Rightarrow \dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }=\dfrac{1}{\left( \sin \theta -\cos \theta  \right)}\left[ \dfrac{\left( \sin \theta -\cos \theta  \right)\left( {{\sin }^{2}}\theta +{{\cos }^{2}}\theta +\sin \theta \cos \theta  \right)}{\sin \theta \cos \theta } \right]\]

Now, we know that ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$, we get

\[\Rightarrow \dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }=\dfrac{1}{\left( \sin \theta -\cos \theta  \right)}\left[ \dfrac{\left( \sin \theta -\cos \theta  \right)\left( 1+\sin \theta \cos \theta  \right)}{\sin \theta \cos \theta } \right]\]

\[\Rightarrow \dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }=\dfrac{\left( 1+\sin \theta \cos \theta  \right)}{\sin \theta \cos \theta }\]

\[\Rightarrow \dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }=\dfrac{1}{\sin \theta \cos \theta }+\dfrac{\sin \theta \cos \theta }{\sin \theta \cos \theta }\]

\[\Rightarrow \dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }=\dfrac{1}{\sin \theta \cos \theta }+1\]

We know that $cosec\theta =\dfrac{1}{\sin \theta }$ and $sec\theta =\dfrac{1}{\cos \theta }$, we get

\[\Rightarrow \dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }=\sec \theta cosec\theta +1\]

\[\Rightarrow \dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }=1+\sec \theta cosec\theta \]

\[\Rightarrow \dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }=RHS\]

\[\therefore \dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }=1+\sec \theta cosec\theta \]

Hence proved

(iv) $\dfrac{1+\sec A}{\sec A}=\dfrac{{{\sin }^{2}}A}{1-\cos A}$ 

Ans: Given expression is $\dfrac{1+\sec A}{\sec A}=\dfrac{{{\sin }^{2}}A}{1-\cos A}$.

Let us consider the LHS of the given expression, we get

$LHS=\dfrac{1+\sec A}{\sec A}$

Now, we know that $\sec \theta =\dfrac{1}{\cos \theta }$.

By substituting the value, we get

\[\Rightarrow \dfrac{1+\sec A}{\sec A}=\dfrac{1+\dfrac{1}{\cos A}}{\dfrac{1}{\cos A}}\]

\[\Rightarrow \dfrac{1+\sec A}{\sec A}=\dfrac{\dfrac{\cos A+1}{\cos A}}{\dfrac{1}{\cos A}}\]

 \[\Rightarrow \dfrac{1+\sec A}{\sec A}=\cos A+1\]

Multiply and divide by $\left( 1-\cos A \right)$, we get

 \[\Rightarrow \dfrac{1+\sec A}{\sec A}=\dfrac{\left( 1+\cos A \right)\left( 1-\cos A \right)}{\left( 1-\cos A \right)}\]

Now, by applying the identity $\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}$, we get

\[\Rightarrow \dfrac{1+\sec A}{\sec A}=\dfrac{1-{{\cos }^{2}}A}{\left( 1-\cos A \right)}\]

Now, we know that ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$, we get

\[\Rightarrow \dfrac{1+\sec A}{\sec A}=\dfrac{{{\sin }^{2}}A}{\left( 1-\cos A \right)}\]

\[\Rightarrow \dfrac{1+\sec A}{\sec A}=RHS\]

\[\therefore \dfrac{1+\sec A}{\sec A}=\dfrac{{{\sin }^{2}}A}{1-\cos A}\]

Hence proved

(v) $\dfrac{\cos A-\sin A+1}{\cos A+\sin A-1}=cosecA+\cot A$ 

Ans: Given expression is $\dfrac{\cos A-\sin A+1}{\cos A+\sin A-1}=cosecA+\cot A$.

Now, let us consider the LHS of the given expression, we get

$LHS=\dfrac{\cos A-\sin A+1}{\cos A+\sin A-1}$

Dividing numerator and denominator by $\sin A$, we get

$\Rightarrow \dfrac{\cos A-\sin A+1}{\cos A+\sin A-1}=\dfrac{\dfrac{\cos A}{\sin A}-\dfrac{\sin A}{\sin A}+\dfrac{1}{\sin A}}{\dfrac{\cos A}{\sin A}+\dfrac{\sin A}{\sin A}-\dfrac{1}{\sin A}}$

Now, we know that $\cot \theta =\dfrac{\cos \theta }{\sin \theta }=\dfrac{1}{\tan \theta }$ and $cosec\theta =\dfrac{1}{\sin \theta }$, we get

$\Rightarrow \dfrac{\cos A-\sin A+1}{\cos A+\sin A-1}=\dfrac{\cot A-1+\operatorname{cosec}A}{\cot A+1-\operatorname{cosec}A}$

Now, by applying the identity ${{\operatorname{cosec}}^{2}}A=1+{{\cot }^{2}}A$, substitute $1={{\cot }^{2}}A-{{\operatorname{cosec}}^{2}}A$, we get

$\Rightarrow \dfrac{\cos A-\sin A+1}{\cos A+\sin A-1}=\dfrac{\cot A-\left( {{\cot }^{2}}A-{{\operatorname{cosec}}^{2}}A \right)+\operatorname{cosec}A}{\cot A+{{\cot }^{2}}A-{{\operatorname{cosec}}^{2}}A-\operatorname{cosec}A}$

$\Rightarrow \dfrac{\cos A-\sin A+1}{\cos A+\sin A-1}=\dfrac{\cot A-{{\cot }^{2}}A+{{\operatorname{cosec}}^{2}}A+\operatorname{cosec}A}{\cot A+{{\cot }^{2}}A-{{\operatorname{cosec}}^{2}}A-\operatorname{cosec}A}$

$\Rightarrow \dfrac{\cos A-\sin A+1}{\cos A+\sin A-1}=\dfrac{{{\left( \cot A-1+\operatorname{cosec}A \right)}^{2}}}{{{\cot }^{2}}A-1+{{\operatorname{cosec}}^{2}}A+2\operatorname{cosec}A}$

$\Rightarrow \dfrac{\cos A-\sin A+1}{\cos A+\sin A-1}=\dfrac{{{\left( \cot A-1+\operatorname{cosec}A \right)}^{2}}}{{{\cot }^{2}}A-1+{{\operatorname{cosec}}^{2}}A+2\operatorname{cosec}A}$

$\Rightarrow \dfrac{\cos A-\sin A+1}{\cos A+\sin A-1}=\dfrac{2{{\operatorname{cosec}}^{2}}A+2\cot A\operatorname{cosec}A-2\cot A-2\operatorname{cosec}A}{{{\cot }^{2}}A-1+{{\operatorname{cosec}}^{2}}A+2\operatorname{cosec}A}$

$\Rightarrow \dfrac{\cos A-\sin A+1}{\cos A+\sin A-1}=\dfrac{2\operatorname{cosec}A\left( \cot A-\operatorname{cosec}A \right)-2\left( \cot A-\operatorname{cosec}A \right)}{{{\cot }^{2}}A-1+{{\operatorname{cosec}}^{2}}A+2\operatorname{cosec}A}$

$\Rightarrow \dfrac{\cos A-\sin A+1}{\cos A+\sin A-1}=\dfrac{\left( 2\operatorname{cosec}A-2 \right)\left( \cot A-\operatorname{cosec}A \right)}{1-1+2\operatorname{cosec}A}$

$\Rightarrow \dfrac{\cos A-\sin A+1}{\cos A+\sin A-1}=\dfrac{\left( 2\operatorname{cosec}A-2 \right)\left( \cot A-\operatorname{cosec}A \right)}{2\operatorname{cosec}A}$

$\Rightarrow \dfrac{\cos A-\sin A+1}{\cos A+\sin A-1}=\operatorname{cosec}A+\cot A$

$\Rightarrow \dfrac{\cos A-\sin A+1}{\cos A+\sin A-1}=RHS$

$\therefore \dfrac{\cos A-\sin A+1}{\cos A+\sin A-1}=\operatorname{cosec}A+\cot A$ 

Hence proved

(vi) $\sqrt{\dfrac{1+\sin A}{1-\sin A}}=\sec A+\tan A$ 

Ans: Given expression is $\sqrt{\dfrac{1+\sin A}{1-\sin A}}=\sec A+\tan A$.

Let us consider the LHS of the given expression, we get

$LHS=\sqrt{\dfrac{1+\sin A}{1-\sin A}}$

Now, multiply and divide the expression by $\sqrt{1+\sin A}$, we get

$\Rightarrow \sqrt{\dfrac{1+\sin A}{1-\sin A}}=\sqrt{\dfrac{\left( 1+\sin A \right)\left( 1+\sin A \right)}{\left( 1-\sin A \right)\left( 1+\sin A \right)}}$

Now, by applying the identity $\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}$, we get

\[\Rightarrow \sqrt{\dfrac{1+\sin A}{1-\sin A}}=\sqrt{\dfrac{{{\left( 1+\sin A \right)}^{2}}}{1-{{\sin }^{2}}A}}\]

Now, we know that ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$, we get

\[\Rightarrow \sqrt{\dfrac{1+\sin A}{1-\sin A}}=\dfrac{1+\sin A}{\sqrt{{{\cos }^{2}}A}}\]

\[\Rightarrow \sqrt{\dfrac{1+\sin A}{1-\sin A}}=\dfrac{1+\sin A}{\cos A}\]

\[\Rightarrow \sqrt{\dfrac{1+\sin A}{1-\sin A}}=\dfrac{1}{\cos A}+\dfrac{\sin A}{\cos A}\]

\[\Rightarrow \sqrt{\dfrac{1+\sin A}{1-\sin A}}=\sec A+\tan A\]

\[\Rightarrow \sqrt{\dfrac{1+\sin A}{1-\sin A}}=RHS\]

$\therefore \sqrt{\dfrac{1+\sin A}{1-\sin A}}=\sec A+\tan A$ 

Hence proved

(vii) $\dfrac{\sin \theta -2{{\sin }^{3}}\theta }{2\cos \theta -\cos \theta }=\tan \theta $ 

Ans: Given expression is $\dfrac{\sin \theta -2{{\sin }^{3}}\theta }{2\cos \theta -\cos \theta }=\tan \theta $.

Let us consider the LHS of the given expression, we get

$LHS=\dfrac{\sin \theta -2{{\sin }^{3}}\theta }{2\cos \theta -\cos \theta }$

Taking common terms out, we get

$\Rightarrow \dfrac{\sin \theta -2{{\sin }^{3}}\theta }{2\cos \theta -\cos \theta }=\dfrac{\sin \theta \left( 1-2{{\sin }^{2}}\theta  \right)}{\cos \theta \left( 2{{\cos }^{2}}\theta -1 \right)}$

Now, we know that ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$, we get

$\Rightarrow \dfrac{\sin \theta -2{{\sin }^{3}}\theta }{2\cos \theta -\cos \theta }=\dfrac{\sin \theta \left( 1-2{{\sin }^{2}}\theta  \right)}{\cos \theta \left( 2\left( 1-2{{\sin }^{2}}\theta  \right)-1 \right)}$

$\Rightarrow \dfrac{\sin \theta -2{{\sin }^{3}}\theta }{2\cos \theta -\cos \theta }=\dfrac{\sin \theta \left( 1-2{{\sin }^{2}}\theta  \right)}{\cos \theta \left( 2-2{{\sin }^{2}}\theta -1 \right)}$

$\Rightarrow \dfrac{\sin \theta -2{{\sin }^{3}}\theta }{2\cos \theta -\cos \theta }=\dfrac{\sin \theta \left( 1-2{{\sin }^{2}}\theta  \right)}{\cos \theta \left( 1-2{{\sin }^{2}}\theta  \right)}$

$\Rightarrow \dfrac{\sin \theta -2{{\sin }^{3}}\theta }{2\cos \theta -\cos \theta }=\dfrac{\sin \theta }{\cos \theta }$

$\Rightarrow \dfrac{\sin \theta -2{{\sin }^{3}}\theta }{2\cos \theta -\cos \theta }=\tan \theta $

$\Rightarrow \dfrac{\sin \theta -2{{\sin }^{3}}\theta }{2\cos \theta -\cos \theta }=RHS$

$\therefore \dfrac{\sin \theta -2{{\sin }^{3}}\theta }{2\cos \theta -\cos \theta }=\tan \theta $

Hence proved

(viii) ${{\left( \sin A+cosecA \right)}^{2}}+{{\left( \cos A+secA \right)}^{2}}=7+{{\tan }^{2}}A+{{\cot }^{2}}A$ 

Ans: Given expression is ${{\left( \sin A+cosecA \right)}^{2}}+{{\left( \cos A+\sec A \right)}^{2}}=7+{{\tan }^{2}}A+{{\cot }^{2}}A$.

Let us consider the LHS of the given expression, we get

$LHS={{\left( \sin A+cosecA \right)}^{2}}+{{\left( \cos A+\sec A \right)}^{2}}$

Now, by applying the identity \[{{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}\], we get

\[\Rightarrow {{\left( \sin A+cosecA \right)}^{2}}+{{\left( \cos A+\sec A \right)}^{2}}={{\sin }^{2}}A+cosec{{A}^{2}}+2\sin AcosecA+{{\cos }^{2}}A+{{\sec }^{2}}A+2\cos A\sec A\]\[\Rightarrow {{\left( \sin A+cosecA \right)}^{2}}+{{\left( \cos A+\sec A \right)}^{2}}={{\sin }^{2}}A+{{\cos }^{2}}A+cosec{{A}^{2}}+{{\sec }^{2}}A+2\sin AcosecA+2\cos A\sec A\]We know that ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$, $cosec\theta =\dfrac{1}{\sin \theta }$ and $sec\theta =\dfrac{1}{\cos \theta }$, we get

\[\Rightarrow {{\left( \sin A+cosecA \right)}^{2}}+{{\left( \cos A+\sec A \right)}^{2}}=1+cose{{c}^{2}}\theta +{{\sec }^{2}}\theta +2\sin A\dfrac{1}{\sin A}+2\cos A\dfrac{1}{\cos A}\] 

\[\Rightarrow {{\left( \sin A+cosecA \right)}^{2}}+{{\left( \cos A+\sec A \right)}^{2}}=1+\left( 1+{{\cot }^{2}}A+1+{{\tan }^{2}}A \right)+2+2\]

\[\Rightarrow {{\left( \sin A+cosecA \right)}^{2}}+{{\left( \cos A+\sec A \right)}^{2}}=7+{{\tan }^{2}}A+{{\cot }^{2}}A\]

\[\Rightarrow {{\left( \sin A+cosecA \right)}^{2}}+{{\left( \cos A+\sec A \right)}^{2}}=RHS\]

\[\therefore {{\left( \sin A+cosecA \right)}^{2}}+{{\left( \cos A+\sec A \right)}^{2}}=7+{{\tan }^{2}}A+{{\cot }^{2}}A\]

Hence proved

(ix) $\left( cosecA-\sin A \right)\left( \sec A-\cos A \right)=\dfrac{1}{\tan A+\cot A}$

Ans: Given expression is $\left( cosecA-\sin A \right)\left( \sec A-\cos A \right)=\dfrac{1}{\tan A+\cot A}$.

Let us consider the LHS of the given expression, we get

$LHS=\left( cosecA-\sin A \right)\left( \sec A-\cos A \right)$

We know that $cosec\theta =\dfrac{1}{\sin \theta }$ and $sec\theta =\dfrac{1}{\cos \theta }$, we get

$\Rightarrow \left( cosecA-\sin A \right)\left( \sec A-\cos A \right)=\left( \dfrac{1}{\sin A}-\sin A \right)\left( \dfrac{1}{\cos A}-\cos A \right)$

$\Rightarrow \left( cosecA-\sin A \right)\left( \sec A-\cos A \right)=\left( \dfrac{1-{{\sin }^{2}}A}{\sin A} \right)\left( \dfrac{1-{{\cos }^{2}}A}{\cos A} \right)$

Now, we know that ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$, we get

$\Rightarrow \left( cosecA-\sin A \right)\left( \sec A-\cos A \right)=\left( \dfrac{{{\cos }^{2}}A}{\sin A} \right)\left( \dfrac{{{\sin }^{2}}A}{\cos A} \right)$

$\Rightarrow \left( cosecA-\sin A \right)\left( \sec A-\cos A \right)=\sin A\cos A$

Now, consider the RHS of the given expression, we get

$RHS=\dfrac{1}{\tan A+\cot A}$

Now, we know that $\tan \theta =\dfrac{\sin \theta }{\cos \theta }$ and $\cot \theta =\dfrac{\cos \theta }{\sin \theta }=\dfrac{1}{\tan \theta }$.

$\Rightarrow \dfrac{1}{\tan A+\cot A}=\dfrac{1}{\dfrac{\sin A}{\cos A}+\dfrac{\cos A}{\sin A}}$

$\Rightarrow \dfrac{1}{\tan A+\cot A}=\dfrac{1}{\dfrac{{{\sin }^{2}}A+{{\cos }^{2}}A}{\sin A\cos A}}$

$\Rightarrow \dfrac{1}{\tan A+\cot A}=\dfrac{\sin A\cos A}{{{\sin }^{2}}A+{{\cos }^{2}}A}$

Now, we know that ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$, we get

$\Rightarrow \dfrac{1}{\tan A+\cot A}=\sin A\cos A$

Here, we get LHS=RHS

$\therefore \left( cosecA-\sin A \right)\left( \sec A-\cos A \right)=\dfrac{1}{\tan A+\cot A}$ 

Hence proved

(x) $\left( \dfrac{1+{{\tan }^{2}}A}{1+{{\cot }^{2}}A} \right)={{\left( \dfrac{1-\tan A}{1-\cot A} \right)}^{2}}$

Ans: Given expression is $\dfrac{1+{{\tan }^{2}}A}{1+{{\cot }^{2}}A}={{\left( \dfrac{1-\tan A}{1-\cot A} \right)}^{2}}$.

Let us consider the LHS of the given expression, we get

$LHS=\dfrac{1+{{\tan }^{2}}A}{1+{{\cot }^{2}}A}$

By applying the identities ${{\sec }^{2}}A=1+{{\tan }^{2}}A$ and ${{\operatorname{cosec}}^{2}}A=1+{{\cot }^{2}}A$, we get

$\Rightarrow \dfrac{1+{{\tan }^{2}}A}{1+{{\cot }^{2}}A}=\dfrac{se{{c}^{2}}A}{{{\operatorname{cosec}}^{2}}A}$

We know that $cosec\theta =\dfrac{1}{\sin \theta }$ and $sec\theta =\dfrac{1}{\cos \theta }$, we get

$\Rightarrow \dfrac{1+{{\tan }^{2}}A}{1+{{\cot }^{2}}A}=\dfrac{\dfrac{1}{{{\cos }^{2}}A}}{\dfrac{1}{{{\sin }^{2}}A}}$

$\Rightarrow \dfrac{1+{{\tan }^{2}}A}{1+{{\cot }^{2}}A}=\dfrac{{{\sin }^{2}}A}{{{\cos }^{2}}A}$

$\Rightarrow \dfrac{1+{{\tan }^{2}}A}{1+{{\cot }^{2}}A}={{\tan }^{2}}A$

Now, consider the RHS of the given expression, we get

$RHS={{\left( \dfrac{1-\tan A}{1-\cot A} \right)}^{2}}$

Now, we know that $\cot \theta =\dfrac{1}{\tan \theta }$, we get

$\Rightarrow {{\left( \dfrac{1-\tan A}{1-\cot A} \right)}^{2}}={{\left( \dfrac{1-\tan A}{1-\dfrac{1}{\tan A}} \right)}^{2}}$

$\Rightarrow {{\left( \dfrac{1-\tan A}{1-\cot A} \right)}^{2}}={{\left( \dfrac{1-\tan A}{\dfrac{\tan A-1}{\tan A}} \right)}^{2}}$

$\Rightarrow {{\left( \dfrac{1-\tan A}{1-\cot A} \right)}^{2}}={{\left( -\tan A \right)}^{2}}$

$\Rightarrow {{\left( \dfrac{1-\tan A}{1-\cot A} \right)}^{2}}={{\tan }^{2}}A$

Here, we get LHS=RHS

$\therefore \dfrac{1+{{\tan }^{2}}A}{1+{{\cot }^{2}}A}={{\left( \dfrac{1-\tan A}{1-\cot A} \right)}^{2}}$ 

Hence proved

NCERT Solutions for Class 10 Maths Chapter 8 - Summary

Introduction to Trigonometry

Trigonometry is all about triangles. It is all about right-angled triangles, triangles with one angle equal to 90 degrees, to be more precise. It's a method that helps us find a triangle's missing angles and missing sides. The ‘trigono’ word means triangle and the ‘metry’ word means to measure.

Trigonometric Ratios

In ΔABC, right-angled at ∠B, the trigonometric ratios of the ∠A are as follows:

• sin A=opposite side/hypotenuse=BC/AC

• cos A=adjacent side/hypotenuse=AB/AC

• tan A=opposite side/adjacent side=BC/AB

• cosec A=hypotenuse/opposite side=AC/BC

• sec A=hypotenuse/adjacent side=AC/AB

• cot A=adjacent side/opposite side=AB/BC

Standard Values of Trigonometric Ratios:

Trigonometric Identities: Trigonometric identities are essential tools in trigonometry for simplifying expressions, solving equations, and proving other mathematical statements.There are three Pythagorean trigonometric identities in trigonometry that are based on the right-triangle theorem or Pythagoras theorem.

• $\sin^2(x) + \cos^2(x) = 1$

• $1 + \tan^2(x) = \sec^2(x)$

• $\text{cosec}^2(x) = 1 + \cot^2(x)$

Overview of Deleted Syllabus for CBSE Class 10 Maths Chapter 8 Introduction to Trigonometry

Class 10 Maths Chapter 8: Exercise Breakdown

Conclusion

NCERT Solutions for Class 10 Maths Introduction to Trigonometry, provided by Vedantu, offer a comprehensive understanding of this foundational topic. By focusing on key concepts like trigonometric ratios, Pythagorean identities, and solving triangles, students can develop a strong foundation in trigonometry. Pay attention to the step-by-step solutions provided in the NCERT Solutions, as they help clarify concepts and reinforce problem-solving techniques. Understanding trigonometry is crucial as it forms the basis for more advanced topics in mathematics and has practical applications in fields like engineering, physics, and navigation. In previous years question papers, around  5-6 questions have been typically asked from this chapter.

Other Study Materials of CBSE Class 10 Maths Chapter 8

Chapter-Specific NCERT Solutions for Class 10 Maths

Given below are the chapter-wise NCERT Solutions for Class 10 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.

Study Resources for Class 10 Maths

For complete preparation of Maths for CBSE Class 10 board exams, check out the following links for different study materials available at Vedantu.