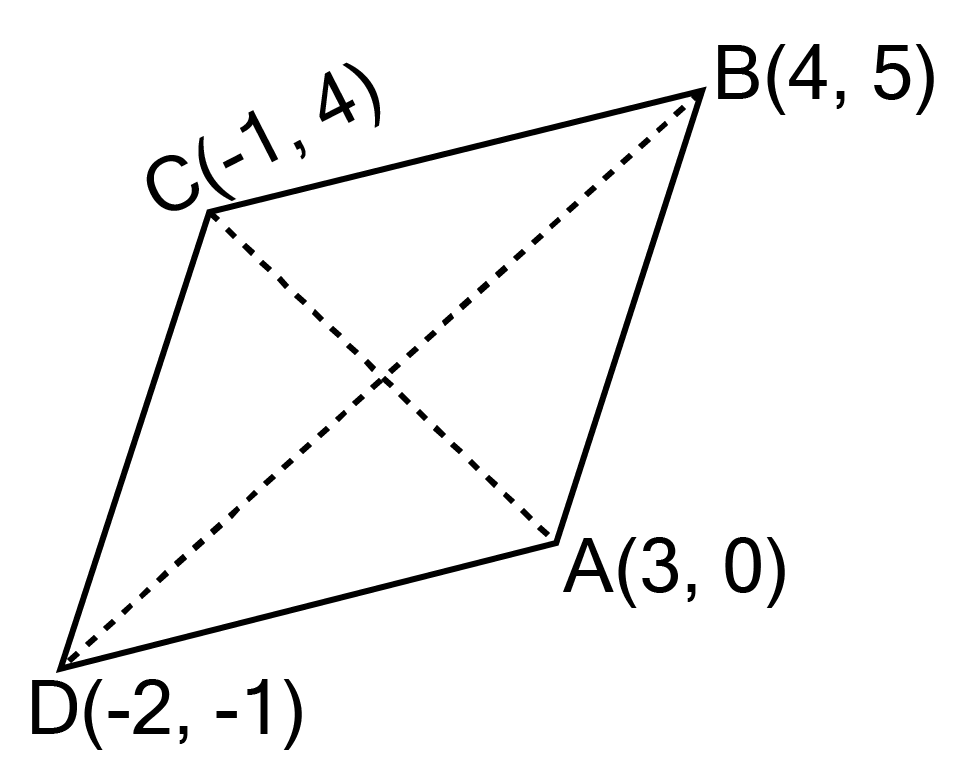
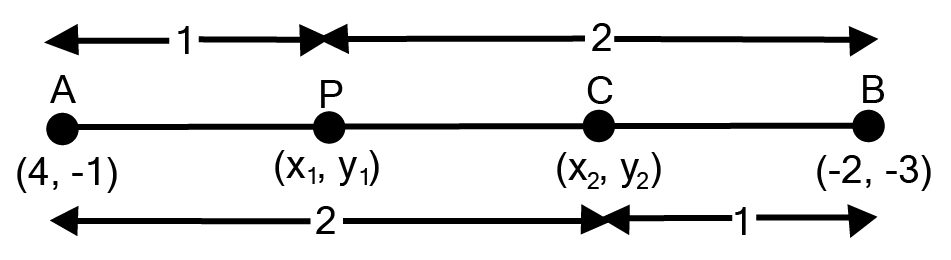
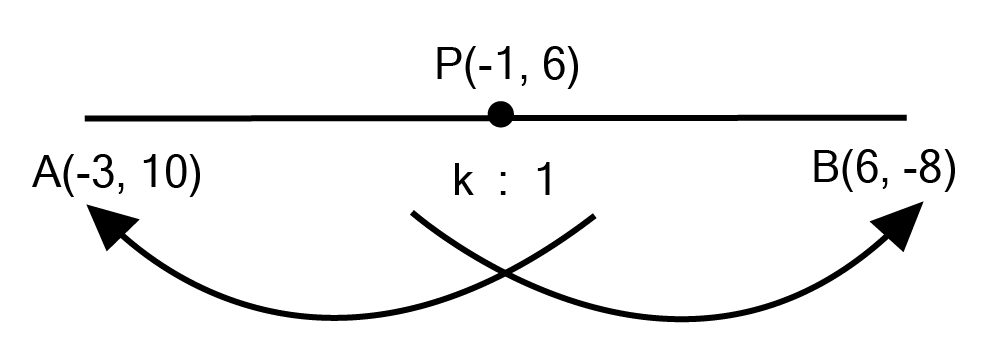
Find Class 10 Geometry Exercise 7.2 Solutions to Master Coordinate Geometry Problems
NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry
FAQs on NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry
1. What are the stepwise NCERT solutions for Class 10 Maths Chapter 7 Exercise 7.1?
The NCERT solutions for Class 10 Maths Chapter 7 Exercise 7.1 provide a stepwise explanation for each question, strictly following the CBSE 2025–26 format. Each answer uses the correct formulas such as the distance formula and midpoint formula, as per the official NCERT textbook, ensuring accurate and easy-to-understand solutions for all questions in Exercise 7.1.
2. How do I solve Exercise 7.2 of Class 10 Maths using the NCERT answer format?
To solve Exercise 7.2 of Class 10 Maths, use the coordinate geometry techniques provided in the NCERT textbook. Begin by reading each question carefully, apply the stepwise method involving section formula or area formula as required, and present all calculations clearly in CBSE-approved NCERT answer format for full marks according to the 2025–26 syllabus.
3. Does NCERT Solutions for Class 10 Maths Chapter 7 cover all intext and exercise questions?
Yes, NCERT Solutions for Class 10 Maths Chapter 7 comprehensively cover all intext and back exercise questions for coordinate geometry. These solutions are based on the latest NCERT pattern and include fully solved stepwise answers for exercises 7.1, 7.2, and 7.3 as per the CBSE guidelines.
4. Where can I find the official Class 10 Maths Chapter 7 Solution PDF as per NCERT?
The official Class 10 Maths Chapter 7 Solutions PDF, aligned with NCERT and CBSE 2025–26 standards, can be downloaded from trusted educational platforms like Vedantu. These PDFs include all stepwise solutions and match the NCERT textbook format for easy reference during exam preparation.
5. What method is used to solve Question 3 of Exercise 7.2 in NCERT Class 10 Maths?
Question 3 of Exercise 7.2 typically involves section formula or distance calculation. The NCERT answer format requires presenting every calculation step, starting from formula selection to the final answer, ensuring that logical reasoning and each mathematical step is clearly shown as per CBSE 2025–26 requirements.
6. Are the NCERT Solutions for Class 10 Maths Chapter 7 approved for CBSE board exams?
Yes, these NCERT Solutions are carefully prepared following the latest CBSE guidelines and are 100% suitable for board exams. Each solution is based on the NCERT textbook structure and ensures that students present their answers in CBSE-approved, stepwise format for full scoring.
7. Can I get Class 10 Maths Chapter 7 solutions in Hindi medium as per NCERT guidelines?
Yes, stepwise NCERT Solutions for Class 10 Maths Chapter 7 (Coordinate Geometry) are available in both English and Hindi mediums. The Hindi medium solutions are strictly aligned with the official NCERT structure and are updated for session 2025–26.
8. What are the benefits of using NCERT Solutions for coordinate geometry in Class 10?
Using NCERT Solutions for coordinate geometry helps students understand the concept through clear, stepwise methods, ensures they solve every question in the correct NCERT answer pattern, and builds confidence for CBSE board exams by practicing all types of questions found in textbook exercises.
9. How do NCERT Solutions for Chapter 7 help in solving application-based questions?
NCERT Solutions for Chapter 7 guide students through the application of formulas such as section formula, distance formula, and area of triangle in coordinate geometry, using a clear stepwise explanation. This helps in tackling both direct and application-based questions accurately as required in the CBSE exam pattern.
10. Are exercise solutions for 7.2 and 7.3 in Class 10 Maths based on the latest NCERT textbooks?
Yes, the solutions for exercises 7.2 and 7.3 in Class 10 Maths are thoroughly revised as per the latest NCERT textbooks and CBSE 2025–26 syllabus. Every answer is explained stepwise and includes all relevant calculation methods for coordinate geometry questions.
11. What is a common mistake students make while solving coordinate geometry problems in NCERT Class 10?
A frequent error is incorrect substitution of coordinates or steps skipped in calculation of distance, section, or area. Always follow the stepwise NCERT answer format and recheck each calculation to avoid marks deduction due to these mistakes as per CBSE standards.
12. How do stepwise NCERT Solutions improve accuracy in Class 10 Maths Chapter 7 answers?
Stepwise NCERT Solutions break down each problem in Class 10 Maths Chapter 7 into logical stages, helping students clearly see how the answer is constructed. This reduces confusion, ensures accuracy, and allows for proper CBSE marking as all method steps are shown, not just the final answer.




















 Watch Video
Watch Video



![the coordinates of the point which divides the join of \[{\text{( - 1,7)}}\] and \[{\text{(4, - 3)}}\]in the ratio \[{\text{2:3}}\]](https://www.vedantu.com/seo/content-images/1116dbaf-c72b-4a86-86f6-92ed1544e2a6.png)
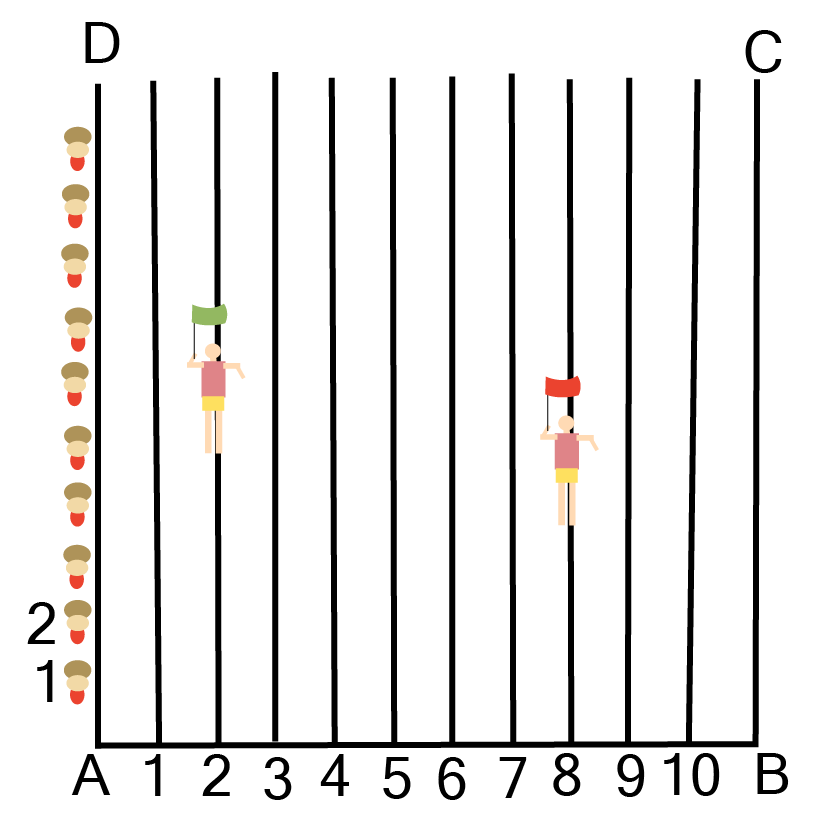


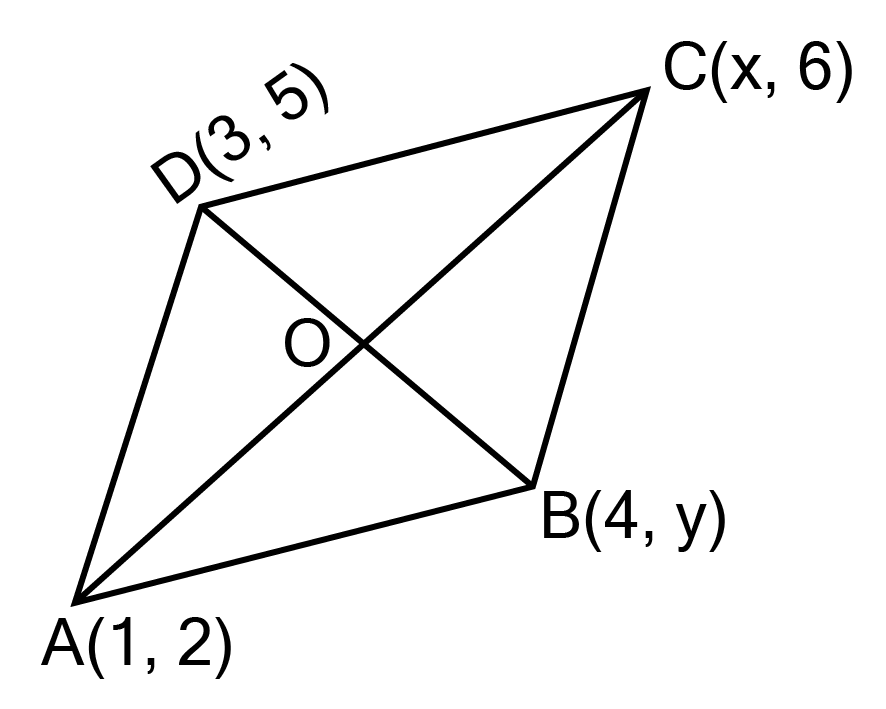
![The coordinates of a point A, where AB is the diameter of circle whose centre is\[{\text{(2, - 3)}}\] and B is\[{\text{(1,4)}}\]](https://www.vedantu.com/seo/content-images/67cf1131-f373-4a77-a2d9-27258c66dccd.png)
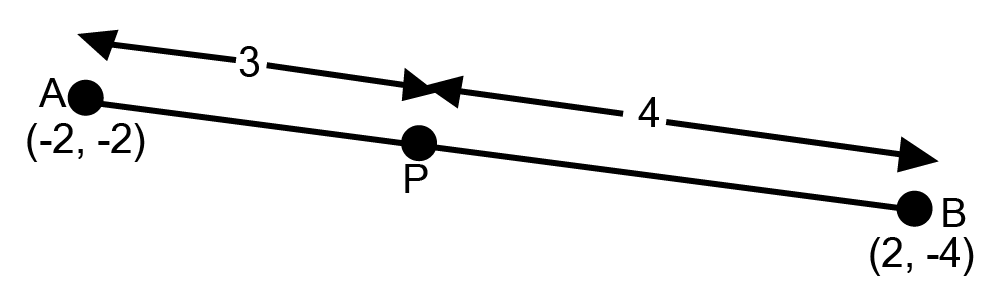
![The coordinates of the points which divide the line segment joining A\[{\text{( - 2,2)}}\] and B\[{\text{(2,8)}}\] into four equal parts](https://www.vedantu.com/seo/content-images/a0622883-3e03-4537-bef2-41f4f6643d98.png)