Watch Video
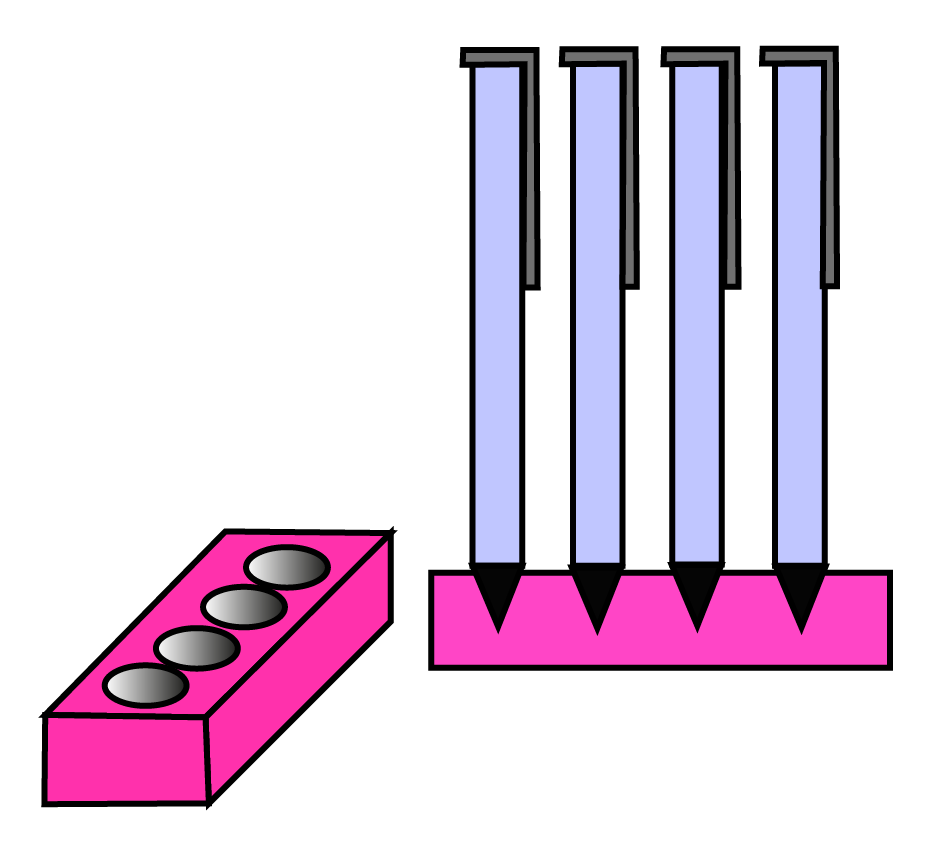
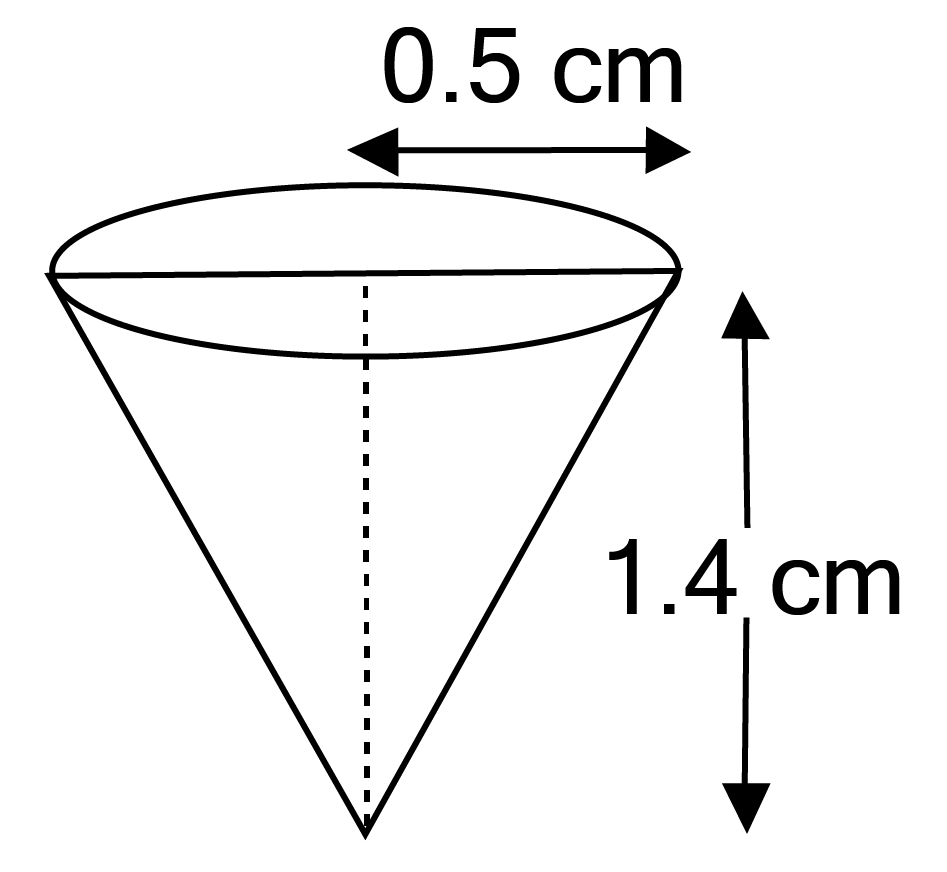
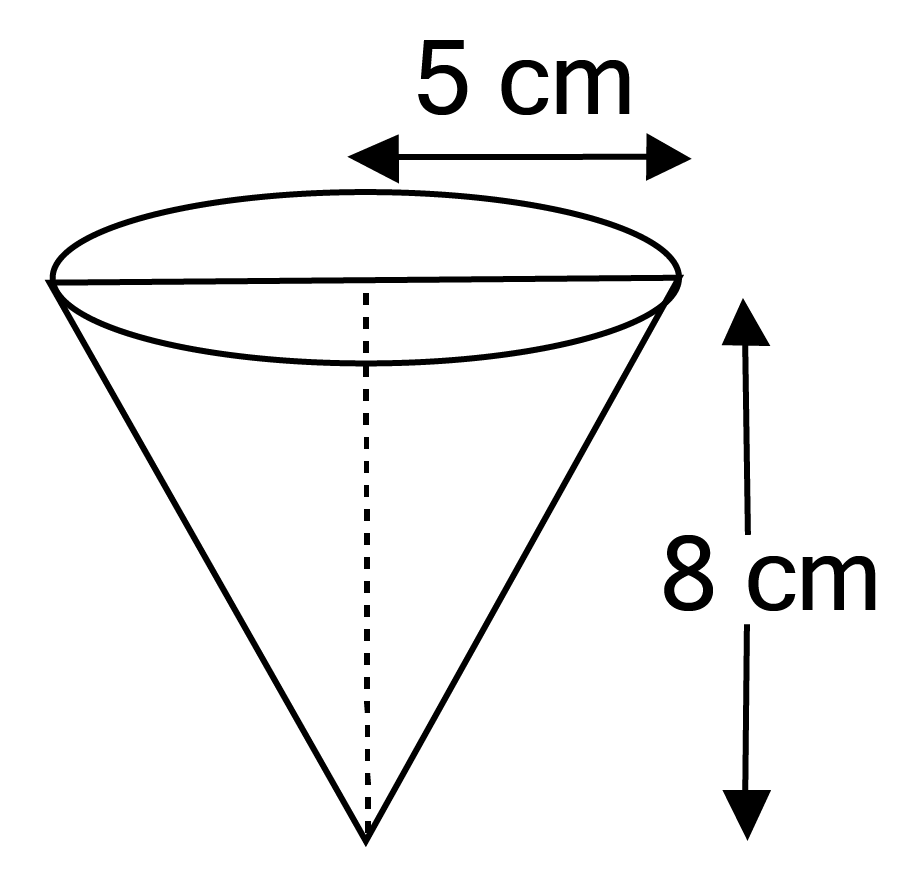
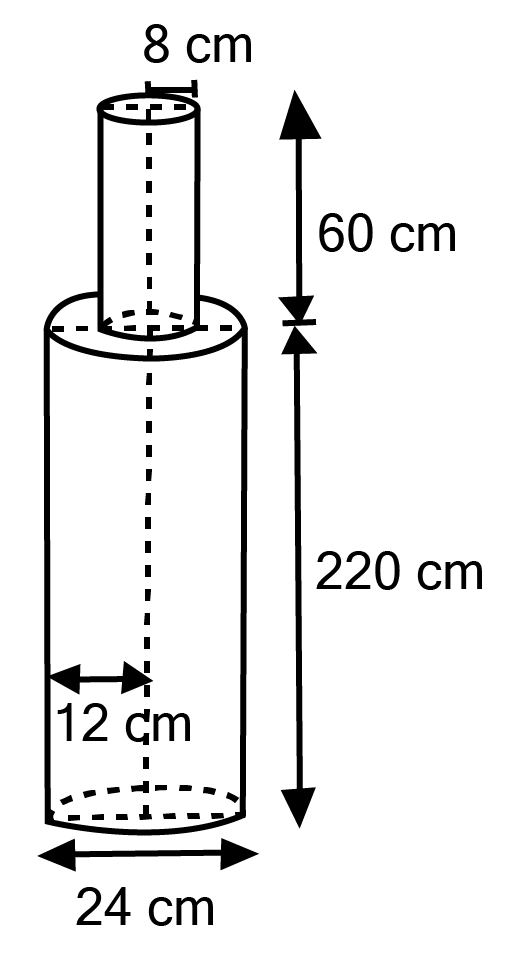
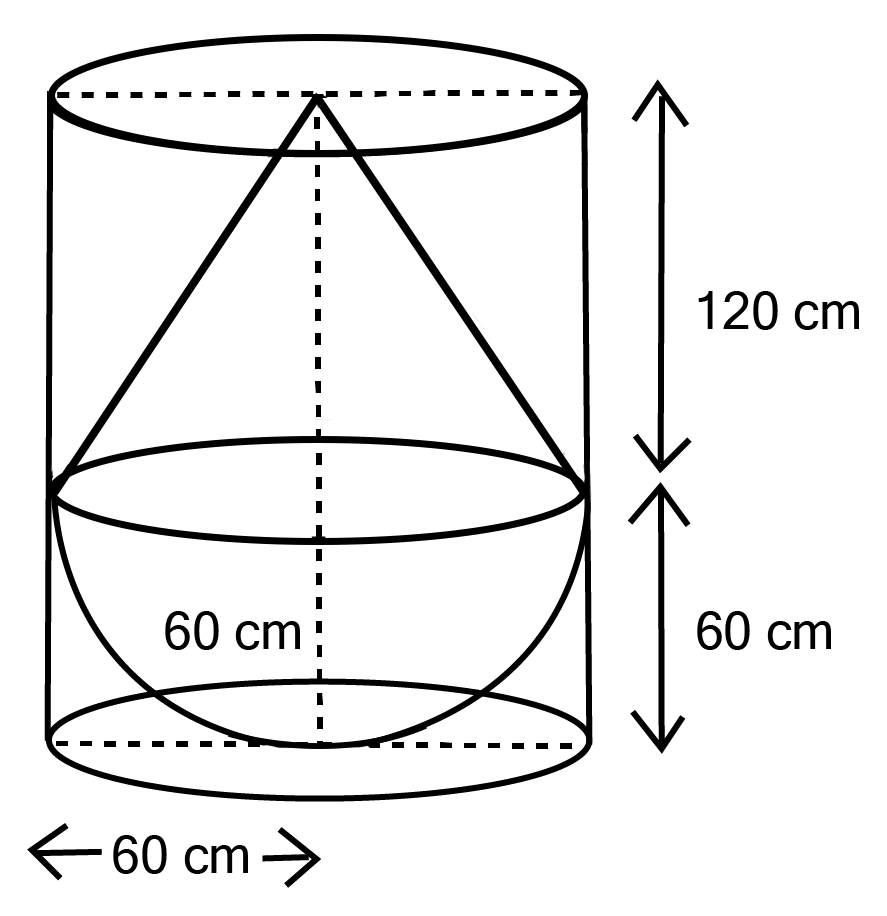
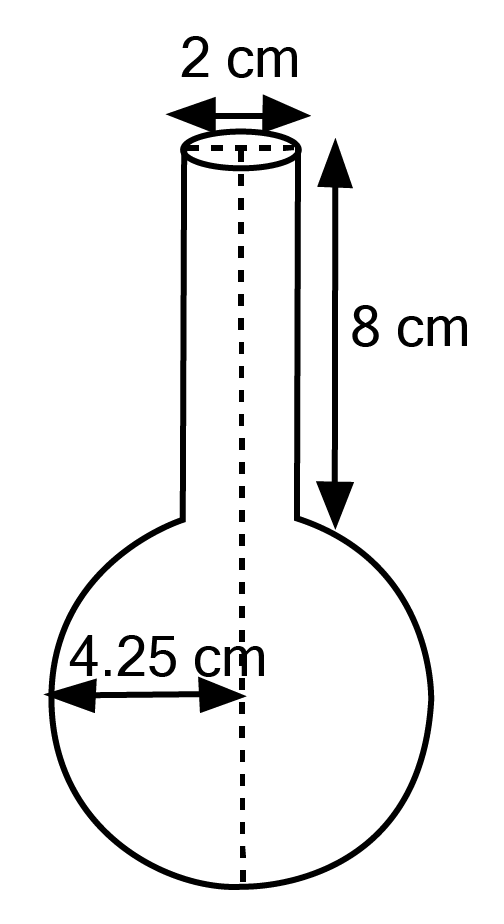
NCERT Solutions for Class 10 Maths Chapter 12 Exercise 12.2 - FREE PDF Download
You may download the PDF of Exercise 12.2 Class 10 Maths NCERT Solutions Chapter 12, Surface Areas and Volumes here. To help students better understand the topics, the knowledgeable maths professors at Vedantu have produced the class 10 Exercise 12.2 NCERT solutions PDF.
Table of Content
The subjects discussed in this page align with the most recent NCERT curriculum and recommendations. As a result, students feel that the NCERT Solutions for Maths Class 10 is a great resource for getting ready for and doing well on the CBSE Board exams.
Glance on NCERT Solutions Maths Chapter 12 Exercise 12.2 Class 10 | Vedantu
Solve problems where two or more basic 3D shapes (like cones, cylinders, spheres, cubes, etc.) are joined together.
Exercise 12.2 might include questions asking you to calculate the surface area and/or volume of various 3D shapes using the formulas it involves worded problems where you have to identify the 3D shape from the description and then apply the relevant formula.
Pay attention to the units (cm, m, etc.) while using the formulas.
Sketch a diagram of the 3D shape if it helps you visualize the problem.
Always pay attention to the specific instructions for each question. There are variations in the formulas depending on whether you need to calculate the total surface area (including the base) or the curved surface area only.
Formulas Used
Cube: Volume = a³, where a is the side length.
Cuboid: Volume = l × b × h, where l, b, and h are length, breadth, and height respectively.
Sphere: Volume = (4/3)πr³, where r is the sphere's radius.
Surface Area and Volume of Hemisphere
The volume of Hemisphere = (2πr^3)/3
Surface Area of Hemisphere = 3πr^2
Curved Surface Area of a Hemisphere = 2πr^2
The Formulas of Right Circular Cone are as follows:
Curved surface area of a cone = πr√(r^2 + h^2)
Volume of a Cone (V) = (1/3) × πr^2 × h
Total surface area of a cone = πr^2 + πr√(r^2 + h^2)
The Formulas for Cylinder are as Follows:
Curved surface area of cylinder = 2πrh
Total surface area of cylinder = 2πr(r+h)
The volume of a cylinder, V = πr^2h
NCERT Solutions for Class 10 Maths Chapter 12 Surface Areas And Volumes Ex 12.2
ShareShareClass 10 Ex 12.2
1. A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π.
Ans. From the given figure, we know that
Height (h) of conical part = Radius(r) of conical part \[{\text{ = 1cm}}\]
Radius(r) of hemispherical part = Radius of conical part (r) \[{\text{ = 1cm}}\]
Volume of solid = Volume of conical part + Volume of hemispherical part
\[{\text{ = }}\dfrac{1}{3}\pi {r^2}h + \dfrac{2}{3}\pi {r^3}\]
\[{\text{ = }}\dfrac{1}{3}\pi {\left( 1 \right)^2}\left( 1 \right) + \dfrac{2}{3}\pi {\left( 1 \right)^3} = \dfrac{{2\pi }}{3} + \dfrac{1}{3} = \pi {\text{c}}{{\text{m}}^3}\]
2. Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminum sheet. The diameter of the model is \[{\text{3cm}}\] and its length is\[{\text{12cm}}\]. If each cone has a height of \[{\text{2cm}}\], find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.)
Ans:
From the given figure, we know that
Height (h1) of each conical part \[{\text{ = 2cm}}\]
Height (h2) of cylindrical part \[{\text{ = 12 - 2}} \times {\text{ Height of conical part}}\]
\[{\text{ = 12 - 2}} \times {\text{2 = 8cm}}\]
Radius (r) of cylindrical part = Radius of conical part \[{\text{ = }}\dfrac{3}{2}{\text{cm}}\]
Volume of air present in the model = Volume of cylinder \[ + {\text{ }}2\, \times \]Volume of cones
\[ = \pi {r^2}{h_2} + 2 \times \dfrac{1}{3}\pi {r^2}{h_1}\]
\[ = \pi \times {\left( {\dfrac{3}{2}} \right)^2} \times 8 + 2 \times \dfrac{1}{3}\pi {\left( {\dfrac{3}{2}} \right)^2} \times 2\]
\[ = \pi \times \dfrac{9}{4} \times 8 + \dfrac{2}{3}\pi \times \dfrac{9}{4} \times 2\]
\[ = 18\pi + 3\pi = 21\pi = 66{\text{c}}{{\text{m}}^3}\]
3. A gulab jamun, contains sugar syrup up to about 30% of its volume. Find approximately how much syrup would be found in 45 gulab jamuns, each shaped like a cylinder with two hemispherical ends with length 5 cm and diameter 2.8 cm (see the given figure).
Ans:
We can observe that,
Radius (r) of cylindrical part = Radius (r) of hemispherical part
\[{\text{ = }}\dfrac{{{\text{2}}{\text{.8}}}}{{\text{2}}}{\text{ = 1}}{\text{.4cm}}\]
Length of each hemispherical part = Radius of hemispherical part \[{\text{ = 1}}{\text{.4cm}}\]
Length (h) of cylindrical part \[{\text{ = 5 - }}\,{\text{2}} \times {\text{Length of hemispherical part }}\]
\[{\text{ = 5 - }}\,{\text{2}} \times {\text{1.4 = 2}}{\text{.2cm}}\]
Volume of one gulab jamun = Vol. of cylindrical part + 2 × Vol. of hemispherical part
\[ = \pi {r^2}h + 2 \times \dfrac{2}{3}\pi {r^3} = \pi {r^2}h + \dfrac{4}{3}\pi {r^3}\]
\[ = \pi {\left( {1.4} \right)^2}\left( {2.2} \right) + \dfrac{4}{3}\pi {\left( {1.4} \right)^3}\]
\[ = \dfrac{{22}}{7} \times 1.4 \times 1.4 \times 2.2 + \dfrac{4}{3} \times \dfrac{{22}}{7} \times 1.4 \times 1.4 \times 1.4\]
\[{\text{ = 13}}{\text{.552 + 11}}{\text{.498 = 25}}{\text{.05c}}{{\text{m}}^{\text{3}}}\]
Volume of \[{\text{45}}\] gulab jamuns \[{\text{ = 45}} \times {\text{25}}{\text{.05 = 1127}}{\text{.25c}}{{\text{m}}^{\text{3}}}\]
Volume of sugar syrup \[ = 30\% \] of volume
\[ = \dfrac{{30}}{{100}} \times 1127.25\]
\[{\text{ = 338}}{\text{.17c}}{{\text{m}}^{\text{3}}}\]
\[ \cong {\text{338c}}{{\text{m}}^{\text{3}}}\]
4. A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboids are \[{\text{15cm}}\] by \[{\text{10cm}}\] by \[{\text{3}}{\text{.5cm}}\]. The radius of each of the depressions is \[{\text{0}}{\text{.5cm}}\] and the depth is \[{\text{1}}{\text{.4cm}}\]. Find the volume of wood in the entire stand (see the following figure).
Ans:
Depth (h) of each conical depression\[{\text{ = 1}}{\text{.4cm}}\]
Radius (r) of each conical depression\[{\text{ = 0}}{\text{.5cm}}\]
Volume of wood = Volume of cuboid \[ - {\text{ }}4 \times \] Volume of cones
\[{\text{ = l * b * h}}\]\[ - 4 \times \dfrac{1}{3}\pi {r^2}h\]
\[ = 15 \times 10 \times 3.5 - 4 \times \dfrac{1}{3} \times \dfrac{{22}}{7} \times {\left( {\dfrac{1}{2}} \right)^2} \times 1.4\]
\[ = 525 - 1.47\]
\[{\text{ = 523}}{\text{.53c}}{{\text{m}}^{\text{3}}}\]
5. A vessel is in the form of an inverted cone. Its height is \[{\text{8cm}}\] and the radius of its top, which is open, is \[{\text{5cm}}\]. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius \[{\text{0}}{\text{.5cm}}\]are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.
Ans:
Height (h) of conical vessel\[{\text{ = 8cm}}\]
Radius (r1) of conical vessel\[{\text{ = 5cm}}\]
Radius (r2) of lead shots\[{\text{ = 0}}{\text{.5cm}}\]
Let the number of lead shots dropped in the vessels be n.
Volume of water spilled = Volume of dropped lead shots
\[\dfrac{1}{4} \times \]Volume of cone \[{\text{ = n *}}\dfrac{{\text{4}}}{{\text{3}}}{{\text{r}}_{\text{2}}}^{\text{3}}\]
\[\dfrac{1}{4} \times \dfrac{1}{3}\pi {{\text{r}}_1}^2{\text{h = n * }}\dfrac{{\text{4}}}{{\text{3}}}{{\text{r}}_{\text{2}}}^{\text{3}}\]
\[{{\text{r}}_1}^2{\text{h = n *16}}{{\text{r}}_{\text{2}}}^{\text{3}}\]
\[{5^2} \times {\text{8 = n *16}} \times {\left( {0.5} \right)^{\text{3}}}\]
\[n = \dfrac{{25 \times 8}}{{16 \times {{\left( {\dfrac{1}{2}} \right)}^3}}} = 100\]
Therefore, the number of lead shots dropped in the vessel is \[100\]
6. A solid iron pole consists of a cylinder of height \[{\text{220cm}}\] and base diameter \[{\text{24cm}}\], which is surmounted by another cylinder of height \[{\text{60cm}}\] and radius \[{\text{8cm}}\]. Find the mass of the pole, given that \[{\text{1c}}{{\text{m}}^3}\]of iron has approximately \[{\text{8g}}\] mass.
Ans:
From the above figure, we observe that
Height (h1) of larger cylinder \[{\text{ = 220cm}}\]
Radius (r1) of larger cylinder \[{\text{ = }}\dfrac{{24}}{2}{\text{ = 12cm}}\]
Height (h2) of smaller cylinder \[{\text{ = 60cm}}\]
Radius (r2) of smaller cylinder \[{\text{ = 8cm}}\]
Total volume of pole = Volume of larger cylinder + volume of smaller cylinder
\[{\text{ =}}\pi{{\text{r}}_{\text{1}}}^{\text{2}}{{\text{h}}_{\text{1}}}{\text{ +}} \pi {{\text{r}}_{\text{2}}}^{\text{2}}{{\text{h}}_{\text{2}}}\]
\[{\text{ = }} \pi {\left( {12} \right)^{\text{2}}}* {\text{220 + }} \pi {\left( 8 \right)^{\text{2}}} * 60\]
${\text{ = }}\pi\left[ {{\text{(144 * 220) + (64 * 60)}}} \right] $
${\text{ = 35520 * 3}}{\text{.14 = 111532}}{\text{.8c}}{{\text{m}}^{\text{3}}} $
Mass of \[{\text{1c}}{{\text{m}}^3}\]iron = \[{\text{8g}}\]
Mass of \[{\text{111532}}{\text{.8c}}{{\text{m}}^{\text{3}}}\]iron \[{\text{ = 111532}}{\text{.8 * 8 = 892262}}{\text{.4g = 892}}{\text{.262kg}}\]
7. A solid consisting of a right circular cone of height \[{\text{120cm}}\] and radius \[{\text{60cm}}\] standing on a hemisphere of radius \[{\text{60cm}}\] is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is \[{\text{60cm}}\] and its height is \[{\text{180cm}}\].
Ans:
Radius (r) of hemispherical part = Radius (r) of conical part\[{\text{ = 60cm}}\]
Height (h2) of conical part of solid\[{\text{ = 120cm}}\]
Height (h1) of cylinder\[{\text{ = 180cm}}\]
Radius (r) of cylinder\[{\text{ = 60cm}}\]
Volume of water left = Volume of cylinder − Volume of solid
= Volume of cylinder – (Volume of cone + Volume of hemisphere)
\[{\text{ = }}\pi{{\text{r}}^{\text{2}}}{{\text{h}}_{\text{1}}}{\text{ - }}\left( {\dfrac{{\text{1}}}{{\text{3}}}{\pi}{{\text{r}}^{\text{2}}}{{\text{h}}_{\text{2}}}{\text{ + }}\dfrac{{\text{2}}}{{\text{3}}} \pi {{\text{r}}^{\text{3}}}} \right)\]
\[{\text{ = }}\pi {\left( {60} \right)^{\text{2}}} \times 180{\text{ - }}\left( {\dfrac{{\text{1}}}{{\text{3}}}{\pi }{{\left( {60} \right)}^{\text{2}}} \times {\text{120 + }}\dfrac{{\text{2}}}{{\text{3}}}{\pi }{{\left( {60} \right)}^{\text{3}}}} \right)\]
\[{\text{ = }}\pi{\left( {60} \right)^{\text{2}}}\left[ {\left( {180} \right) - \left( {40 + 40} \right)} \right]\]
\[{\text{ = }}\pi\left( {{\text{3600}}} \right)\left( {{\text{100}}} \right){\text{ = 3,60,000 }}\pi{\text{c}}{{\text{m}}^{\text{3}}}{\text{ = 11311428}}{\text{.57c}}{{\text{m}}^{\text{3}}}{\text{ = 1}}{\text{.131}}{{\text{m}}^{\text{3}}}\]
8. A spherical glass vessel has a cylindrical neck \[{\text{8cm}}\] long, \[{\text{2cm}}\] in diameter; the diameter of the spherical part is \[{\text{8}}{\text{.5cm}}\]. By measuring the amount of water it holds, a child finds its volume to be \[{\text{345c}}{{\text{m}}^3}\]. Check whether she is correct, taking the above as the inside measurements, and \[\pi = 3.14\].
Ans:
Height (h) of cylindrical part \[{\text{ = 8cm}}\]
Radius (r2) of cylindrical part \[{\text{ = }}\dfrac{2}{2}{\text{ = 1cm}}\]
Radius (r1) spherical part \[{\text{ = }}\dfrac{{8.5}}{2}{\text{ = 4}}{\text{.25cm}}\]
Volume of vessel = Volume of sphere + Volume of cylinder \[{\text{ = }}\dfrac{4}{3}\pi {\left( {\dfrac{{8.5}}{2}} \right)^3}{\text{ + }}\pi {\left( 1 \right)^2}\left( 8 \right)\]
\[{\text{ = }}\dfrac{4}{3} \times 3.14 \times 76.765625{\text{ + 8}} \times {\text{3}}{\text{.14}}\]
\[ = 321.392 + 25.12\]
\[ = 346.512\]
\[{\text{ = 346}}{\text{.51c}}{{\text{m}}^{\text{3}}}\]
Therefore, she is wrong.
Conclusion
Ex 12.2 Class 10 Maths Chapter 12, Surface Areas and Volumes, is all about the volumes of different solid shapes and how they can be combined. Understanding how to compute the volumes of various geometric solids, such as cubes, cuboids, cylinders, cones, and spheres, as well as their combinations, requires completion of this task. For detailed solutions and step-by-step explanations, refer to the NCERT Solutions provided by Vedantu.
Class 10 Maths Chapter 12: Exercises Breakdown
CBSE Class 10 Maths Chapter 12 Other Study Materials
Chapter-Specific NCERT Solutions for Class 10 Maths
Given below are the chapter-wise NCERT Solutions for Class 10 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.
Study Resources for Class 10 Maths
For complete preparation of Maths for CBSE Class 10 board exams, check out the following links for different study materials available at Vedantu.
FAQs on NCERT Solutions for Class 10 Maths Chapter 12 Surface Areas And Volumes Ex 12.2
1. What are the key topics covered in the NCERT Solutions for Class 10 Maths Chapter 12 Surface Areas and Volumes?
The NCERT Solutions for Class 10 Maths Chapter 12 focus on:
- Surface areas and volumes of basic 3D shapes (cube, cuboid, cylinder, cone, sphere, hemisphere)
- Calculating combined surface area and volume for composite solids
- Conversion of one solid shape into another
- Problems on frustum of a cone
2. How do the NCERT Solutions for Class 10 Maths Chapter 12 ensure accuracy in solving surface area and volume questions?
NCERT Solutions apply formulas systematically, provide stepwise calculations, and clarify unit conversions. Diagrams are often used to help visualize 3D shapes, and all answers adhere strictly to the latest CBSE exam pattern for Class 10 Maths.
3. What common mistakes should students avoid when solving problems from Chapter 12 Surface Areas and Volumes?
Students should avoid:
- Mixing up formulas for similar shapes (e.g., using volume formula for surface area)
- Forgetting to convert all measurements to the same units before calculation
- Ignoring whether the question asks for total or curved surface area
- Not reading scenario-based questions carefully about composite solids
4. How is the combination of solids concept applied in Class 10 Maths Chapter 12 NCERT Solutions?
In combination of solids problems, students calculate the required measure (volume or surface area) for each basic shape and then add or subtract as per the specific question's composite figure. The solutions clarify which parts to include or remove, aiding clarity in approach.
5. What are the important formulas for Surface Areas and Volumes Class 10 Chapter 12 that appear in NCERT Solutions?
Key formulas include:
- Cube volume: a³
- Cuboid volume: l × b × h
- Sphere volume: (4/3)πr³
- Cylinder volume: πr²h
- Cone volume: (1/3)πr²h
- Surface Area (various shapes) and formulas for combination and frustum as per CBSE Class 10 Maths syllabus
6. Why is unit consistency crucial in NCERT Solutions for Class 10 Maths Chapter 12 questions?
Unit consistency is essential to avoid calculation errors. All measurements (length, area, volume) must use the same units before applying formulas. The solutions always highlight this check, ensuring full marks during CBSE evaluation.
7. What strategies help visualize and solve complex 3D problems in Class 10 Surface Areas and Volumes?
Drawing labelled diagrams for each question, clearly marking dimensions, and identifying the shapes involved, helps break down the problem. The solutions guide students in mapping textual data to real figures for better comprehension.
8. How can students distinguish between surface area and volume in NCERT Class 10 Maths Chapter 12?
Surface area measures the external covering of a solid, calculated in square units (cm², m²), while volume is the space a solid occupies, measured in cubic units (cm³, m³). NCERT Solutions include explicit examples to help reinforce this distinction with various 3D shapes.
9. In what ways are composite shapes handled in NCERT Solutions for Class 10 Maths Chapter 12?
The solutions first separate each basic shape (cylinder, cone, hemisphere, etc.) forming the composite, calculate their respective volumes or surface areas, then use addition or subtraction as the scenario instructs, matching the latest CBSE problem-solving approach.
10. Are the NCERT Solutions for Chapter 12 Surface Areas and Volumes sufficient for CBSE Board preparation?
Yes, the NCERT Solutions address every exercise problem as per CBSE 2025–26 syllabus, reinforce conceptual clarity, and are recommended by teachers and top scorers for complete board exam preparation.
11. What is the process to solve frustum-related questions in NCERT Solutions for Class 10 Maths Chapter 12?
For frustums, the solutions use specific formulas for volume and surface area of a frustum of a cone and substitute given values from the question stepwise. Formula memorization and understanding shape structure are both emphasized in the explanations.
12. How does Chapter 12 link to real-world applications as per NCERT Solutions?
Chapter 12 connects 3D geometry to daily life, such as calculating paint needed for a tank, volume of containers, or surface area for wrapping. The solutions often relate questions to practical examples, enhancing understanding and applicability.
13. How should students approach word problems in NCERT Solutions for Class 10 Maths Chapter 12?
Students should:
- Identify all shapes and measurements from the problem statement
- Sketch diagrams if possible
- Select and apply correct formulas
- Check for required final units before stating the answer
14. What conceptual understanding is tested by HOTS questions in Surface Areas and Volumes?
Higher Order Thinking Skills (HOTS) questions test ability to:
- Analyze and decompose complex composite solids
- Apply formulas in unconventional ways
- Reason out conversions (e.g., melting and recasting solids)
- Justify or verify correctness of real-world numerical data involving surface area and volume
15. Why is it important to study every exercise, not just selective questions, in NCERT Solutions for Class 10 Maths Chapter 12?
Every exercise targets a different aspect of surface area and volume—from simple computation to word problems, HOTS, and real-life context. Studying all exercises ensures comprehensive understanding, which is essential for excelling in CBSE Class 10 board exams.
