




Introduction to Round Off
Rounding is the process of replacing a number with an approximation that has a shorter, simpler, or more accurate description. For instance, changing 23.4476 to 23.45, 312/937 to 1/3, or 2 to 1.414. Rounding is frequently done to get a value that is simpler to report and explain than the original. For example, a quantity that was computed as 123,456 but is known to be accurate to within a few hundred units is usually better stated as "about 123,500." On the other hand, rounding exact numbers will result in a small amount of round-off error being reported. When reporting many computations, rounding is essentially unavoidable, especially when dividing two numbers in integer or fixed-point arithmetic, computing mathematical functions like sines, square roots, and logarithms, or using a floating-point representation with a fixed number of significant digits. In a series of calculations, these rounding errors typically add up and, in some unfortunate circumstances, they might represent the outcome meaninglessly.

Rules of Rounding Numbers
Round Off
When a number is rounded off, its value is maintained but is moved closer to the following number, simplifying the number. It is done for whole numbers as well as decimals at different places such as hundreds, tens, tenths, etc. To maintain the significant figures, numbers are rounded off. Simply put, the number of figures that are known with some degree of reliability is the number of significant figures in a result.
According to legend, the number 13.2 contains three significant figures. Digits greater than zero are always important. There are six significant digits in the number 3.14159. (all the numbers give you useful information). As a result, 67 has two significant digits, while 67.3 has three.
How to Round off Decimal Numbers?
Rounding rules for decimal numbers are as follows:
Determine the rounding digit and look at its right-hand side.
If the digits on the right-hand side are less than 5, consider them equal to zero.
If the digits on the right-hand side are greater than or equal to 5, then add +1 to that digit and consider all other digits as zero.

Decimal Round off
How to Round off Whole Numbers?
Rounding rules for whole numbers are as follows:
To get an accurate final result, always choose the smaller place value.
Look for the next smaller place which is towards the right of the number that is being rounded off. For example, if you are rounding off a digit from a tens place, look for a digit in one place.
If the digit in the smallest place is less than 5, then the digit is left untouched. Any number of digits after that number becomes zero and this is known as rounding down.
If the digit in the smallest place is greater than or equal to 5, then the digit is added with +1. Any digits after that number become zero and this is known as rounding up.

Whole Number Round Off
Rounding off to the Nearest Ten
A good way of explaining this is to use a number line.
If the unit of the number is less than five, the number needs to be rounded down.
If the unit of the number is 5 or above, the number needs to be rounded up.
So 32 would be rounded down to 30, 35 would be rounded up to 40 and 38 would also be rounded up to 40:
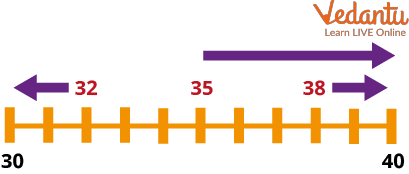
Number Line
Rounding off to the Nearest Hundred
If the tens digit is less than 50 the number is rounded down.
If the tens digit is 50 or more, the number is rounded up. (The unit digit can be ignored when rounding a three-digit number to the nearest 100.)
So 834 would be rounded down to 800, 851 would be rounded up to 900 and 876 would be rounded up to 900:
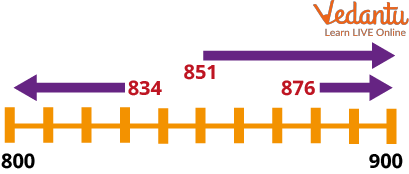
Number Line From 800 to 900
Summary
Round-off errors of a tiny amount will be reported when accurate figures are rounded. Rounding is essentially inevitable when summarising a large number of calculations, particularly when dividing two numbers in fixed-point or integer arithmetic, computing mathematical functions like sines, square roots, and logarithms, or using a floating-point representation with a fixed number of significant digits. These rounding errors usually mount up in a succession of calculations and, in some terrible cases, they could render the result meaningless.
FAQs on Round Off - A Fun Learning
1. What does it mean to “round off” a number?
Rounding off means replacing a number with a simpler, approximate value that is close to the original. It makes numbers easier to work with, report, and understand. For example, instead of using 298, you might round it off to 300 to quickly estimate a total.
2. What are the general rules for rounding whole numbers?
To round off whole numbers, you first identify the place value you are rounding to (like tens or hundreds). Then, you look at the digit to its immediate right. The rules are:
- If the digit to the right is less than 5 (0, 1, 2, 3, or 4), you round down. The digit in the rounding place stays the same, and all digits to its right become zero.
- If the digit to the right is 5 or greater (5, 6, 7, 8, or 9), you round up. You add one to the digit in the rounding place, and all digits to its right become zero.
3. How do you round a number to the nearest ten, with an example?
When rounding to the nearest ten, you look at the digit in the ones place. For example, to round the number 67:
- The digit in the ones place is 7.
- Since 7 is greater than 5, we round up.
- We add 1 to the tens digit (6+1=7) and the ones digit becomes 0.
- So, 67 rounded to the nearest ten is 70.
4. How do you round a number to the nearest hundred?
To round to the nearest hundred, you focus on the digit in the tens place. For example, with the number 834:
- The digit in the tens place is 3.
- Since 3 is less than 5, we round down.
- The hundreds digit (8) stays the same, and the tens and ones digits become zero.
- So, 834 rounded to the nearest hundred is 800.
5. What is the special rule for rounding off when a digit is exactly 5? For instance, is 45 rounded to 40 or 50?
The special rule for a digit that is exactly 5 is to always round up. This is a key principle in rounding. So, when rounding the number 45 to the nearest ten, you look at the 5 in the ones place. Because the rule is to round up for 5 or greater, 45 is rounded up to 50.
6. Why is rounding off numbers a useful skill in everyday life?
Rounding is very useful in real life because it helps us make quick calculations and estimations. For example, when you are shopping, you can round the prices of items to the nearest ten or hundred to quickly estimate the total bill. It is also used for estimating time, distance, or quantities when an exact number isn't necessary.
7. How is rounding to the nearest hundred different from rounding to the nearest ten?
The main difference is the digit you look at to make your decision. When rounding to the nearest ten, you examine the ones digit. However, when rounding to the nearest hundred, you ignore the ones digit and examine the tens digit to decide whether to round up or down. The target place value determines which digit guides the rounding process.
8. What are some fun ways to practice rounding numbers?
You can make rounding practice fun by using real-world items. For example:
- Shopping Game: Use a grocery flyer, round the price of each item to the nearest ten, and estimate the total cost.
- Number Line Hop: Draw a number line on the floor with chalk. Call out a number and hop to the nearest ten or hundred.
- Card Game: Draw two or three number cards to create a number, then flip another card to decide whether to round up (if it's 5-9) or down (if it's 0-4).









