




How to Find LCM of 3 Numbers Easily with Step-by-Step Solutions
The least common multiple (LCM) is the smallest positive integer that is divided by both a and b. Its official name is Least Common Multiple.
The LCM method is used to determine the least multiple of two or more numbers. Both of the numbers will divide the LCM. When performing any arithmetic operations involving fractions, such as addition and subtraction, LCM is utilized to make the denominators common. This method facilitates the simplification process.
What is LCM?
When the denominators of two fractions are different, LCM can also be used to add or subtract the fractions. The smallest positive integer that is divided by both a and b is known as the least common multiple (LCM) .A number that is a multiple of two or more other numbers is said to be a common multiple.
LCM with 3 Numbers:
LCM is represented as LCM for three integers a, b, and c. For instance, the smallest number that can be divided by all three integers is 60, which is the LCM of 12, 15, and 10. \[{\rm{LCM}}\left[ {12,15,10} \right]\] thus equals 60.
How to Calculate LCM of Three Numbers:
To find 3 Numbers LCM with Listing Multiples:
This is a very interesting process to How to Take the LCM of 3 Numbers:
List every multiple of three numbers until at least one of them appears on every list.
Find the number that appears on all of the lists and is the least.

LCM of 3 Numbers Formula(for 8, 4, 6)
Utilizing Prime Factorization, get the LCM of Three Numbers:
Make a list of each of the provided numbers' prime factors.
List all the prime numbers you've discovered, in order of how frequently they appear in the given numbers.
To find the Least Common Multiple, multiply the list of prime numbers.
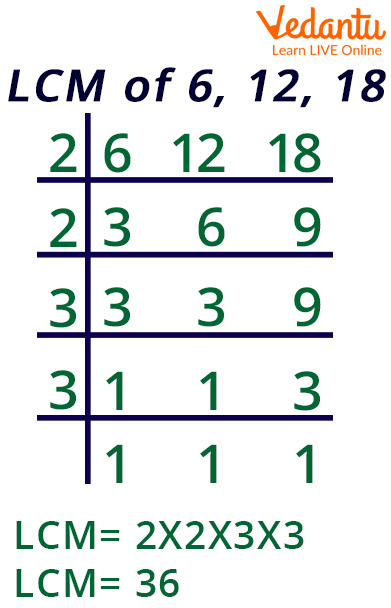
LCM of 6,12,18
Find LCM of Numbers Using Cake/ Ladder Method:
Put the three numbers in a row or cake pattern.
Bring the result into the following layer after dividing the integers in the layer by the given number that is equally divisible by all those numbers present.
Simply bring any non-divisible number down if it is present in the layer or row.
Divide the rows by prime numbers once more.
You are finished when there are no more numbers.
Then, multiply all the numbers together and you will get the LCM of required numbers.
Properties of LCM:
PROPERTY 1 : LCM obeys Associative Property
\[{\rm{LCM}}\left[ {c,d} \right] = {\rm{LCM}}\left[ {d,c} \right]\]
PROPERTY 2 : LCM obeys Commutative Property
\[{\rm{LCM}}\left[ {a,b,c} \right] = {\rm{LCM}}\left[ {{\rm{LCM}}\left[ {a,b} \right],c} \right] = {\rm{LCM}}\left[ {a,{\rm{LCM}}\left[ {b,c} \right]} \right]\]
PROPERTY 3 : LCM obeys Distributive Property
\[{\rm{LCM}}\left[ {da,db,dc} \right] = d \times {\rm{LCM}}\left[ {a,b,c} \right]\]
Conclusion
LCM can be used to add or subtract two fractions when their respective denominators are different. The least common multiple (LCM) is the smallest positive integer that is divided by both a and b. (LCM).
Solved Example :
Example 1 : Find \[{\rm{LCM}}\left[ {6,7,21} \right]\] by listing Multiples.
Solution : Given digits 6, 7, and 21
There are six multiples: 6, 12, 18, 24, 30, 36, 42, 48, 54, and 60
7 is a multiple of 14, 21, 28, 35, 42, 49, and 56.
21 is a multiple of 21, 42, and 63.
According to the definition, the least common multiple [LCM] of all three integers is the smallest number.
Thus, the LCM of 6, 7, and 21 is 42.
Example 2 : Find LCM of 12, 24, 30 using Prime Factorization Method?
Solution : 12's prime factorization is \[2 \times 2 \times 3\]
24's prime factorization is \[2 \times 2 \times 2 \times 2 \times 3\]
prime factorization of 30 will be \[2 \times 3 \times 5\]
Make a note of the often occurring prime numbers for the provided numbers, then multiply them.
\[ = 2 \times 2 \times 2 \times 3 \times 5\]
\[ = 120\]
Thus, its LCM of given numbers is 120.
Example 3 : Find the LCM(10, 12, 15) using the Cake/ Ladder Method.
Solution : Numbers given are 10, 12, and 15.

LCM of 10,12,15 by Cake/Ladder Method
Using a Cake and Ladder
To locate LCM From top to bottom, multiply all the prime integers, i.e.
\[2 \times 3 \times 5 \times 1 \times 2 \times 1 = 60\]
LCM(10, 12, 15) is therefore 60.
FAQs on LCM with 3 Numbers: Guide, Methods & Practice
1. What is the definition of the Least Common Multiple (LCM) in mathematics?
The Least Common Multiple (LCM) of three or more numbers is the smallest positive integer that is a multiple of all the given numbers. In other words, it is the smallest number that can be divided by all three numbers without leaving a remainder.
2. How do you find the LCM of three numbers using the prime factorization method?
To find the LCM of three numbers using the prime factorization method, you follow these steps:
- Step 1: Find the prime factors of each of the three numbers.
- Step 2: List all the unique prime factors that appear in any of the factorizations.
- Step 3: For each unique prime factor, identify the highest power it is raised to in any of the three factorizations.
- Step 4: Multiply these highest powers together to get the LCM.
3. Can you explain the division method for finding the LCM of three numbers?
The division method, also known as the ladder or tabular method, is a systematic way to find the LCM of three numbers:
- Step 1: Arrange the three numbers in a row.
- Step 2: Divide them by the smallest prime number that divides at least one of the numbers.
- Step 3: Write the quotients and any undivided numbers in the next row.
- Step 4: Continue this process until the quotients in the last row are all 1.
- Step 5: The LCM is the product of all the prime divisors used in the process.
4. What is a real-world example of using the LCM of three numbers?
A common real-world application of LCM is in scheduling events that repeat at different intervals. For example, if three different lighthouses flash their lights every 3 seconds, 4 seconds, and 5 seconds, respectively, the LCM of 3, 4, and 5 will determine when they will all flash at the same time. The LCM(3, 4, 5) is 60. This means all three lighthouses will flash together every 60 seconds.
5. How is finding the LCM for three numbers different from finding it for just two?
While the core methods (prime factorization and division) are the same, the key difference lies in the scope. When working with three numbers, you must account for the factors of all three. In the division method, you continue dividing as long as the prime divisor can divide at least one of the numbers in the row. In the prime factorization method, you must identify the highest power of each prime factor across all three numbers, which can be more complex than comparing just two.
6. Why is the LCM of a set of numbers always greater than or equal to the largest number in that set?
By definition, the LCM must be a multiple of every number in the set, including the largest one. A multiple of a number can only be the number itself (when multiplied by 1) or a larger value. Therefore, the LCM must be at least as large as the greatest number in the set to be divisible by it. It can only be equal to the largest number if all the other numbers are its factors.
7. Is there a simple formula connecting the HCF and LCM of three numbers?
No, there is no simple formula like the one for two numbers (Product = HCF × LCM). The relationship for three numbers is more complex and not typically used for calculation. It is much more practical and reliable to find the LCM of three numbers directly using either the prime factorization or the division method as per the NCERT syllabus.
8. How can you use the LCM to solve a problem like finding the smallest number exactly divisible by 12, 15, and 20?
The "smallest number that is exactly divisible by" a set of numbers is simply their LCM. To solve this, you find the LCM of 12, 15, and 20.
- Prime factors of 12 = 2² × 3
- Prime factors of 15 = 3 × 5
- Prime factors of 20 = 2² × 5
9. What is the importance of finding the LCM when adding or subtracting fractions?
The LCM is essential for adding or subtracting fractions that have different denominators. To perform these operations, the fractions must be converted into equivalent fractions with a common denominator. The most efficient common denominator to use is the Least Common Denominator (LCD), which is simply the LCM of the original denominators. This keeps the numbers smaller and simplifies the calculation process.





















