




How to Find the HCF of 150: Method & Application
The greatest available number that splits both integers completely is the Highest Common Factor (HCF) of two numbers. The greatest common factor (HCF) is sometimes known as the greatest common divisor (GCD). HCF can be calculated using the prime factorisation and repeated division methods.
HCF by Prime Factorisation
When two numbers, say p and q, are divided exactly by the biggest available number, the result is known as the highest common factor of the two numbers. When we give the product of two prime numbers, say x and y, we are showing their prime factorization. This indicates that prime factorization is represented by the product of two prime integers. The following are the actions we must take:
Find the prime factorization of the given integers one by one.
Make a list of the numbers' similar prime factors.
The HCF of given numbers is the product of common prime factors.
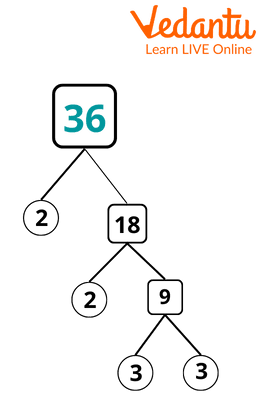
Prime Factorization of 36
Example of HCF By Prime Factorisation
Let's solve some HCF problems to have a better idea.
Let's find out the HCF of 45 and 150 using the prime factorisation method.
First, find the prime factors of 150 and 45 separately.
The similar factors obtained by both of them need to be noted down.
These same numbers are then multiplied to obtain HCF.
Firstly write down what is the factor of 150 and 45. Prime factorisation of 45 will give \[5 \times 3 \times 3 \times 1\] as prime factors. The prime factorisation of 150 will give \[5 \times 5 \times 3 \times 2 \times 1\] as prime factors. Among these prime factors, 3 and 5 are common in both of them. If we multiply 3 and 5 we will get 15 as a result. So, 15 is the HCF of 45 and 150.
HCF by Repeated Division
To get the HCF of two integers using the division method, follow the steps below.
Divide the greater number by the lesser number.
Consider the remainder of the preceding step the divisor, and the divisor of the preceding step the dividend, then repeat the long division.
Continue long division until the remainder equals zero.
When remainder = 0, HCF is the last divisor left.
Example of HCF by Repeated Division
To understand this let's take an example of finding HCF of 56 and 84 using the repeated division method.
Divide 84 by 56. The remainder obtained from this would be 28.
Now we need to divide 56 with the remainder we got in the previous step.
As the remainder now we got is 0. So the HCF obtained is 28.
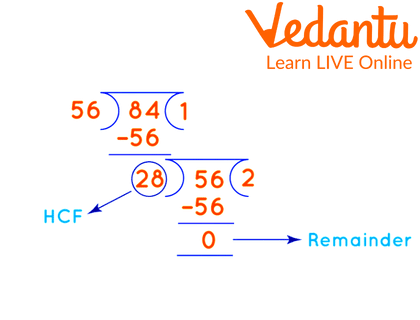
HCF of 56 and 84
Conclusion
The listed factors approach may also be used to calculate the HCF of two integers. In this procedure, we list all the factors of two integers and find the one with the greatest common factor. The HCF of two numbers is always less than or equal to one of them. The HCF between two prime numbers always equals one.
Sample Questions
1. HCF of 20 and 15 is
a. 3
b. 4
c. 5
d. 2
Ans: 5
Explanation: the prime factors of 20 are \[5 \times 2 \times 2 \times 1\] . And the prime factors of 15 are \[5 \times 3 \times 1\] . The factor 5 is common in both numbers. So, the HCF of 15 and 20 is 5.
2. HCF of 150 and 300 is
a. 15
b. 150
c. 5
d. 100
Ans: 150
Explanation: The prime factors of 150 are \[5 \times 5 \times 3 \times 2 \times 1\] . And the prime factors of 300 are \[5 \times 5 \times 3 \times 2 \times 2 \times 1\] . 5, 5, 3, and 2 are common in both numbers making their product result 150. So, the HCF of 150 and 300 is 150.
3. HCF of 12 and 18 is
a. 4
b. 5
c. 6
d. 7
Ans: 6
Explanation: the prime factors of 12 are \[3 \times 2 \times 2 \times 1\] and of 18 are \[3 \times 3 \times 2 \times 1\]. The common factors are 2 and 3 so the hcf of 12 and 18 is 6.
FAQs on HCF of 150 Explained: Steps, Examples & Importance
1. What is the definition of the Highest Common Factor (HCF) in the context of a number like 150?
The Highest Common Factor (HCF) is the largest positive integer that divides two or more numbers without leaving a remainder. For a single number like 150, the concept of HCF is typically used to find its relationship with another number. For example, when finding the HCF of 150 and 225, we look for the biggest number that is a factor of both 150 and 225.
2. How do you find the HCF of 150 and 225 using the prime factorisation method?
To find the HCF of 150 and 225 using prime factorisation, you follow these steps:
- First, break down each number into its prime factors.
- Prime factors of 150: 2 × 3 × 5 × 5
- Prime factors of 225: 3 × 3 × 5 × 5
- Next, identify the prime factors that are common to both lists. In this case, they are one '3' and two '5's.
- Finally, multiply these common prime factors together: 3 × 5 × 5 = 75.
Therefore, the HCF of 150 and 225 is 75.
3. What is an example of finding the HCF of 150 and 300 using the long division method?
The long division method is an efficient way to find the HCF. Here’s how it works for 150 and 300:
- Step 1: Divide the larger number (300) by the smaller number (150).
- Step 2: 300 ÷ 150 = 2, with a remainder of 0.
- Step 3: Since the remainder is 0 in the first step, the divisor (150) is the HCF.
So, the HCF of 150 and 300 is 150.
4. What is the difference between HCF and LCM, using the numbers 150 and 225 as an example?
The main difference lies in what they measure:
- The Highest Common Factor (HCF) is the largest number that can divide both 150 and 225. As calculated, the HCF is 75. It is always less than or equal to the smaller of the two numbers.
- The Lowest Common Multiple (LCM) is the smallest number that is a multiple of both 150 and 225. The LCM of 150 and 225 is 450. It is always greater than or equal to the larger of the two numbers.
In short, HCF is a measure of common divisors, while LCM is a measure of common multiples.
5. In what real-world situations is finding the HCF of numbers like 150 important?
Understanding HCF has several practical applications. For example:
- Simplifying Fractions: To simplify the fraction 150/225, you can divide both the numerator and the denominator by their HCF (75) to get its simplest form, 2/3.
- Organising Groups: If you have 150 red marbles and 225 blue marbles, the HCF (75) tells you the largest number of identical groups you can create, with each group containing 2 red marbles and 3 blue marbles.
- Measurement and Design: In tasks like tiling a floor, HCF helps determine the largest possible square tile size that can cover a rectangular area without any wastage.
6. Can the HCF of 150 and another number be greater than 150? Explain why or why not.
No, the HCF of 150 and any other number cannot be greater than 150. By definition, a 'factor' of a number must divide it completely, meaning it must be less than or equal to the number itself. Since the HCF must be a factor of both numbers, it cannot logically be larger than the smaller of the two numbers involved. The highest possible HCF for a pair including 150 is 150 itself (e.g., HCF of 150 and 300).
7. What is the difference between the 'highest factor' of 150 and the 'Highest Common Factor' (HCF)?
This is a key conceptual distinction:
- The highest factor of a single number is always the number itself. So, the highest factor of 150 is 150.
- The Highest Common Factor (HCF) is a term that applies to a set of two or more numbers. It is the largest factor that is common to all the numbers in the set. For example, the HCF of 150 and 75 is 75. The word 'common' is the critical difference, implying a comparison between multiple numbers.
8. What are all the factors of the number 150?
A factor is any number that divides 150 without leaving a remainder. To find all the factors, you can think of the pairs of numbers that multiply to give 150. The factors of 150 are:
1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, and 150.









