




How to Find HCF Using Long Division-Simple Steps for Students
As we all know, the Highest Common Factor (HCF) as the name itself says, it's the method of finding the highest common factors of two or more than two numbers. It's the highest common number that can divide the given two or more two positive numbers equally.
There are different methods through which we can find out the HCF of given numbers. Of Course, it can be used to find the HCF of small numbers but when it comes to large numbers, then the most suitable method is the Long Division Method. Come on, let us understand HCF by the long division method step by step with a few examples along the way.
What is H.C.F?
HCF stands for Highest Common Factor. HCF of 2 numbers is the highest factor that can divide the two numbers easily. The highest common factor (HCF) can be evaluated for 2 or more than 2 numbers. It is the greatest divisor for any two or more numbers that can equally or completely divide the given numbers.
For Example, the HCF of 60 and 75 is 15 because 15 is the largest number which can divide both 60 and 75 exactly.
Methods for Finding H.C.F
HCF of two or more number can be found by using two methods:
By prime factorization method
By division method
We will discuss the division method in this article.
Steps of HCF by Long Division Method
Step 1: Divide the larger number by the smaller number.
HCF of 18 and 30
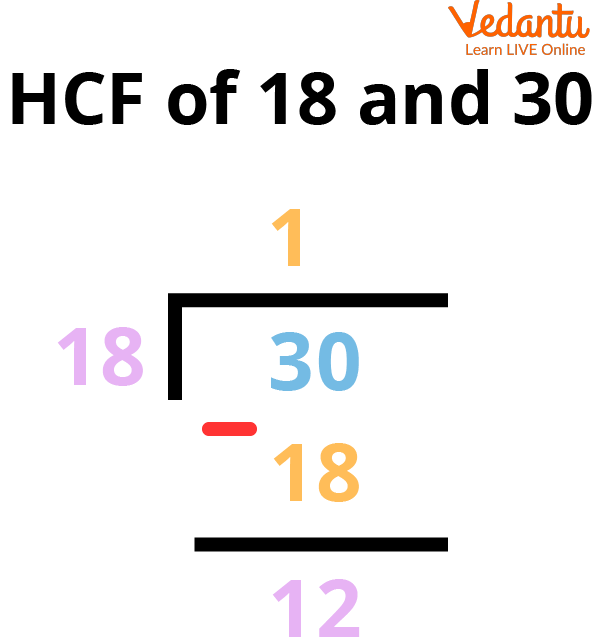
The Long Division Method
Step 2: The remainder becomes the divisor and the divisor becomes the dividend. Therefore, divide the first divisor by the first remainder.
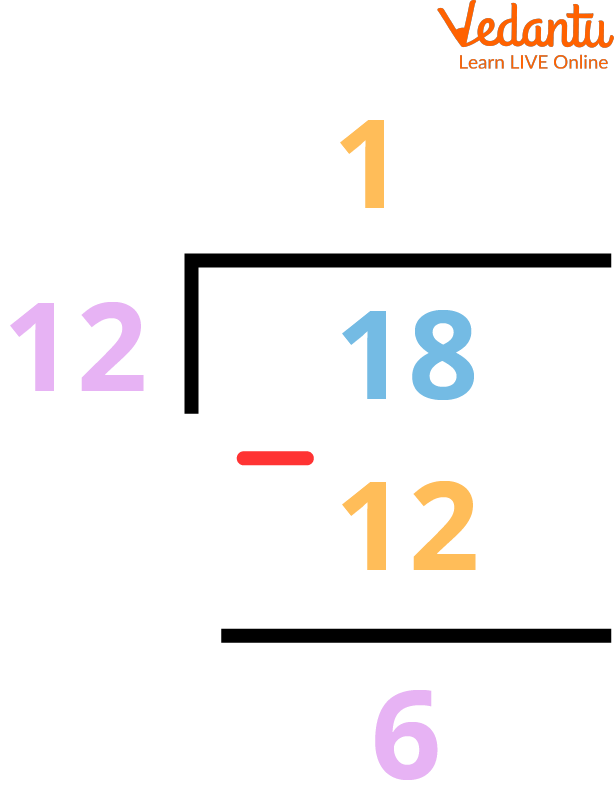
The Long Division Method
Step 3: If the remainder is not 0, then again the remainder becomes the divisor and the divisor becomes the dividend. Therefore, divide the second divisor by the second remainder.
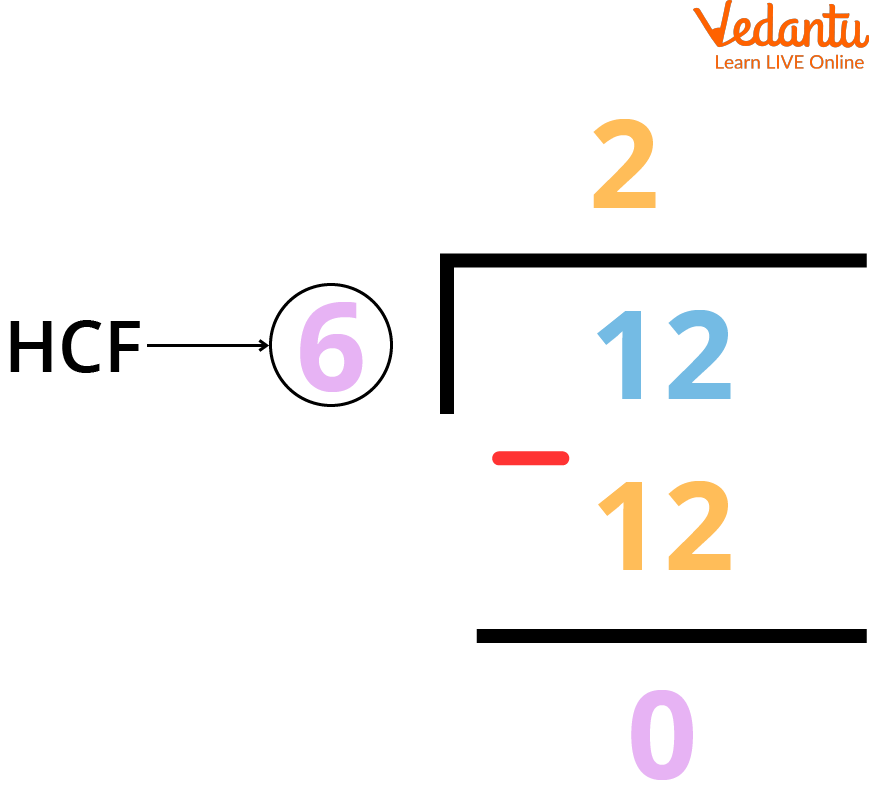
The Long Division Method
Step 4: The divisor which does not leave a remainder is the HCF of the two numbers and thus, the last divisor becomes the HCF of the given two numbers.
Let us try to understand the long division method to find the HCF of given numbers with examples.
Solved Examples
Example 1:Find the HCF of 64 and 144 using the long division method
Step 1: Dividing the larger given number with the smaller given number. So, 144 becomes the dividend and 64 as the divisor.
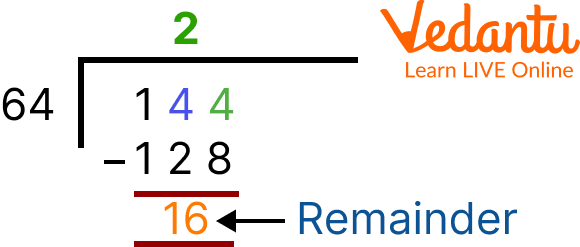
Long Division Method
Step 2: The remainder becomes the divisor and the divisor becomes the dividend.
Step 3: Therefore, we need to divide 64 (dividend) by 16 (divisor).
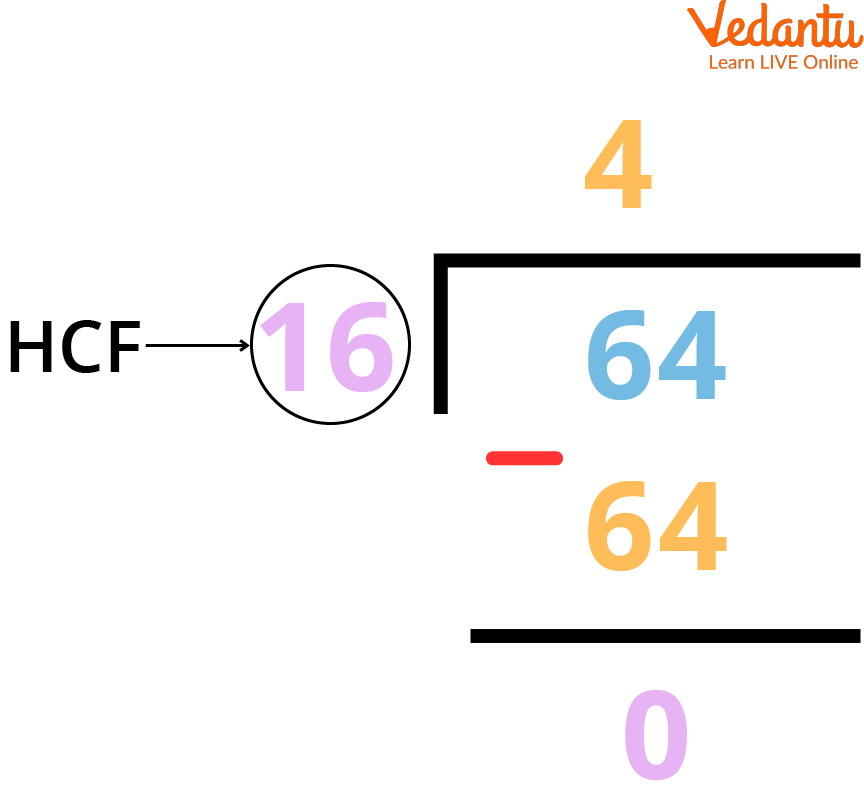
Long Division Method
Once the remainder becomes 0, the divisor of that particular division becomes the HCF.
Therefore, HCF of (64, 144) = 16
Example 2: Find the HCF of 700 and 300 using the long division method.
Step 1: Simply divide the larger given number by the smaller given number. In this case, 300 is the divisor and 700 is the dividend.
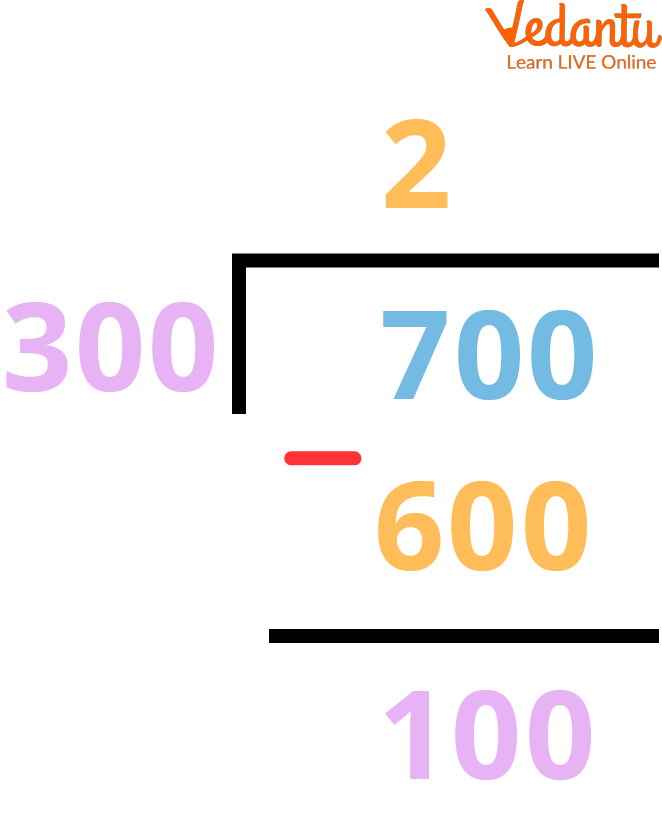
Long Division Method
Step 2: The remainder that we got is 100 therefore the remainder that is 100 becomes the divisor and 300 which was the divisor earlier becomes the dividend.
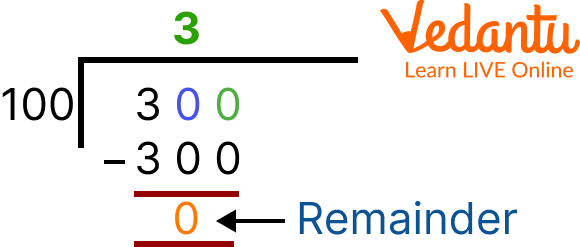
Long Division Method
Step 3: Now, we simply divide the second divisor with the second remainder. Follow the image down below for a better understanding.
=> HCF of 700 and 300 is 100
Practice questions
1. Find the HCF of 30 and 45
Ans: 15
2. Find the HCF of 162 and 180
Ans: 18
3. Find the HCF of 270 and 9
Ans: 9
4. Find the HCF of 78 and 98
Ans: 2
5. Find the HCF of 702 and 405
Ans: 27
Summary
This article has tried to explain the detailed steps of how to find HCF by using the long Division method for 2 positive given numbers. To find the HCF by division method, the first step is to divide the larger number by the smaller number and then the remainder becomes the divisor and divide the smaller number until the remainder is zero. In this article, you have learn about all other different topics related to HCF.
FAQs on HCF by Long Division Method Made Easy
1. What are the steps to find the HCF of two numbers using the long division method?
To find the Highest Common Factor (HCF) using the long division method, you follow these sequential steps:
- Step 1: Divide the larger number (dividend) by the smaller number (divisor).
- Step 2: Check the remainder. If the remainder is 0, the divisor is the HCF.
- Step 3: If the remainder is not 0, make the previous divisor the new dividend and the remainder the new divisor.
- Step 4: Repeat this division process until the remainder becomes 0. The last divisor that gives a remainder of 0 is the HCF of the two numbers.
2. What exactly is HCF, and what are its other names?
HCF stands for Highest Common Factor. It is the largest positive integer that divides two or more given integers without leaving any remainder. It is also commonly known by other names, such as Greatest Common Divisor (GCD) and Greatest Common Measure (GCM). The concept is fundamental in number theory for simplifying fractions and solving various mathematical problems.
3. How is the long division method extended to find the HCF of three or more numbers?
To find the HCF of three numbers (e.g., a, b, and c), the long division method is applied in stages:
- First, find the HCF of any two of the numbers, say 'a' and 'b'. Let's call this result HCF1.
- Next, find the HCF of the third number 'c' and the result from the first step, HCF1.
- The final result of this second HCF calculation is the HCF of all three numbers (a, b, and c). This process can be continued for any number of integers.
4. Why does the last non-zero divisor in the long division method give the HCF?
The long division method for finding HCF is based on Euclid's Division Algorithm. The principle states that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. By repeatedly taking the remainder, we are essentially reducing the numbers until we find a number that divides both the previous divisor and the final dividend perfectly. This final divisor must be the greatest common factor that was shared by the original two numbers.
5. How does the HCF by long division method differ from the prime factorisation method?
Both methods find the HCF, but their approaches are different:
- Prime Factorisation Method: This involves breaking down each number into its prime factors. The HCF is then the product of the lowest powers of all common prime factors. This method is intuitive but can be time-consuming for very large numbers.
- Long Division Method: This is a procedural algorithm that relies on repeated division. It is often more efficient and quicker for large numbers, as it doesn't require finding all the prime factors, which can be a difficult task.
6. Where is the concept of HCF used in real-life applications?
The HCF has several practical, real-world applications. For instance, it can be used to:
- Determine the largest size of square tiles that can pave a rectangular floor without any cutting.
- Split different quantities of items into the largest possible identical groups, with nothing left over.
- Arrange people or objects into the maximum number of rows with an equal number of items or people in each row.
7. Is it possible for the HCF of two numbers to be 1? What are such numbers called?
Yes, the HCF of two numbers can be 1. This occurs when the numbers have no common factors other than 1. Such pairs of numbers are called co-prime or relatively prime numbers. For example, the HCF of 8 and 15 is 1, so they are co-prime. This is a common scenario, especially with consecutive integers.















