




Solved Examples: HCF of Three Numbers Explained
The highest number that completely divides two numbers is known as the Highest Common Factor (HCF). The Greatest Common Divisor (GCD) is another name for the Highest Common Factor (HCF) (GCD). The HCF of two numbers can be determined in a variety of methods. Using the prime factorization method is one of the easiest ways to get the HCF of two or more numbers. In this article, we will learn how to find HCF by long division method with some examples.
Steps to Find HCF of 3 Numbers by Using the Long Division Method
Follow the Steps for a better understanding:
Step 1: We first need to find out the HCF of the first two given numbers.
Step 2: Find out the HCF of the third number given and the HCF of the first two numbers that we got from the previous step.
Step 3: We mark the highest factor among which we found common.
Solved Examples
Q1. Find the HCF of 144, 198 and 162
Ans: Using the long division method
First of all, arrange the given numbers in ascending order. Not necessary but preferable.
Let's first find out the HCF of the first 2 numbers which are 144 and 198. i.e. HCF of 144 and 198.
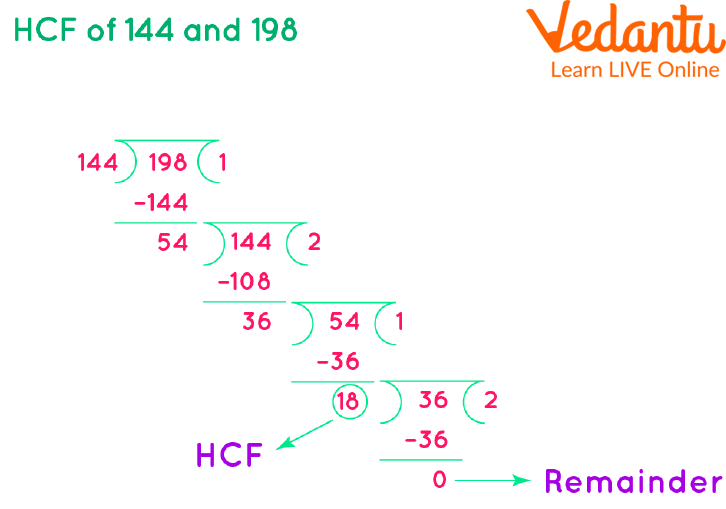
HCF of 144 and 198 by Using Long Division Method
Therfore, the HCF of 144 and 198 = 18
The next step is to find the HCF of 162 and 18

HCF of 162 and 18
So by applying HCF division method, we get HCF of 162 and 18 = 18
Therefore the HCF of all the 3 numbers is
HCF of 144, 198 and 162 = 18
Note: It's Important that the Remainder is Always 0 at the End
Let's try to understand with one more example
Q2. Find the HCF of 729, 864 and 945
Ans: Using the long division method
Let's first find out the HCF of the first 2 numbers which are 729 and 864. i.e. HCF of 864 and 729.
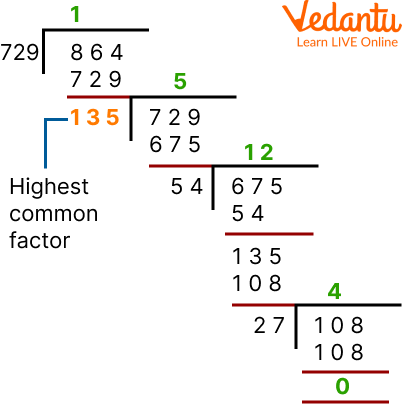
HCF of 864 and 729
The HCF of HCF of 864 and 729 = 27
The next step is to find the HCF of the third number that is given which is 945 and the HCF of the first two numbers which is 27.
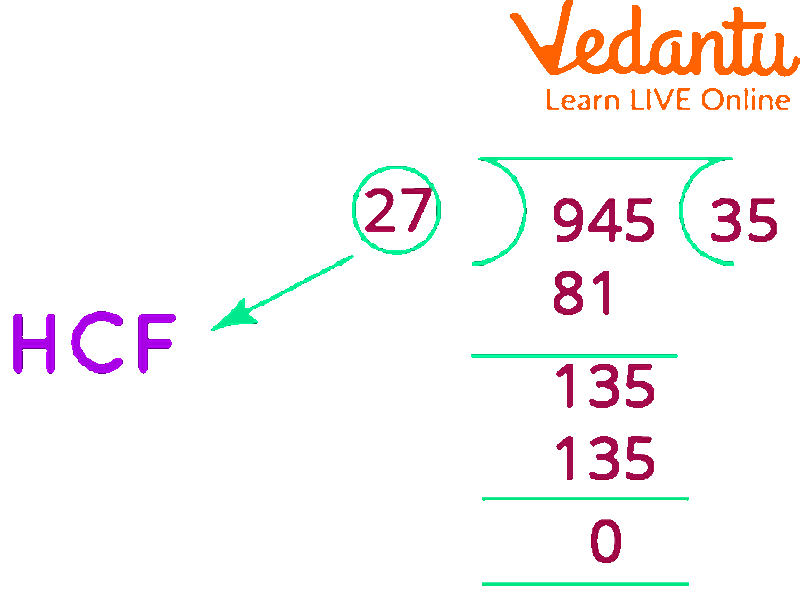
HCF of 945 and 27
HCF of 945 and 27 = 27
Therefore the HCF of all the 3 numbers is 27.
HCF of 729, 864 and 945 = 27
Practice Problem
Q1. Find the HCF of 30, 45 and 150
Ans: 15
Q2. Find the HCF of 126, 162 and 180
Ans: 18
Q3. Find the HCF of 300, 270 and 9
Ans: 3
Q4. Find the HCF of 78, 98 and 108
Ans: 2
Q5. Find the HCF of 702, 153 and 405
Ans: 9
Summary
This article has tried to explain the detailed steps of how to find HCF by using the long Division method for 3 given numbers. To find the HCF by division method the first step is to divide the larger number by the smaller number and then the remainder becomes the divisor and divide the smaller number until the remainder is zero. So, read the whole content nicely and do the solved examples present here in this article.
FAQs on Simple Steps to Find HCF of 3 Numbers
1. What is the HCF of three numbers?
The HCF (Highest Common Factor) of three numbers is the largest positive integer that divides all three numbers without leaving a remainder. It is also known as the Greatest Common Divisor (GCD). For example, the HCF of 12, 18, and 30 is 6, because 6 is the largest number that can divide all three completely.
2. How do you find the HCF of three numbers using the prime factorisation method?
To find the HCF of three numbers using the prime factorisation method, you need to follow these steps:
- First, break down each of the three numbers into its prime factors.
- Next, identify all the prime factors that are common to the factor lists of all three numbers.
- Finally, multiply these common prime factors together. The resulting product is the HCF.
3. What are the steps to find the HCF of three numbers by the long division method?
The long division method for finding the HCF of three numbers is a two-stage process:
- Step 1: Choose any two of the three numbers and find their HCF using the standard division method. To do this, divide the larger number by the smaller one, then the divisor by the remainder, and repeat until the remainder is 0. The last divisor is the HCF of these two numbers.
- Step 2: Now, take the HCF found in Step 1 and the third original number. Find their HCF using the same long division method. The result is the HCF of all three numbers.
4. When is it better to use prime factorisation versus the long division method for three numbers?
The best method depends on the numbers themselves:
- Use prime factorisation when the numbers are small and you can easily identify their factors (e.g., 20, 30, 40). It is more intuitive and helps understand the concept of common factors.
- Use the long division method when the numbers are large or appear to be prime, making them difficult to factorise quickly. This method is more procedural and reliable for complex numbers where finding prime factors would be very time-consuming.
5. Is there a simple formula relating the LCM and HCF for three numbers, like there is for two numbers?
No, the simple product rule for two numbers, which is HCF(a, b) × LCM(a, b) = a × b, does not work for three numbers. The formula HCF(a, b, c) × LCM(a, b, c) = a × b × c is incorrect. The relationship between the HCF and LCM of three numbers is more complex and cannot be simplified into a direct product formula.
6. What are some real-life examples where finding the HCF of three numbers is useful?
Finding the HCF of three numbers has several practical applications:
- Tiling and Cutting: To find the largest possible size of a square tile that can perfectly pave a room with dimensions like 403cm, 434cm, and 465cm, without any wastage.
- Grouping and Distribution: To divide three different sets of items into the largest possible identical groups. For example, creating fruit baskets from 48 apples, 60 oranges, and 72 bananas, so that each basket has the same composition of fruits.
- Measurement: To find the longest measuring tape that can exactly measure three different lengths.
7. How can Euclid's division algorithm be used to find the HCF of three numbers?
To find the HCF of three numbers (let's call them a, b, and c) using Euclid's division algorithm, you must apply the algorithm twice:
- First, apply Euclid's algorithm to any two of the numbers, for example, 'a' and 'b', to find their HCF. Let's name this result 'h'.
- Second, apply the algorithm again to find the HCF of the result 'h' and the third number 'c'.
8. Can the HCF of three positive numbers ever be 1? What about 0?
Yes, the HCF of three numbers can be 1, but it cannot be 0 for positive numbers.
- The HCF is 1 when the three numbers have no common factors other than 1. Such a set of numbers is called 'co-prime'. For instance, the HCF of 8, 9, and 25 is 1.
- The HCF can be 0 only in the special case where all the given numbers are 0, i.e., HCF(0, 0, 0) = 0. For any set containing at least one non-zero number, the HCF will always be a positive integer.
9. What is the key difference between HCF and LCM when dealing with three numbers?
The key difference between HCF and LCM for three numbers lies in what they represent:
- HCF (Highest Common Factor) is the largest number that can divide all three numbers. It will always be a value less than or equal to the smallest of the three given numbers.
- LCM (Lowest Common Multiple) is the smallest number that is a multiple of all three numbers. It will always be a value greater than or equal to the largest of the three given numbers.















