
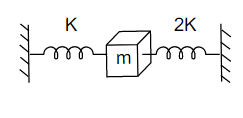
Two springs of force constants K and 2K are connected to a mass as shown below. The frequency of oscillation of the mass is
A. \[\dfrac{1}{{2\pi }}\sqrt {\dfrac{K}{m}} \]
B. \[\dfrac{1}{{2\pi }}\sqrt {\dfrac{{2K}}{m}} \]
C. \[\dfrac{1}{{2\pi }}\sqrt {\dfrac{{3K}}{m}} \]
D. \[\dfrac{1}{{2\pi }}\sqrt {\dfrac{m}{K}} \]
Answer
180k+ views
Hint: Frequency of oscillation directly proportional to the square root of spring constant and in case of combination of springs the effective spring constant for the system is taken under consideration.
Formula used :
\[n = \dfrac{1}{{2\pi }}\sqrt {\dfrac{K}{m}} \]
Here, n = Frequency of oscillation, K = Spring constant and m = Mass
Complete step by step solution:
Frequency of oscillation is defined as the number of oscillation that took place in a unit of time i.e. second and is mathematically given by the formula,
\[n = \dfrac{1}{{2\pi }}\sqrt {\dfrac{K}{m}} \]
Where, Here, n = Frequency of oscillation, K = Spring constant and m = Mass
For the given spring mass system spring constant of individual spring is K and 2K respectively and the frequency of oscillation the system will be,
\[n = \dfrac{1}{{2\pi }}\sqrt {\dfrac{{{K_{eff}}}}{m}} \,\]
Where,\[{K_{eff}} = \]Effective constant of the system.
Effective constant for the given system of springs constant K and 2K will be the sum of both constants.
\[{K_{eff}} = K + 2K\, = 3K\]
So the frequency of oscillation of the system will be,
\[n = \dfrac{1}{{2\pi }}\sqrt {\dfrac{{3K}}{m}} \,\]
Therefore, option C is the correct answer.
Note: When two or more springs are connected end to end then they are said to be in series combination and in parallel combination springs are connected side by side.
Formula used :
\[n = \dfrac{1}{{2\pi }}\sqrt {\dfrac{K}{m}} \]
Here, n = Frequency of oscillation, K = Spring constant and m = Mass
Complete step by step solution:
Frequency of oscillation is defined as the number of oscillation that took place in a unit of time i.e. second and is mathematically given by the formula,
\[n = \dfrac{1}{{2\pi }}\sqrt {\dfrac{K}{m}} \]
Where, Here, n = Frequency of oscillation, K = Spring constant and m = Mass
For the given spring mass system spring constant of individual spring is K and 2K respectively and the frequency of oscillation the system will be,
\[n = \dfrac{1}{{2\pi }}\sqrt {\dfrac{{{K_{eff}}}}{m}} \,\]
Where,\[{K_{eff}} = \]Effective constant of the system.
Effective constant for the given system of springs constant K and 2K will be the sum of both constants.
\[{K_{eff}} = K + 2K\, = 3K\]
So the frequency of oscillation of the system will be,
\[n = \dfrac{1}{{2\pi }}\sqrt {\dfrac{{3K}}{m}} \,\]
Therefore, option C is the correct answer.
Note: When two or more springs are connected end to end then they are said to be in series combination and in parallel combination springs are connected side by side.
Recently Updated Pages
Uniform Acceleration - Definition, Equation, Examples, and FAQs

JEE Atomic Structure and Chemical Bonding important Concepts and Tips

JEE Amino Acids and Peptides Important Concepts and Tips for Exam Preparation

JEE Electricity and Magnetism Important Concepts and Tips for Exam Preparation

Chemical Properties of Hydrogen - Important Concepts for JEE Exam Preparation

JEE Energetics Important Concepts and Tips for Exam Preparation

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Displacement-Time Graph and Velocity-Time Graph for JEE

Atomic Structure - Electrons, Protons, Neutrons and Atomic Models

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

What is Hybridisation in Chemistry?

Other Pages
NCERT Solutions For Class 11 Physics Chapter 2 Motion In A Straight Line - 2025-26

NCERT Solutions For Class 11 Physics Chapter 1 Units and Measurements - 2025-26

NCERT Solutions For Class 11 Physics Chapter 3 Motion In A Plane - 2025-26

JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26

Motion in a Straight Line Class 11 Physics Chapter 2 CBSE Notes - 2025-26




