
Two similar bar Magnets $P$ and $Q$ each of magnetic moment $M$ are taken. If $P$ is cut along its axial line and $Q$ along its equatorial line all the four pieces obtained have each of
A. Equal pole strength
B. Magnetic Moment $\dfrac{M}{4}$
C. Magnetic Moment $\dfrac{M}{2}$
D. Magnetic Moment $M$
Answer
174k+ views
Hint:
When a bar magnet is cut into two equal halves, each tiny magnet behaves like a magnet and has both the north and south pole. It is found that the magnetic field due to a tiny bar magnet at any point along its axial line is twice the magnetic field at a point along the equatorial line with the same distance.
Formula used:
The formula used to solve this question is given as follows: -
Magnetic dipole moment, $M = ml$
Complete step by step solution:
Initially, the magnetic moment of $P$ and $Q$ is $M$ (given)
We know that $M = ml$ is the magnetic dipole moment of a bar magnet.
Where m = pole strength and l = length of a bar magnet
Now, for magnet $P$, when it is cut along its axial line length remains the same but pole strength becomes halved as: -
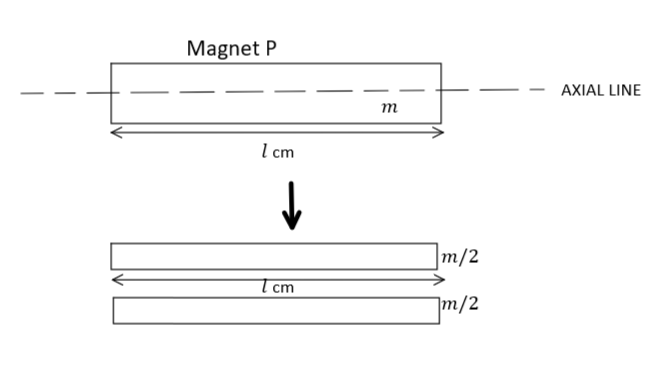
Therefore, in this case, magnetic moment will be: ${M_P} = \left( {\dfrac{m}{2}} \right)l = \dfrac{{ml}}{2} = \dfrac{M}{2}$ $\left( {\therefore M = ml} \right)$
Now, for magnet $Q$, when it is cut along its equatorial line pole strength remains the same but length becomes halved as: -
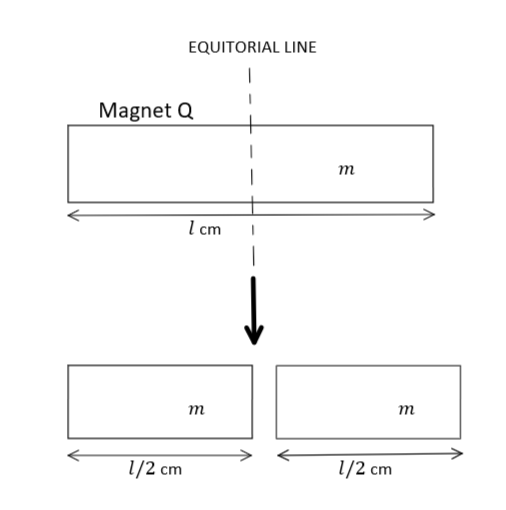
Therefore, in this case, magnetic moment will be: ${M_Q} = m\left( {\dfrac{l}{2}} \right) = \dfrac{{ml}}{2} = \dfrac{M}{2}$
Thus, when the two magnets $P$ and $Q$ is cut according to the question, the resulting magnetic moment of both the magnets will become ${M_P} = {M_Q} = \dfrac{M}{2}$.
Hence, the correct option is (C) Magnetic Moment $\dfrac{M}{2}$.
Therefore, the correct option is C.
Note:
Since this is a problem related to a uniform magnetic field and magnetic dipole moment hence, we should always remember that the direction of magnetic field is the same direction as that of magnetic dipole moment vector due to tiny bar magnet.
When a bar magnet is cut into two equal halves, each tiny magnet behaves like a magnet and has both the north and south pole. It is found that the magnetic field due to a tiny bar magnet at any point along its axial line is twice the magnetic field at a point along the equatorial line with the same distance.
Formula used:
The formula used to solve this question is given as follows: -
Magnetic dipole moment, $M = ml$
Complete step by step solution:
Initially, the magnetic moment of $P$ and $Q$ is $M$ (given)
We know that $M = ml$ is the magnetic dipole moment of a bar magnet.
Where m = pole strength and l = length of a bar magnet
Now, for magnet $P$, when it is cut along its axial line length remains the same but pole strength becomes halved as: -

Therefore, in this case, magnetic moment will be: ${M_P} = \left( {\dfrac{m}{2}} \right)l = \dfrac{{ml}}{2} = \dfrac{M}{2}$ $\left( {\therefore M = ml} \right)$
Now, for magnet $Q$, when it is cut along its equatorial line pole strength remains the same but length becomes halved as: -

Therefore, in this case, magnetic moment will be: ${M_Q} = m\left( {\dfrac{l}{2}} \right) = \dfrac{{ml}}{2} = \dfrac{M}{2}$
Thus, when the two magnets $P$ and $Q$ is cut according to the question, the resulting magnetic moment of both the magnets will become ${M_P} = {M_Q} = \dfrac{M}{2}$.
Hence, the correct option is (C) Magnetic Moment $\dfrac{M}{2}$.
Therefore, the correct option is C.
Note:
Since this is a problem related to a uniform magnetic field and magnetic dipole moment hence, we should always remember that the direction of magnetic field is the same direction as that of magnetic dipole moment vector due to tiny bar magnet.
Recently Updated Pages
JEE Main 2025-26 Atoms and Nuclei Mock Test: Free Practice Online

JEE Main 2025-26: Dual Nature of Matter and Radiation Mock Test

JEE Main 2025-26 Electronic Devices Mock Test – Free Practice

JEE Main Mock Test 2025-26: Experimental Skills Chapter Online Practice

JEE Main 2025-26 Current Electricity Mock Test: Free Practice Online

JEE Main 2025-26 Rotational Motion Mock Test – Free Practice Online

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

Displacement-Time Graph and Velocity-Time Graph for JEE

Uniform Acceleration

Electric field due to uniformly charged sphere class 12 physics JEE_Main

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Instantaneous Velocity - Formula based Examples for JEE

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

Essential Derivations for CBSE Class 12 Physics: Stepwise & PDF Solutions

Electron Gain Enthalpy and Electron Affinity for JEE

What is Hybridisation in Chemistry?




