
Two points charges 4q and –q are fixed on the x-axis at x = \[ - \left( {\dfrac{d}{2}} \right)\] and x =\[\left( {\dfrac{d}{2}} \right)\] , respectively. If a third point charge ‘q’ is taken from the origin to x = d along the semicircle as shown in the figure, the energy of the charge will:
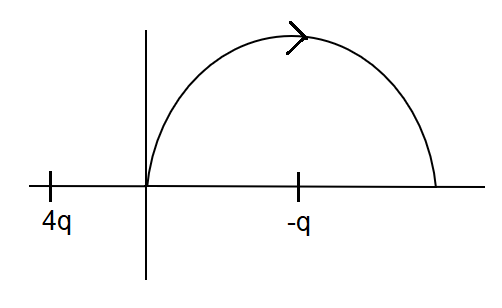
A. decrease by \[\dfrac{q^2}{{4\pi {\varepsilon _0}d}}\]
B. decrease by \[\dfrac{{4q^2}}{{3\pi {\varepsilon _0}d}}\]
C. increase by \[\dfrac{{3q^2}}{{4\pi {\varepsilon _0}d}}\]
D. increase by \[\dfrac{{2{q^2}}}{{3\pi {\varepsilon _0}d}}\]
Answer
156.6k+ views
Hint: To solve this question first we need to find initial potential energy and final potential energy. After subtracting the both we get the change in potential energy. Electric potential energy is defined as the energy that is required to move a charge opposite to the electric field.
Formula used:
The potential energy is given as,
\[U = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{q}{r}\]
Where q is the charge, r is the distance and \[{\varepsilon _0}\] is the permittivity.
Complete step by step solution:
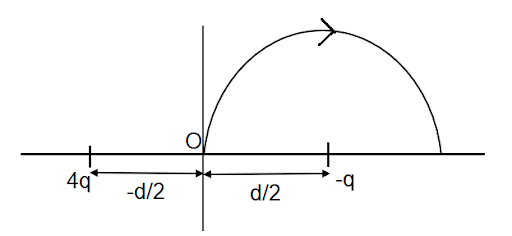
Image: Two point charges 4q and –q are at a distance of \[ - \left( {\dfrac{d}{2}} \right)\] and \[\left( {\dfrac{d}{2}} \right)\] on the x-axis with respect to origin.
As we know the initial potential energy is given as,
\[{U_i} = \dfrac{1}{{4\pi {\varepsilon _0}}}\left[ {\dfrac{{4{q^2}}}{{\left( {\dfrac{d}{2}} \right)}} - \dfrac{{{q^2}}}{{\left( {\dfrac{d}{2}} \right)}}} \right]\]
As the final potential energy is given as,
\[{U_f} = \dfrac{1}{{4\pi {\varepsilon _0}}}\left[ {\dfrac{{4{q^2}}}{{\left( {\dfrac{{3d}}{2}} \right)}} - \dfrac{{{q^2}}}{{\left( {\dfrac{d}{2}} \right)}}} \right]\]
Now the change in potential energy will be
\[\Delta U = {U_f} - {U_i}\]
\[\Rightarrow \Delta U =\dfrac{1}{{4\pi {\varepsilon _0}}}\left[ {\dfrac{{4{q^2}}}{{\left( {\dfrac{{3d}}{2}} \right)}} - \dfrac{{{q^2}}}{{\left( {\dfrac{d}{2}} \right)}}} \right]\]-\[\dfrac{1}{{4\pi {\varepsilon _0}}}\left[ {\dfrac{{4{q^2}}}{{\left( {\dfrac{d}{2}} \right)}} - \dfrac{{{q^2}}}{{\left( {\dfrac{d}{2}} \right)}}} \right]\]
\[\therefore \Delta U = - \dfrac{{4{q^2}}}{{3\pi {\varepsilon _0}d}}\]
Here the negative sign shows the decreasing energy. Therefore, the energy of the charge will decrease by \[\dfrac{{4{q^2}}}{{3\pi {\varepsilon _0}d}}\].
Hence option B is the correct answer.
Note: As we know the energy that is needed to move a charge against an electric field. We need greater energy to accelerate a charge in the electric field but also greater energy to move it through a stronger electric field. At any given point in an electric field the electric potential energy is the electric potential multiplied by the amount of charge at that point. So, the voltage gives you how much potential energy could have at some point which is not dependent on how much charge you put there.
Formula used:
The potential energy is given as,
\[U = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{q}{r}\]
Where q is the charge, r is the distance and \[{\varepsilon _0}\] is the permittivity.
Complete step by step solution:

Image: Two point charges 4q and –q are at a distance of \[ - \left( {\dfrac{d}{2}} \right)\] and \[\left( {\dfrac{d}{2}} \right)\] on the x-axis with respect to origin.
As we know the initial potential energy is given as,
\[{U_i} = \dfrac{1}{{4\pi {\varepsilon _0}}}\left[ {\dfrac{{4{q^2}}}{{\left( {\dfrac{d}{2}} \right)}} - \dfrac{{{q^2}}}{{\left( {\dfrac{d}{2}} \right)}}} \right]\]
As the final potential energy is given as,
\[{U_f} = \dfrac{1}{{4\pi {\varepsilon _0}}}\left[ {\dfrac{{4{q^2}}}{{\left( {\dfrac{{3d}}{2}} \right)}} - \dfrac{{{q^2}}}{{\left( {\dfrac{d}{2}} \right)}}} \right]\]
Now the change in potential energy will be
\[\Delta U = {U_f} - {U_i}\]
\[\Rightarrow \Delta U =\dfrac{1}{{4\pi {\varepsilon _0}}}\left[ {\dfrac{{4{q^2}}}{{\left( {\dfrac{{3d}}{2}} \right)}} - \dfrac{{{q^2}}}{{\left( {\dfrac{d}{2}} \right)}}} \right]\]-\[\dfrac{1}{{4\pi {\varepsilon _0}}}\left[ {\dfrac{{4{q^2}}}{{\left( {\dfrac{d}{2}} \right)}} - \dfrac{{{q^2}}}{{\left( {\dfrac{d}{2}} \right)}}} \right]\]
\[\therefore \Delta U = - \dfrac{{4{q^2}}}{{3\pi {\varepsilon _0}d}}\]
Here the negative sign shows the decreasing energy. Therefore, the energy of the charge will decrease by \[\dfrac{{4{q^2}}}{{3\pi {\varepsilon _0}d}}\].
Hence option B is the correct answer.
Note: As we know the energy that is needed to move a charge against an electric field. We need greater energy to accelerate a charge in the electric field but also greater energy to move it through a stronger electric field. At any given point in an electric field the electric potential energy is the electric potential multiplied by the amount of charge at that point. So, the voltage gives you how much potential energy could have at some point which is not dependent on how much charge you put there.
Recently Updated Pages
JEE Atomic Structure and Chemical Bonding important Concepts and Tips

JEE Amino Acids and Peptides Important Concepts and Tips for Exam Preparation

Wheatstone Bridge - Working Principle, Formula, Derivation, Application

Young's Double Slit Experiment Step by Step Derivation

JEE Electricity and Magnetism Important Concepts and Tips for Exam Preparation

Chemical Properties of Hydrogen - Important Concepts for JEE Exam Preparation

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Electric Field Due to Uniformly Charged Ring for JEE Main 2025 - Formula and Derivation

Electric field due to uniformly charged sphere class 12 physics JEE_Main

Degree of Dissociation and Its Formula With Solved Example for JEE

Displacement-Time Graph and Velocity-Time Graph for JEE

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

JEE Advanced 2025 Notes

Geostationary Satellites and Geosynchronous Satellites - JEE Important Topic

Electrical Field of Charged Spherical Shell - JEE

Formula for number of images formed by two plane mirrors class 12 physics JEE_Main




