
Two identical cylindrical vessels, with their bases at the same level, each contain a liquid of density $\rho $. The height in one vessel is ${h_1}$ and that in the other is ${h_2}$. The area of either base is A. What is the work done by gravity in equalising the levels when the vessels are interconnected:
A) $A\rho g{\left( {\dfrac{{{h_1} - {h_2}}}{2}} \right)^2}$.
B) $A\rho g{\left( {\dfrac{{{h_1} + {h_2}}}{2}} \right)^2}$.
C) $\dfrac{1}{2}A\rho g{\left( {{h_1} - {h_2}} \right)^2}$.
D) $\text{None of these.}$
Answer
118.5k+ views
Hint: The work done is defined as the energy required as to move an object for some distance. The product of applied force and distance is known as work done and it is represented in terms of joules. Density is defined as the ratio of mass and volume.
Formula used: The formula of work done is given by,
$ \Rightarrow W = mgh$
Where mass is m, the height is h and the acceleration due to gravity is g.
Complete step by step solution:
It is given in the problem that two identical cylindrical vessels, with their bases at the same level, each contain a liquid of density $\rho $ the height in one vessel in ${h_1}$ and that in the other is ${h_2}$ the area of either base is A we need to find the work done by gravity in equalising the levels when the vessels are interconnected and we need to select the correct answer for this problem.
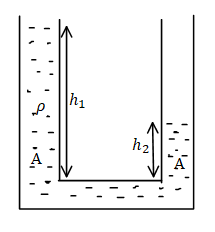
Let the height h be equal to,
$ \Rightarrow h = \dfrac{{{h_1} + {h_2}}}{2}$
The decrease in height in the vessel of height${h_1}$.
$ \Rightarrow \Delta h = {h_1} - \left( {\dfrac{{{h_1} + {h_2}}}{2}} \right)$
$ \Rightarrow \Delta h = \left( {\dfrac{{{h_1} - {h_2}}}{2}} \right)$
Mass of the liquid is equal to,
$ \Rightarrow m = \left( {\dfrac{{{h_1} - {h_2}}}{2}} \right)\rho A$
The formula of work done is given by,
$ \Rightarrow W = mgh$
Where mass is m, the height is h and the acceleration due to gravity is g.
$ \Rightarrow W = mgh$
$ \Rightarrow W = \left( {\dfrac{{{h_1} - {h_2}}}{2}} \right) \times \rho A \times g \times \left( {\dfrac{{{h_1} - {h_2}}}{2}} \right)$
$ \Rightarrow W = {\left( {\dfrac{{{h_1} - {h_2}}}{2}} \right)^2}A\rho g$
The work done is equal to $W = {\left( {\dfrac{{{h_1} - {h_2}}}{2}} \right)^2}A\rho g$.
The correct answer for this problem is option A.
Note: The students are advised to understand and remember the formula of the work done as it is very useful in solving these kinds of problems. Whenever two columns are attached and they are having the same liquid with different levels then they come to the same level as the liquid flows from high pressure to low pressure and it stops when the liquid levels.
Formula used: The formula of work done is given by,
$ \Rightarrow W = mgh$
Where mass is m, the height is h and the acceleration due to gravity is g.
Complete step by step solution:
It is given in the problem that two identical cylindrical vessels, with their bases at the same level, each contain a liquid of density $\rho $ the height in one vessel in ${h_1}$ and that in the other is ${h_2}$ the area of either base is A we need to find the work done by gravity in equalising the levels when the vessels are interconnected and we need to select the correct answer for this problem.

Let the height h be equal to,
$ \Rightarrow h = \dfrac{{{h_1} + {h_2}}}{2}$
The decrease in height in the vessel of height${h_1}$.
$ \Rightarrow \Delta h = {h_1} - \left( {\dfrac{{{h_1} + {h_2}}}{2}} \right)$
$ \Rightarrow \Delta h = \left( {\dfrac{{{h_1} - {h_2}}}{2}} \right)$
Mass of the liquid is equal to,
$ \Rightarrow m = \left( {\dfrac{{{h_1} - {h_2}}}{2}} \right)\rho A$
The formula of work done is given by,
$ \Rightarrow W = mgh$
Where mass is m, the height is h and the acceleration due to gravity is g.
$ \Rightarrow W = mgh$
$ \Rightarrow W = \left( {\dfrac{{{h_1} - {h_2}}}{2}} \right) \times \rho A \times g \times \left( {\dfrac{{{h_1} - {h_2}}}{2}} \right)$
$ \Rightarrow W = {\left( {\dfrac{{{h_1} - {h_2}}}{2}} \right)^2}A\rho g$
The work done is equal to $W = {\left( {\dfrac{{{h_1} - {h_2}}}{2}} \right)^2}A\rho g$.
The correct answer for this problem is option A.
Note: The students are advised to understand and remember the formula of the work done as it is very useful in solving these kinds of problems. Whenever two columns are attached and they are having the same liquid with different levels then they come to the same level as the liquid flows from high pressure to low pressure and it stops when the liquid levels.
Recently Updated Pages
Geostationary Satellites and Geosynchronous Satellites for JEE

Complex Numbers - Important Concepts and Tips for JEE

JEE Main 2023 (February 1st Shift 2) Maths Question Paper with Answer Key

JEE Main 2022 (July 25th Shift 2) Physics Question Paper with Answer Key

Inertial and Non-Inertial Frame of Reference for JEE

Hinge Force - Important Concepts and Tips for JEE

Trending doubts
Free Radical Substitution Mechanism of Alkanes for JEE Main 2025

Electron Gain Enthalpy and Electron Affinity for JEE

Collision - Important Concepts and Tips for JEE

JEE Main Chemistry Exam Pattern 2025

The diagram given shows how the net interaction force class 11 physics JEE_Main

An Lshaped glass tube is just immersed in flowing water class 11 physics JEE_Main

Other Pages
NCERT Solutions for Class 11 Physics Chapter 4 Laws of Motion

NCERT Solutions for Class 11 Physics Chapter 3 Motion In A Plane

NCERT Solutions for Class 11 Physics Chapter 13 Oscillations

Find the current in wire AB class 11 physics JEE_Main

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Keys & Solutions

Thermodynamics Class 11 Notes CBSE Physics Chapter 11 (Free PDF Download)




