Question

An L-shaped glass tube is just immersed in flowing water such that its opening is pointing against flowing water. If the speed of water current is v, then :


A. The water in the tube rises to height \[\dfrac{{{v^2}}}{{2g}}\]
B. The water in the tube rises to height \[\dfrac{g}{{2{v^2}}}\]
C. The water in the tube does not rise at all.
D. None of these.

Answer 1

Hint:When the pressure is equal then fluid does not flow as the fluid flows in the direction of the higher pressure to the lower pressure. The fluid in the tube is at rest. So the pressure inside the tube should be equal.

Formula used:
\[P = \rho gh\]
where P is the pressure due to fluid density \[\rho \] and h is the height of the fluid, g is the acceleration due to gravity.

Complete step by step solution:

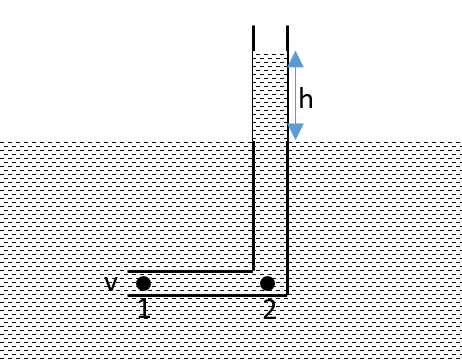
Image: The L-shaped tube inside the flowing water

We take two points, point 1 outside the tube and point 2 inside the tube but on the same horizontal level. The water at point 1 is flowing at the speed of v and the water at point 2 is at rest.
\[{v_1} = v\]
\[\Rightarrow {v_2} = 0\]

Let the pressure at point 1 is \[{P_1}\]and the pressure at point 2 is \[{P_2}\]. The pressure at point 1 is due to the water level and at the same horizontal level the pressure must be the same. For point 2, the height of the water is h. So, the pressure at point 2 is the sum of the pressure at point 1 and the pressure due to water of height h.
\[{P_2} = {P_1} + \rho gh\]
The density of the water is \[\rho \].

Applying Bernoulli’s equation between the two considered points 1 and 2, we get
\[{P_1} + \dfrac{{\rho v_1^2}}{2} + \rho g{h_1} = {P_2} + \dfrac{{\rho v_2^2}}{2} + \rho g{h_2} \\ \]
\[\Rightarrow {P_1} + \dfrac{{\rho v_1^2}}{2} + \rho g{h_1} = \left( {{P_1} + \rho gh} \right) + \dfrac{{\rho v_2^2}}{2} + \rho g{h_2}\]

As two points are on the same horizontal line, \[{h_1} = {h_2}\]
\[\dfrac{{\rho {v^2}}}{2} + \rho g{h_1} = \rho gh + \dfrac{{\rho {{\left( 0 \right)}^2}}}{2} + \rho g{h_1} \\ \]
On simplifying, we get
\[\dfrac{{\rho {v^2}}}{2} = \rho gh \\ \]
\[\therefore h = \dfrac{{{v^2}}}{{2g}}\]

Therefore, the correct option is A.

Note: We must be careful when choosing two points to apply Bernoulli's theorem. One point should be outside the tube and the other should be inside the tube. If we take both the points inside the tube then there will be variation of pressure and due to which the fluid in the tube will start flowing and the height of the fluid in the tube will not be static.