
Find the current in wire AB
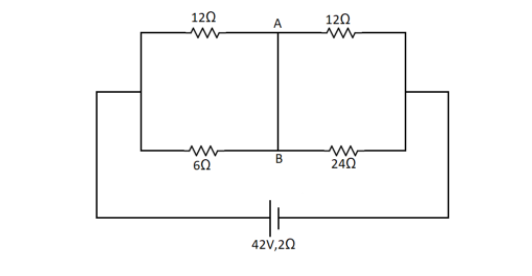
Answer
219.6k+ views
Hint: The wire AB in between connects all the 4 resistances. So by drawing the circuit in a simpler way, we can find the equivalent resistance. Then we can calculate the current being drawn from the cell using the emf of the call. This will be the current in the wire AB.
Formula Used In this solution, we are going to use the following formula,
${R_{eq}} = {R_1} + {R_2} + {R_3} + ....$ where ${R_{eq}}$ is the equivalent resistance when the resistances are placed in series.
And $\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} + ....$ where ${R_{eq}}$ is the equivalent resistance when the resistances are placed in a parallel circuit.
$V = IR$ where $V$ is the emf of the cell, $I$ is the current in the wires and $R$ is the equivalent resistance.
Complete Step by Step Solution
To find the current in the wire AB we need to first redraw the circuit in a more simple way. Here the points A and B are the same point joined by a wire. So we can draw the circuit as,
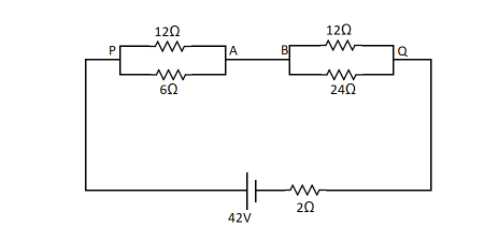
From this circuit we can see that there are 2 parallel circuits consisting of 2 resistances each.
Let us first find the equivalent resistance between the points P and Q. The formula for parallel combination is
$\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} + ....$
Here we have ${R_1} = 12\Omega $ and ${R_2} = 6\Omega $
So substituting we get,
$\dfrac{1}{{{R_{eq1}}}} = \dfrac{1}{{12}} + \dfrac{1}{6}$
Taking LCM as 12
$\dfrac{1}{{{R_{eq1}}}} = \dfrac{{1 + 2}}{{12}}$
So by taking the reciprocal we get,
${R_{eq1}} = \dfrac{{12}}{3} = 4\Omega $
Similarly, between the points B and Q we have 2 resistances in parallel combination. So again here ${R_1} = 12\Omega $ and ${R_2} = 24\Omega $
Substituting we get,
$\dfrac{1}{{{R_{eq2}}}} = \dfrac{1}{{12}} + \dfrac{1}{{24}}$
Taking LCM as 24,
$\dfrac{1}{{{R_{eq2}}}} = \dfrac{{2 + 1}}{{24}}$
Taking the reciprocal we get,
${R_{eq2}} = \dfrac{{24}}{3} = 8\Omega $
Now the resistance ${R_{eq1}}$, ${R_{eq2}}$ and the internal resistance of the battery are in series in the circuit. So we use the formula for series combination given by,
${R_{eq}} = {R_1} + {R_2} + {R_3} + ....$
Here ${R_1} = {R_{eq1}} = 4\Omega $, ${R_2} = {R_{eq2}} = 8\Omega $ and ${R_3} = 2\Omega $
So we get,
${R_{eq}} = 4 + 8 + 2$
Therefore, we get the equivalent resistance as,
${R_{eq}} = 14\Omega $
Now it is given that the battery has an emf of $V = 42V$
So from the Ohm’s law $V = IR$, we can get the current as,
$I = \dfrac{V}{{{\operatorname{R} _{eq}}}}$
Substituting we get,
$I = \dfrac{{42}}{{14}} = 3A$
This is the whole current that is in the flowing through the wire. Now since between the points A and B the current doesn’t get divided, so the current in the wire AB will be $3A$.
Note: In the given circuit, when the two resistances are in series condition then the current that flows in them both is the same whereas when the resistances are in parallel, the potential difference is the same across the resistances but the current varies. So the current in the 2 wires between P and A are different and depends on the magnitude of the resistance.
Formula Used In this solution, we are going to use the following formula,
${R_{eq}} = {R_1} + {R_2} + {R_3} + ....$ where ${R_{eq}}$ is the equivalent resistance when the resistances are placed in series.
And $\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} + ....$ where ${R_{eq}}$ is the equivalent resistance when the resistances are placed in a parallel circuit.
$V = IR$ where $V$ is the emf of the cell, $I$ is the current in the wires and $R$ is the equivalent resistance.
Complete Step by Step Solution
To find the current in the wire AB we need to first redraw the circuit in a more simple way. Here the points A and B are the same point joined by a wire. So we can draw the circuit as,

From this circuit we can see that there are 2 parallel circuits consisting of 2 resistances each.
Let us first find the equivalent resistance between the points P and Q. The formula for parallel combination is
$\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} + ....$
Here we have ${R_1} = 12\Omega $ and ${R_2} = 6\Omega $
So substituting we get,
$\dfrac{1}{{{R_{eq1}}}} = \dfrac{1}{{12}} + \dfrac{1}{6}$
Taking LCM as 12
$\dfrac{1}{{{R_{eq1}}}} = \dfrac{{1 + 2}}{{12}}$
So by taking the reciprocal we get,
${R_{eq1}} = \dfrac{{12}}{3} = 4\Omega $
Similarly, between the points B and Q we have 2 resistances in parallel combination. So again here ${R_1} = 12\Omega $ and ${R_2} = 24\Omega $
Substituting we get,
$\dfrac{1}{{{R_{eq2}}}} = \dfrac{1}{{12}} + \dfrac{1}{{24}}$
Taking LCM as 24,
$\dfrac{1}{{{R_{eq2}}}} = \dfrac{{2 + 1}}{{24}}$
Taking the reciprocal we get,
${R_{eq2}} = \dfrac{{24}}{3} = 8\Omega $
Now the resistance ${R_{eq1}}$, ${R_{eq2}}$ and the internal resistance of the battery are in series in the circuit. So we use the formula for series combination given by,
${R_{eq}} = {R_1} + {R_2} + {R_3} + ....$
Here ${R_1} = {R_{eq1}} = 4\Omega $, ${R_2} = {R_{eq2}} = 8\Omega $ and ${R_3} = 2\Omega $
So we get,
${R_{eq}} = 4 + 8 + 2$
Therefore, we get the equivalent resistance as,
${R_{eq}} = 14\Omega $
Now it is given that the battery has an emf of $V = 42V$
So from the Ohm’s law $V = IR$, we can get the current as,
$I = \dfrac{V}{{{\operatorname{R} _{eq}}}}$
Substituting we get,
$I = \dfrac{{42}}{{14}} = 3A$
This is the whole current that is in the flowing through the wire. Now since between the points A and B the current doesn’t get divided, so the current in the wire AB will be $3A$.
Note: In the given circuit, when the two resistances are in series condition then the current that flows in them both is the same whereas when the resistances are in parallel, the potential difference is the same across the resistances but the current varies. So the current in the 2 wires between P and A are different and depends on the magnitude of the resistance.
Recently Updated Pages
Electricity and Magnetism Explained: Key Concepts & Applications

JEE Energetics Important Concepts and Tips for Exam Preparation

JEE Isolation, Preparation and Properties of Non-metals Important Concepts and Tips for Exam Preparation

JEE Main 2021 July 25 Shift 1 Question Paper with Answer Key

JEE Main 2021 July 22 Shift 2 Question Paper with Answer Key

States of Matter Chapter For JEE Main Chemistry

Trending doubts
Understanding Uniform Acceleration in Physics

Understanding Atomic Structure for Beginners

Understanding Centrifugal Force in Physics

JEE Main Marking Scheme 2026- Paper-Wise Marks Distribution and Negative Marking Details

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Understanding Average and RMS Value in Electrical Circuits

Other Pages
NCERT Solutions for Class 11 Physics Chapter 6 System Of Particles And Rotational Motion 2025-26

Understanding Entropy Changes in Different Processes

Common Ion Effect: Concept, Applications, and Problem-Solving

Understanding Excess Pressure Inside a Liquid Drop

NCERT Solutions For Class 11 Physics Chapter 12 Kinetic Theory - 2025-26

Motion In A Plane Class 11 Physics Chapter 3 CBSE Notes - 2025-26




