
The solar constant for the earth is S. The surface temperature of the sun is \[{T_{}}K\]. The sun subtends an angle \[\theta \] at the earth
(A) \[S \propto {T^4}\]
(B) \[S \propto {T^2}\]
(C) \[S \propto {\theta ^2}\]
(D) \[S \propto \theta \]
Answer
199.5k+ views
Hint Let R be the distance between the center of earth and the surface of the sun and let \[{R_e}\]be the radius of the earth. Now, use the energy received per unit area on earth’s surface formula to find the relation.
Complete Step By Step Solution
Let us draw the given scenario in a simple diagram. The sun rays hit the earth across its center and tangent points. Let R be the distance between the surface of the sun and the centre of the earth. Now, \[{R_e}\] is the radius of the earth. The sun rays subtend an angle \[\theta \], with respect to R. The image is shown below:
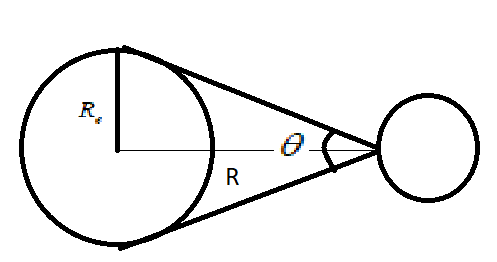
Now, Solar energy received per unit area is defined as the amount of solar energy received over the earth’s surface from the sun. Solar constant is defined as the ratio between the power received from the sun and the square of the distance between sun and center of the earth. Mathematically, given as
\[S = \dfrac{P}{{4\pi {R^2}}}\]
Power radiated by the sun is mathematically given as
\[P = {A_s} \times \sigma {T^4}\], where A is area of the sun, T is temperature on the surface of the sun and \[\sigma \] is Stefan-Boltzmann constant
Substituting P on the above formula we get,
\[ \Rightarrow S = \dfrac{{4\pi {R_s}^2 \times \sigma {T^4}}}{{4\pi {R^2}}}\]
Cancelling out the common terms, we get,
\[ \Rightarrow S = \dfrac{{{R_s}^2 \times \sigma {T^4}}}{{{R^2}}}\]
\[ \Rightarrow S \propto {T^4}\]
Thus, Option (A) is the correct answer for the given question.
Note The power radiated by the sun is defined as the product of power density of the sun’s rays and the total surface area of the sun. Since the sun is a star, the Stefan-Boltzmann law applies, which describes the power radiated by a black body with respect to its temperature.
Complete Step By Step Solution
Let us draw the given scenario in a simple diagram. The sun rays hit the earth across its center and tangent points. Let R be the distance between the surface of the sun and the centre of the earth. Now, \[{R_e}\] is the radius of the earth. The sun rays subtend an angle \[\theta \], with respect to R. The image is shown below:

Now, Solar energy received per unit area is defined as the amount of solar energy received over the earth’s surface from the sun. Solar constant is defined as the ratio between the power received from the sun and the square of the distance between sun and center of the earth. Mathematically, given as
\[S = \dfrac{P}{{4\pi {R^2}}}\]
Power radiated by the sun is mathematically given as
\[P = {A_s} \times \sigma {T^4}\], where A is area of the sun, T is temperature on the surface of the sun and \[\sigma \] is Stefan-Boltzmann constant
Substituting P on the above formula we get,
\[ \Rightarrow S = \dfrac{{4\pi {R_s}^2 \times \sigma {T^4}}}{{4\pi {R^2}}}\]
Cancelling out the common terms, we get,
\[ \Rightarrow S = \dfrac{{{R_s}^2 \times \sigma {T^4}}}{{{R^2}}}\]
\[ \Rightarrow S \propto {T^4}\]
Thus, Option (A) is the correct answer for the given question.
Note The power radiated by the sun is defined as the product of power density of the sun’s rays and the total surface area of the sun. Since the sun is a star, the Stefan-Boltzmann law applies, which describes the power radiated by a black body with respect to its temperature.
Recently Updated Pages
Chemical Equation - Important Concepts and Tips for JEE

JEE Main 2022 (July 29th Shift 1) Chemistry Question Paper with Answer Key

Conduction, Transfer of Energy Important Concepts and Tips for JEE

JEE Analytical Method of Vector Addition Important Concepts and Tips

Atomic Size - Important Concepts and Tips for JEE

JEE Main 2022 (June 29th Shift 1) Maths Question Paper with Answer Key

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

Equation of Trajectory in Projectile Motion: Derivation & Proof

Atomic Structure: Definition, Models, and Examples

How to Convert a Galvanometer into an Ammeter or Voltmeter

Hybridisation in Chemistry – Concept, Types & Applications

Angle of Deviation in a Prism – Formula, Diagram & Applications

Other Pages
Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26

Motion in a Straight Line Class 11 Physics Chapter 2 CBSE Notes - 2025-26

JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Motion In A Plane Class 11 Physics Chapter 3 CBSE Notes - 2025-26

NCERT Solutions For Class 11 Physics Chapter 1 Units and Measurements - 2025-26

NCERT Solutions for Class 11 Physics Chapter 3 Motion In A Plane 2025-26




