
The rate of change of charge \[Q\], in Coulombs retained by a capacitor. \[t\] minutes after charging is given by $\dfrac{{dQ}}{{dt}} = - ak{e^{kt}}$. Using the graph shown, determine the charge remaining after.
A) \[{\text{One hour}}\]
B) \[80{\text{ minutes}}\]
Answer
174.3k+ views
Hint: The rate of change of the charge is represented in terms of time in exponential form. Find the charge by integration. Put the value of charge at time zero from the graph and from it find the value of integration constant and also the constant term $k$ .
The equation of charge and time put the value of times given in the problem and calculate the charges respectively.
Complete step by step answer:
The rate of change of charge s given in terms of time, $\dfrac{{dQ}}{{dt}} = - ak{e^{kt}}$
By integration we get,
$Q = - ak\dfrac{{{e^{kt}}}}{k} + c$
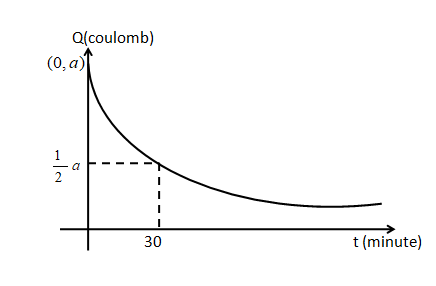
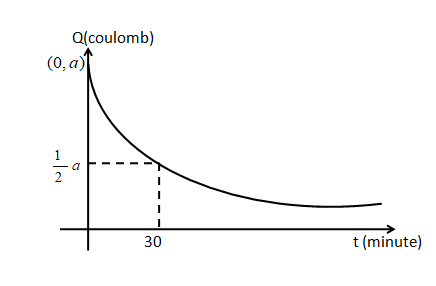
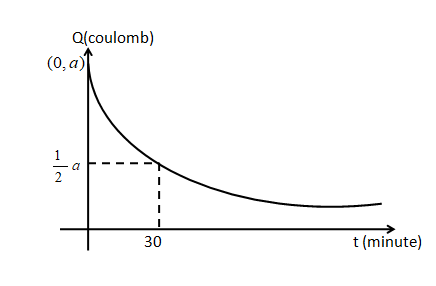
The graph shown below is the relation between the charge and the time. The charge \[Q\] is in the coulomb unit and the time \[t\] is in a minute.
To get the equation of the charge we have to integrate by separation of variables method, as follows
$\int {dQ} = - ak\int {{e^{kt}}dt} + c$ where, $c$ is the integrating constant.
$ \Rightarrow Q = - ak\dfrac{{{e^{kt}}}}{k} + c$
$ \Rightarrow Q = - a{e^{kt}} + c$…………….(1)
Now from the graph, we get, at $t = 0,{\text{ }}Q = a$
So, from eq. (1)
$ \Rightarrow a = - a{e^0} + c$
$ \Rightarrow a = - a \times 1 + c$
$ \Rightarrow c = 2a$
Hence the eq. (1) $ \Rightarrow Q = - a{e^{kt}} + 2a$ ……………..(2) [ putting the value of $c$]
From the graph, it is shown that, at $t = 30,{\text{ }}Q = \dfrac{a}{2}$
So, the eq.(2) $ \Rightarrow \dfrac{a}{2} = - a{e^{30k}} + 2a$
$ \Rightarrow a{e^{30k}} = 2a - \dfrac{a}{2}$
On taking LCM we get,
$ \Rightarrow a{e^{30k}} = \dfrac{{3a}}{2}$
On cancelling the term we get,
$ \Rightarrow {e^{30k}} = \dfrac{3}{2}$
Taking $\ln $ both sides of the above equation,
$ \Rightarrow 30k = \ln \dfrac{3}{2}$
Let us divide \[30\] on both sides we get,
$ \Rightarrow k = \dfrac{1}{{30}}\ln \dfrac{3}{2}$ .
Putting the value of $k$ in eq. (2) we get,
$ \Rightarrow Q = - a{e^{\dfrac{t}{{30}}\ln \dfrac{3}{2}}} + 2a$ ……….(3)
Now we have to calculate the charge at time $(a){\text{ }}1{\text{ hour}}$ and $(b){\text{ 80 minutes}}$
$(A) \Rightarrow 1{\text{ hour}} = 60{\text{ minutes}}$
So, eq.(3) $ \Rightarrow Q\left| {_{t = 60}} \right. = - a{e^{\dfrac{{60}}{{30}}\ln \dfrac{3}{2}}} + 2a$
$ \Rightarrow Q\left| {_{t = 60}} \right. = - a{e^{2\ln \dfrac{3}{2}}} + 2a$
$ \Rightarrow Q\left| {_{t = 60}} \right. = - a{e^{\ln {{\left( {\dfrac{3}{2}} \right)}^2}}} + 2a$
On squaring the term and we get
$ \Rightarrow Q\left| {_{t = 60}} \right. = - a{e^{\ln \dfrac{9}{4}}} + 2a$
On canceling the exponents and logarithm we get,
$ \Rightarrow Q\left| {_{t = 60}} \right. = - \dfrac{{9a}}{4} + 2a$
Taking LCM we get
$ \Rightarrow Q\left| {_{t = 60}} \right. = \dfrac{{8a - 9a}}{4}$
Let us subtract the numerator term we get,
$ \Rightarrow Q\left| {_{t = 60}} \right. = - \dfrac{a}{4}$
$(B) \Rightarrow 80{\text{ minutes}}$
So, eq.(3) $ \Rightarrow Q\left| {_{t = 80}} \right. = - a{e^{\dfrac{{80}}{{30}}\ln \dfrac{3}{2}}} + 2a$
\[ \Rightarrow Q\left| {_{t = 80}} \right. = - a{e^{2.66\ln \left( {\dfrac{3}{2}} \right)}} + 2a\]
\[ \Rightarrow Q\left| {_{t = 80}} \right. = - a{e^{\ln 2.94}} + 2a\]
[since, ${\left( {\dfrac{3}{2}} \right)^{2.66}} = 2.94$ ]
\[ \Rightarrow Q\left| {_{t = 80}} \right. = - 2.94a + 2a\]
On subtracting we get,
\[ \Rightarrow Q\left| {_{t = 80}} \right. = - 0.94a\].
Hence the answers for,
$(A){\text{ }} \Rightarrow Q\left| {_{t = 60}} \right. = - \dfrac{a}{4}$and $(B) \Rightarrow Q\left| {_{t = 80}} \right. = - 0.94a$.
Additional information:
If a capacitor is connected to a battery, then the charges are gathered in that capacitor. This is known as the charging of the capacitor. When the batteries are disconnected from the capacitor, the capacitor loses charges. This is called the discharging of the capacitor.
Note: The rate of change of the charge is given, $\dfrac{{dQ}}{{dt}} = - ak{e^{kt}}$
Here the negative sign implies that the charge decreases with the increase of time.
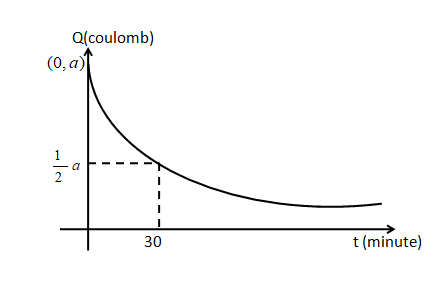
From the graph, we see that the charge decays exponentially. It takes infinite time to be fully discharged.
The equation of charge and time put the value of times given in the problem and calculate the charges respectively.
Complete step by step answer:
The rate of change of charge s given in terms of time, $\dfrac{{dQ}}{{dt}} = - ak{e^{kt}}$
By integration we get,
$Q = - ak\dfrac{{{e^{kt}}}}{k} + c$
The graph shown below is the relation between the charge and the time. The charge \[Q\] is in the coulomb unit and the time \[t\] is in a minute.

To get the equation of the charge we have to integrate by separation of variables method, as follows
$\int {dQ} = - ak\int {{e^{kt}}dt} + c$ where, $c$ is the integrating constant.
$ \Rightarrow Q = - ak\dfrac{{{e^{kt}}}}{k} + c$
$ \Rightarrow Q = - a{e^{kt}} + c$…………….(1)
Now from the graph, we get, at $t = 0,{\text{ }}Q = a$

So, from eq. (1)
$ \Rightarrow a = - a{e^0} + c$
$ \Rightarrow a = - a \times 1 + c$
$ \Rightarrow c = 2a$
Hence the eq. (1) $ \Rightarrow Q = - a{e^{kt}} + 2a$ ……………..(2) [ putting the value of $c$]
From the graph, it is shown that, at $t = 30,{\text{ }}Q = \dfrac{a}{2}$
So, the eq.(2) $ \Rightarrow \dfrac{a}{2} = - a{e^{30k}} + 2a$
$ \Rightarrow a{e^{30k}} = 2a - \dfrac{a}{2}$
On taking LCM we get,
$ \Rightarrow a{e^{30k}} = \dfrac{{3a}}{2}$
On cancelling the term we get,
$ \Rightarrow {e^{30k}} = \dfrac{3}{2}$
Taking $\ln $ both sides of the above equation,
$ \Rightarrow 30k = \ln \dfrac{3}{2}$
Let us divide \[30\] on both sides we get,
$ \Rightarrow k = \dfrac{1}{{30}}\ln \dfrac{3}{2}$ .
Putting the value of $k$ in eq. (2) we get,
$ \Rightarrow Q = - a{e^{\dfrac{t}{{30}}\ln \dfrac{3}{2}}} + 2a$ ……….(3)
Now we have to calculate the charge at time $(a){\text{ }}1{\text{ hour}}$ and $(b){\text{ 80 minutes}}$
$(A) \Rightarrow 1{\text{ hour}} = 60{\text{ minutes}}$
So, eq.(3) $ \Rightarrow Q\left| {_{t = 60}} \right. = - a{e^{\dfrac{{60}}{{30}}\ln \dfrac{3}{2}}} + 2a$
$ \Rightarrow Q\left| {_{t = 60}} \right. = - a{e^{2\ln \dfrac{3}{2}}} + 2a$
$ \Rightarrow Q\left| {_{t = 60}} \right. = - a{e^{\ln {{\left( {\dfrac{3}{2}} \right)}^2}}} + 2a$
On squaring the term and we get
$ \Rightarrow Q\left| {_{t = 60}} \right. = - a{e^{\ln \dfrac{9}{4}}} + 2a$
On canceling the exponents and logarithm we get,
$ \Rightarrow Q\left| {_{t = 60}} \right. = - \dfrac{{9a}}{4} + 2a$
Taking LCM we get
$ \Rightarrow Q\left| {_{t = 60}} \right. = \dfrac{{8a - 9a}}{4}$
Let us subtract the numerator term we get,
$ \Rightarrow Q\left| {_{t = 60}} \right. = - \dfrac{a}{4}$
$(B) \Rightarrow 80{\text{ minutes}}$
So, eq.(3) $ \Rightarrow Q\left| {_{t = 80}} \right. = - a{e^{\dfrac{{80}}{{30}}\ln \dfrac{3}{2}}} + 2a$
\[ \Rightarrow Q\left| {_{t = 80}} \right. = - a{e^{2.66\ln \left( {\dfrac{3}{2}} \right)}} + 2a\]
\[ \Rightarrow Q\left| {_{t = 80}} \right. = - a{e^{\ln 2.94}} + 2a\]
[since, ${\left( {\dfrac{3}{2}} \right)^{2.66}} = 2.94$ ]
\[ \Rightarrow Q\left| {_{t = 80}} \right. = - 2.94a + 2a\]
On subtracting we get,
\[ \Rightarrow Q\left| {_{t = 80}} \right. = - 0.94a\].
Hence the answers for,
$(A){\text{ }} \Rightarrow Q\left| {_{t = 60}} \right. = - \dfrac{a}{4}$and $(B) \Rightarrow Q\left| {_{t = 80}} \right. = - 0.94a$.
Additional information:
If a capacitor is connected to a battery, then the charges are gathered in that capacitor. This is known as the charging of the capacitor. When the batteries are disconnected from the capacitor, the capacitor loses charges. This is called the discharging of the capacitor.
Note: The rate of change of the charge is given, $\dfrac{{dQ}}{{dt}} = - ak{e^{kt}}$
Here the negative sign implies that the charge decreases with the increase of time.

From the graph, we see that the charge decays exponentially. It takes infinite time to be fully discharged.
Recently Updated Pages
JEE Main 2025-26 Atoms and Nuclei Mock Test: Free Practice Online

JEE Main 2025-26: Dual Nature of Matter and Radiation Mock Test

JEE Main 2025-26 Electronic Devices Mock Test – Free Practice

JEE Main Mock Test 2025-26: Experimental Skills Chapter Online Practice

JEE Main 2025-26 Current Electricity Mock Test: Free Practice Online

JEE Main 2025-26 Rotational Motion Mock Test – Free Practice Online

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

Displacement-Time Graph and Velocity-Time Graph for JEE

Uniform Acceleration

Electric field due to uniformly charged sphere class 12 physics JEE_Main

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Instantaneous Velocity - Formula based Examples for JEE

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

Essential Derivations for CBSE Class 12 Physics: Stepwise & PDF Solutions

Electron Gain Enthalpy and Electron Affinity for JEE

What is Hybridisation in Chemistry?




