
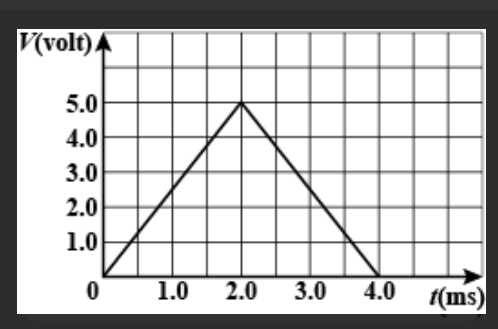
The potential difference across a $150 \mathrm{mH}$ inductor as a function of time is shown in figure. Assume that the initial value of the current in the inductor is zero. What is the current when $t=4.0 \mathrm{ms} ?$
(A) $2.67 \times 10^{-4} \mathrm{A}$
(B) $3.67 \times 10^{-2} \mathrm{A}$
(C) $6.67 \times 10^{-2} \mathrm{A}$
(D) $9.67 \times 10^{-4} \mathrm{A}$
Answer
118.5k+ views
Hint: The electric potential difference between points A and B, VB−VA, is defined to be the change in potential energy of a charge q moved from A to B, divided by the charge. Units of potential difference are joules per coulomb, given the name volt (V) after Alessandro Volta. When a voltage is connected across a wire, an electric field is produced in the wire. Metal wire is a conductor. Some electrons around the metal atoms are free to move from atom to atom. This causes a difference in energy across the component, which is known as an electrical potential difference.
Complete step by step answer
If the electric potential difference between two locations is 1 volt, then one Coulomb of charge will gain 1 joule of potential energy when moved between those two locations. Because electric potential difference is expressed in units of volts, it is sometimes referred to as the voltage.
$\mathrm{V}_{\mathrm{L}}=\mathrm{L} \dfrac{\mathrm{d}}{\mathrm{dt}}$
$\therefore \quad \mathrm{di}=\dfrac{1}{\mathrm{L}}\left(\mathrm{V}_{\mathrm{L}} \mathrm{dt}\right)$
$\therefore \quad \int \mathrm{di}=\mathrm{i}=\dfrac{1}{\mathrm{L}} \int \mathrm{V}_{\mathrm{L}} \mathrm{dt} \quad$ or $\quad \mathrm{i}=\dfrac{1}{\mathrm{L}}$
At $\mathrm{t}=4 \mathrm{ms}$
$\mathrm{i}=\left(150 \times 10^{-3}\right)^{-1}\left(\dfrac{1}{2} \times 4 \times 10^{-3} \times 5\right)=6.67 \times 10^{-2} \mathrm{A}$
So the correct answer is option C.
Note: One volt is defined as the difference in electric potential between two points of a conducting wire when an electric current of one ampere dissipates one watt of power between those points. Voltage, also sometimes called potential difference or electromotive force (EMF), refers to the amount of potential energy the electrons have in an object or circuit. In some ways, you can think of this as the amount of "push" the electrons are making to try to get towards a positive charge. This process defines the electric potential of a point-like charge. Therefore, a system consisting of a negative and a positive point-like charge has a negative potential energy.
Complete step by step answer
If the electric potential difference between two locations is 1 volt, then one Coulomb of charge will gain 1 joule of potential energy when moved between those two locations. Because electric potential difference is expressed in units of volts, it is sometimes referred to as the voltage.
$\mathrm{V}_{\mathrm{L}}=\mathrm{L} \dfrac{\mathrm{d}}{\mathrm{dt}}$
$\therefore \quad \mathrm{di}=\dfrac{1}{\mathrm{L}}\left(\mathrm{V}_{\mathrm{L}} \mathrm{dt}\right)$
$\therefore \quad \int \mathrm{di}=\mathrm{i}=\dfrac{1}{\mathrm{L}} \int \mathrm{V}_{\mathrm{L}} \mathrm{dt} \quad$ or $\quad \mathrm{i}=\dfrac{1}{\mathrm{L}}$
At $\mathrm{t}=4 \mathrm{ms}$
$\mathrm{i}=\left(150 \times 10^{-3}\right)^{-1}\left(\dfrac{1}{2} \times 4 \times 10^{-3} \times 5\right)=6.67 \times 10^{-2} \mathrm{A}$
So the correct answer is option C.
Note: One volt is defined as the difference in electric potential between two points of a conducting wire when an electric current of one ampere dissipates one watt of power between those points. Voltage, also sometimes called potential difference or electromotive force (EMF), refers to the amount of potential energy the electrons have in an object or circuit. In some ways, you can think of this as the amount of "push" the electrons are making to try to get towards a positive charge. This process defines the electric potential of a point-like charge. Therefore, a system consisting of a negative and a positive point-like charge has a negative potential energy.
Recently Updated Pages
JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

Geostationary Satellites and Geosynchronous Satellites for JEE

Complex Numbers - Important Concepts and Tips for JEE

JEE Main 2023 (February 1st Shift 2) Maths Question Paper with Answer Key

JEE Main 2022 (July 25th Shift 2) Physics Question Paper with Answer Key

Inertial and Non-Inertial Frame of Reference for JEE

Trending doubts
JEE Main 2025: Application Form (Out), Exam Dates (Released), Eligibility & More

JEE Main Login 2045: Step-by-Step Instructions and Details

JEE Main Chemistry Question Paper with Answer Keys and Solutions

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

JEE Main 2025: Conversion of Galvanometer Into Ammeter And Voltmeter in Physics

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Dual Nature of Radiation and Matter Class 12 Notes CBSE Physics Chapter 11 (Free PDF Download)

Electric field due to uniformly charged sphere class 12 physics JEE_Main

Degree of Dissociation and Its Formula With Solved Example for JEE

Diffraction of Light - Young’s Single Slit Experiment

JEE Main 2025: Derivation of Equation of Trajectory in Physics




