
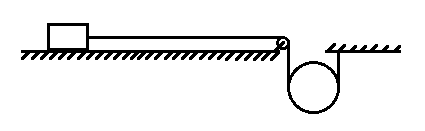
The descending pulley shown in figure has a radius $20cm$ and moment of inertia $0.20kg{m^2}$. The fixed pulley is light and horizontal plane frictionless. Find the acceleration of the block if its mass is $1.0kg$.
Answer
179.7k+ views
Hint: Understand the forces acting on the block and the movable pulley and the directions of all these forces. To find out the value of acceleration, equate these forces as per the direction of the forces.
Complete step by step solution:
In the figure, there are two pulleys, light pulley A & descending pulley B.
Descending pulley B have radius $20cm$ and moment of inertia $0.20kg{m^2}$
Mass of the block is $1.0kg$ as shown in the figure.
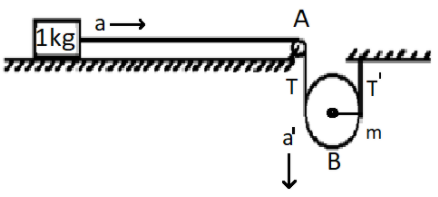
The acceleration of the block=$a$
The acceleration of the descending pulley =$a'$
Tension acting on the left side of the movable pulley= tension acting on the block= $T$
Tension acting on the right side of the movable pulley= $T'$
Mass of the movable pulley= $m$
From the figure we can understand that, the acceleration of the block= double the acceleration of the descending pulley’
That is, $a = 2a'$
$ \Rightarrow a' = \dfrac{a}{2}$………………… (1)
When we consider the block only,
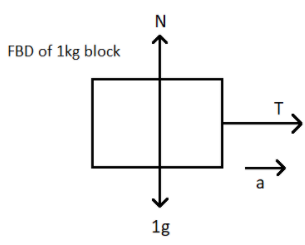
The forces acting on the block are: Gravitational force, normal force, tension, and also there is an acceleration in the direction of the string that is also present.
That is, $T = a$ ………….. (2)
When we consider the movable pulley only,
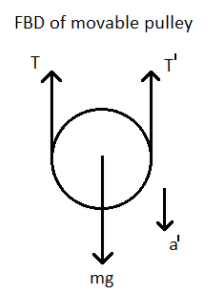
The forces acting on the movable pulley are: Gravitational force, tension on the right side, tension on the left side and also there is an acceleration in downward direction is also present.
That is, $mg - T - T' = ma'$…………………….. (3)
The torque acting will be about the centre of the movable pulley will be,
$\tau = (T' - T) \times R = I \times \alpha $……………….. (4)
Here $\alpha $ is the angular acceleration and the value given by,
$\alpha = \dfrac{{a'}}{R} = \dfrac{a}{{2R}}$
The value of $I$ is given by,
$I = \dfrac{{m{R^2}}}{2}$
Applying these values to the equation (4) we get,
$\tau = (T' - T) \times R = \dfrac{{m{R^2}}}{2} \times \dfrac{a}{{2R}}$
$ \Rightarrow $$ \Rightarrow (T' - T) = \dfrac{m}{4}a$………………….. (5)
It given in the question that, moment of inertia $0.20kg{m^2}$
That is, $I = \dfrac{{m{R^2}}}{2} = 0.2$
From this equation we get,
$m = \dfrac{{0.2 \times 2}}{{{{(0.2)}^2}}}$
$ \Rightarrow m = 10kg$
Applying this value in the equation (5) we get,
$ \Rightarrow (T' - T) = \dfrac{m}{4}a$
$ \Rightarrow (T' - T) = \dfrac{{10}}{4}a = \dfrac{5}{2}a$
$ \Rightarrow T' = \dfrac{5}{2}a + a = \dfrac{7}{2}a$
Applying values in equation (3)
$mg - T - T' = ma'$
$ \Rightarrow (10 \times 9.8) - a - \dfrac{{7a}}{2} = \dfrac{{10a}}{2}$
$ \Rightarrow 98 - \dfrac{{9a}}{2} = 5a$
$ \therefore a = 10.316m{s^{ - 2}}$
Final answer is, the acceleration of the block, $a = 10.316m{s^{ - 2}}$.
Note: A pulley is a wheel on an axle or shaft that is designed to support movement and change of direction of a taut cable or belt, or transfer of power between the shaft and cable or belt. The movable pulley reduces the effort required to pull a mass by factor of $2 \times $ number of movable pulleys.
Complete step by step solution:
In the figure, there are two pulleys, light pulley A & descending pulley B.
Descending pulley B have radius $20cm$ and moment of inertia $0.20kg{m^2}$
Mass of the block is $1.0kg$ as shown in the figure.

The acceleration of the block=$a$
The acceleration of the descending pulley =$a'$
Tension acting on the left side of the movable pulley= tension acting on the block= $T$
Tension acting on the right side of the movable pulley= $T'$
Mass of the movable pulley= $m$
From the figure we can understand that, the acceleration of the block= double the acceleration of the descending pulley’
That is, $a = 2a'$
$ \Rightarrow a' = \dfrac{a}{2}$………………… (1)
When we consider the block only,

The forces acting on the block are: Gravitational force, normal force, tension, and also there is an acceleration in the direction of the string that is also present.
That is, $T = a$ ………….. (2)
When we consider the movable pulley only,

The forces acting on the movable pulley are: Gravitational force, tension on the right side, tension on the left side and also there is an acceleration in downward direction is also present.
That is, $mg - T - T' = ma'$…………………….. (3)
The torque acting will be about the centre of the movable pulley will be,
$\tau = (T' - T) \times R = I \times \alpha $……………….. (4)
Here $\alpha $ is the angular acceleration and the value given by,
$\alpha = \dfrac{{a'}}{R} = \dfrac{a}{{2R}}$
The value of $I$ is given by,
$I = \dfrac{{m{R^2}}}{2}$
Applying these values to the equation (4) we get,
$\tau = (T' - T) \times R = \dfrac{{m{R^2}}}{2} \times \dfrac{a}{{2R}}$
$ \Rightarrow $$ \Rightarrow (T' - T) = \dfrac{m}{4}a$………………….. (5)
It given in the question that, moment of inertia $0.20kg{m^2}$
That is, $I = \dfrac{{m{R^2}}}{2} = 0.2$
From this equation we get,
$m = \dfrac{{0.2 \times 2}}{{{{(0.2)}^2}}}$
$ \Rightarrow m = 10kg$
Applying this value in the equation (5) we get,
$ \Rightarrow (T' - T) = \dfrac{m}{4}a$
$ \Rightarrow (T' - T) = \dfrac{{10}}{4}a = \dfrac{5}{2}a$
$ \Rightarrow T' = \dfrac{5}{2}a + a = \dfrac{7}{2}a$
Applying values in equation (3)
$mg - T - T' = ma'$
$ \Rightarrow (10 \times 9.8) - a - \dfrac{{7a}}{2} = \dfrac{{10a}}{2}$
$ \Rightarrow 98 - \dfrac{{9a}}{2} = 5a$
$ \therefore a = 10.316m{s^{ - 2}}$
Final answer is, the acceleration of the block, $a = 10.316m{s^{ - 2}}$.
Note: A pulley is a wheel on an axle or shaft that is designed to support movement and change of direction of a taut cable or belt, or transfer of power between the shaft and cable or belt. The movable pulley reduces the effort required to pull a mass by factor of $2 \times $ number of movable pulleys.
Recently Updated Pages
JEE Main 2023 (January 29th Shift 1) Maths Question Paper with Answer Key

JEE Main 2023 (January 25th Shift 1) Maths Question Paper with Answer Key

JEE Main 2023 (February 1st Shift 2) Maths Question Paper with Answer Key

JEE Main 2023 (January 29th Shift 2) Chemistry Question Paper with Answer Key

Uniform Acceleration - Definition, Equation, Examples, and FAQs

JEE Main 2023 (January 24th Shift 2) Chemistry Question Paper with Answer Key

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Displacement-Time Graph and Velocity-Time Graph for JEE

Atomic Structure - Electrons, Protons, Neutrons and Atomic Models

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

What is Hybridisation in Chemistry?

Other Pages
NCERT Solutions For Class 11 Physics Chapter 2 Motion In A Straight Line - 2025-26

NCERT Solutions For Class 11 Physics Chapter 1 Units and Measurements - 2025-26

NCERT Solutions For Class 11 Physics Chapter 3 Motion In A Plane - 2025-26

JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26

Motion in a Straight Line Class 11 Physics Chapter 2 CBSE Notes - 2025-26




