
What is produced in a rigid reflecting plane for displacement waves?
A) Beats
B) Node and antinode
C) Antinode
D) Node
Answer
179.7k+ views
Hint: When waves are propagating in the medium with time, it produces displacement on both sides of their direction of propagation. The maximum displacement of waves is called the amplitude. A vibrating rope tied toward one side will create a standing wave, the wave train, subsequent to showing up at the fixed finish of the rope, will be pondered back and superimposed itself as another train of waves in a similar plane. Due to obstruction between the two waves, the resultant abundance of the two waves will be the total of their individual amplitudes.
Complete step by step solution:
We present a figure of displacement wave in which consistently there are positions (N) along the rope, called nodes, at which there is no development by any means. There the two wave trains are consistently in resistance. On either side of a node is a vibrating antinode (A). The antinodes substitute toward uprooting with the goal that the rope at any moment takes after a diagram of the numerical capacity called the sine function.
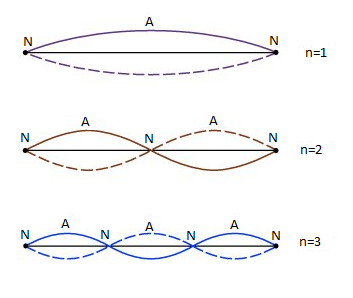
Hence it is clear that when a displacement wave incident at a rigid reflecting surface, makes Nodes and Antinodes. The mode of vibration in the waves depends on the number of nodes and antinodes formed.
Note: The best example of understanding of nodes and antinodes is open and closed organ pipes. Tied string is also an example of understanding nodes and antinodes. The expression of displacement/stationary wave in numeral form is –
\[y = 2a\cos( 2\pi x/\lambda) \sin (2\pi t/T)\]
Where \[x = \]displacement of wave in x-direction
\[\lambda = \] Wavelength of wave
\[t = \] Instant time
\[T = \] Time period of wave
Complete step by step solution:
We present a figure of displacement wave in which consistently there are positions (N) along the rope, called nodes, at which there is no development by any means. There the two wave trains are consistently in resistance. On either side of a node is a vibrating antinode (A). The antinodes substitute toward uprooting with the goal that the rope at any moment takes after a diagram of the numerical capacity called the sine function.

Hence it is clear that when a displacement wave incident at a rigid reflecting surface, makes Nodes and Antinodes. The mode of vibration in the waves depends on the number of nodes and antinodes formed.
Note: The best example of understanding of nodes and antinodes is open and closed organ pipes. Tied string is also an example of understanding nodes and antinodes. The expression of displacement/stationary wave in numeral form is –
\[y = 2a\cos( 2\pi x/\lambda) \sin (2\pi t/T)\]
Where \[x = \]displacement of wave in x-direction
\[\lambda = \] Wavelength of wave
\[t = \] Instant time
\[T = \] Time period of wave
Recently Updated Pages
Uniform Acceleration - Definition, Equation, Examples, and FAQs

JEE Atomic Structure and Chemical Bonding important Concepts and Tips

JEE Amino Acids and Peptides Important Concepts and Tips for Exam Preparation

JEE Electricity and Magnetism Important Concepts and Tips for Exam Preparation

Chemical Properties of Hydrogen - Important Concepts for JEE Exam Preparation

JEE Energetics Important Concepts and Tips for Exam Preparation

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Displacement-Time Graph and Velocity-Time Graph for JEE

Atomic Structure - Electrons, Protons, Neutrons and Atomic Models

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

What is Hybridisation in Chemistry?

Other Pages
NCERT Solutions For Class 11 Physics Chapter 2 Motion In A Straight Line - 2025-26

NCERT Solutions For Class 11 Physics Chapter 1 Units and Measurements - 2025-26

NCERT Solutions For Class 11 Physics Chapter 3 Motion In A Plane - 2025-26

JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26

Motion in a Straight Line Class 11 Physics Chapter 2 CBSE Notes - 2025-26




