




Superposition of Two SHMs: Formula, Cases & Applications
The Superposition Of SHM is a fundamental concept in oscillations and waves, crucial for scoring in JEE Main Physics. When two or more simple harmonic motions (SHMs) act simultaneously on the same particle, the resulting motion is found by algebraically adding their displacements. Superposition explains patterns like sound beats and Lissajous figures, making it both important theoretically and in practical applications. In musical instruments or tuning forks, the principle governs interference and resonance patterns, forming the basis for a wide range of JEE problems.
According to the superposition principle, if several SHMs of the same or different frequencies act on a system, the resulting displacement at any instant and position is simply the sum of the displacements due to each SHM individually. This is an application of the linearity of differential equations governing SHM, and holds only for linear systems.
Definition and Overview of Superposition Of SHM
In physics, the superposition of SHM refers to the addition of two or more simple harmonic motions acting on a single system. Each SHM can have its own amplitude, angular frequency, and phase. The principle is valid when the forces involved are linear, a condition fulfilled in ideal SHM systems. Superposition finds direct use in analyzing vibrations, sound waves, and is basic for topics like beats and resonance, which often appear in JEE exam questions.
Consider two SHMs along the same line:
y1 = A1sin(ωt + φ1)
and
y2 = A2sin(ωt + φ2)
The total displacement at any instant is:
y = y1 + y2 = A1sin(ωt + φ1) + A2sin(ωt + φ2)
General Formula for Superposition Of SHM
The general equation for the superposition of two SHMs with a common direction and frequency is:
| Motion Equation | Meaning |
|---|---|
| y = A1sin(ωt + φ1) + A2sin(ωt + φ2) | Sum of two SHMs (same direction) |
| y = R sin(ωt + θ) | Resultant SHM form |
| R = √[A12 + A22 + 2A1A2cos(φ1−φ2)] | Resultant amplitude |
| tanθ = (A1sinφ1 + A2sinφ2)/(A1cosφ1 + A2cosφ2) | Resultant phase |
This formula for resultant amplitude is frequently asked in exams. If the SHMs have equal amplitude and a phase difference φ, the resultant amplitude becomes 2Acos(φ/2).
When the frequencies differ slightly (ω1 ≈ ω2), the superposition leads to the phenomenon of beats, where the amplitude of the resultant oscillation varies periodically.
Superposition Of SHM: Same Line vs Perpendicular Directions
When two SHMs act along the same straight line (collinear), their direct sum gives another SHM with a new amplitude and phase, retaining the same frequency. However, when two independent SHMs act at right angles (perpendicular axes), the resulting motion traces various Lissajous figures whose shapes depend on frequency ratio and phase difference.
For SHMs at right angles:
x = A sin(ω1t + α)
y = B sin(ω2t + β)
- If ω1 = ω2 and β – α = 0: Straight line motion.
- If ω1 = ω2 and β – α = π/2: Ellipse or circle (A=B).
- If ω1 ≠ ω2: Complex Lissajous figures.
At equal frequencies but π/2 phase difference, the superposition results in uniform circular motion if the amplitudes are also equal. This graphical representation is important for interpreting oscilloscope traces and in musical tuning.
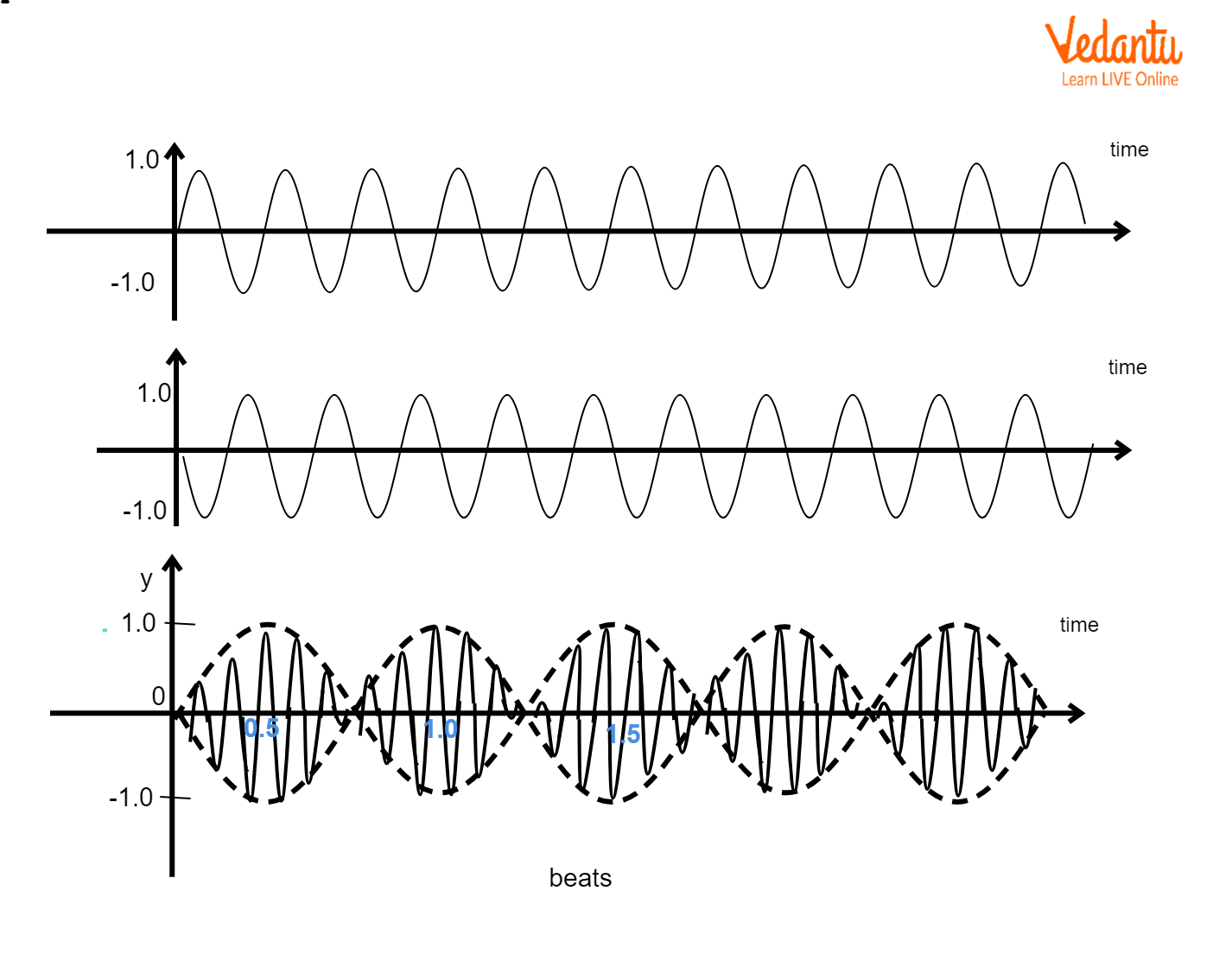
Beats and Superposition Of SHM
When two SHMs of nearly equal frequencies superpose along the same direction, periodic changes in loudness or intensity are observed—this is called beats. The condition for formation of beats is:
|f1 − f2| = Beat Frequency
If y1 = A sin(ω1t) and y2 = A sin(ω2t), the resultant can be written as:
| Resultant Motion | Interpretation |
|---|---|
| y = 2A cos[(Δω/2)t] sin[(ωavg)t] | Amplitude varies with cos[(Δω/2)t] |
Here, amplitude oscillates at beat frequency (Δf), causing alternating maxima and minima in intensity. Beats are commonly observed in instruments and tuning experiments, a favourite topic in JEE numericals.
Numerical Example: Superposition Of SHM in JEE
Example: Two SHMs, y1 = 3sin(ωt) cm and y2 = 4sin(ωt + π/2) cm, act along the same line.
- Resultant amplitude R = √[32 + 42 + 2 × 3 × 4 × cos(π/2)] = √[9+16] = 5 cm
- Resultant phase θ = tan−1[4/3] ≈ 53.13°
- Resultant motion: y = 5sin(ωt + 53.13°) cm
In JEE, always check phase difference and frequency before using resultant amplitude formulas. Also, unit consistency (cm, m, Hz) is essential to avoid errors.
Key Takeaways: Superposition Of SHM for JEE Main
- The resultant of two SHMs (same frequency, direction) is again a SHM.
- Resultant amplitude depends on phase difference: maximum when in phase, minimum (zero) if 180° out of phase.
- Beats form when frequencies differ slightly; beat frequency is |f1 − f2|.
- Perpendicular SHMs produce Lissajous figures like circles, ellipses, or more complex patterns.
- Master amplitude, phase formulas, and resultant interpretations for exam success.
| Case | Resultant |
|---|---|
| Same frequency, same direction | SHM with new amplitude, phase |
| Slight frequency difference | Beats (Amplitude varies periodically) |
| Perpendicular directions | Lissajous figures (shapes based on phase, frequency) |
For further exploration, review Simple Harmonic Motion and Principle of Superposition to deepen your concept clarity. See real examples in Beat Frequency Formula and Lissajous Figures for practical application. Superposition’s role in Sound Waves and Wave Motion is also often used in JEE analysis.
FAQs on Superposition of Simple Harmonic Motions: Complete Guide
1. What is the superposition of SHM?
Superposition of SHM refers to combining two or more simple harmonic motions to form a new resultant motion. This concept is important in physics for understanding phenomena such as beats, wave interference, and Lissajous figures.
- Found in topics like waves, oscillations, and acoustics
- The resultant motion depends on amplitudes, frequencies, and phase differences
- Applications occur in sound waves, mechanical waves, and physics experiments
2. What is the formula for the superposition of two simple harmonic motions?
The general formula for the superposition of two SHMs along the same line is:
y = A1sin(ωt + φ1) + A2sin(ωt + φ2)
- A1, A2: amplitudes of the individual SHMs
- ω: angular frequency (same or different)
- φ1, φ2: initial phases
- If ω1 = ω2, you can combine using the resultant amplitude and phase
3. When do beats form during the superposition of SHMs?
Beats form when two SHMs of slightly different frequencies are superposed, causing the amplitude of the resultant motion to periodically increase and decrease.
- Beat frequency = |f1 - f2|, where f1 and f2 are the frequencies of the two SHMs
- Beats are commonly observed in sound waves and tuning forks
4. How does superposition of SHM work in perpendicular directions?
When two SHMs of equal or different frequencies act at right angles, their superposition forms a pattern called a Lissajous figure.
- Equation: x = A1sin(ω1t + φ1), y = A2sin(ω2t + φ2)
- Pattern depends on the amplitude ratio, frequency ratio, and phase difference
- Used to visualize wave interference and in oscilloscope displays
5. What is the condition for two SHMs to produce stationary waves?
Stationary waves are produced when two SHMs of the same frequency, amplitude, and traveling in opposite directions superpose.
- Amplitudes must be nearly equal
- Frequencies and wavelengths must match
- Phase relationship must allow constructive and destructive interference
- This leads to the formation of nodes and antinodes in the medium
6. Can you give examples of superposition of SHMs in real life?
Yes, superposition of SHM occurs in many real-life situations, such as:
- Formation of beats when playing two similar musical notes
- Vibration patterns in bridges and buildings
- Interference of sound waves in auditoriums
- Lissajous patterns on cathode ray oscilloscopes in electronics
7. What happens when two SHMs of equal frequency but opposite phases superimpose?
When two SHMs of equal frequency and amplitude but phase difference of 180°, their resultant amplitude becomes zero, leading to complete destructive interference.
- Resultant displacement at all times is zero
- This is the condition for total cancellation
- Important in noise-cancelling applications and standing wave theory
8. What are common mistakes when combining SHMs with a phase difference?
Common errors when combining SHMs with phase difference include:
- Not using the correct vector addition formula for amplitudes
- Ignoring the effect of phase difference on resultant amplitude
- Forgetting to convert phase angles to radians if required
- Assuming resultant phase is always the average, which is incorrect
9. How do you calculate the resultant amplitude and phase when two SHMs combine?
To find the resultant amplitude (A) and phase (φ) when two SHMs of same frequency combine:
- Resultant amplitude: A = √[A1² + A2² + 2A1A2cos(Δφ)]
- Resultant phase: tanφ = (A1sinφ1 + A2sinφ2) / (A1cosφ1 + A2cosφ2)
- Where Δφ = φ2 - φ1
- Apply these for exam problems and waveform analysis
10. Why can't superposition occur in nonlinear systems?
Superposition only applies to linear systems, where responses add algebraically. In nonlinear systems:
- The output is not directly proportional to input
- Combining two solutions doesn't always yield another valid solution
- This means interference patterns and beats typical of SHMs won't form as expected
11. Do frequencies have to be exactly the same for superposition to occur?
Superposition can occur for any frequencies, but the resultant motion is simplest when frequencies are equal or very close.
- Equal frequencies yield simple harmonic or resultant motion with clear phase/amplitude sum
- Slightly different frequencies cause beats, a key sound wave phenomenon
- Very different frequencies combine to form complex, non-periodic signals
























