Question

If the vertices of a triangle area unit (2, −2), (−1, −1), and (5,2) then the equation of its circumcircle is?
A) \[\begin{array}{*{20}{c}}
  {{x^2} + {y^2} + 3x + 3y + 8}& = &0
\end{array}\]
B) \[\begin{array}{*{20}{c}}
  {{x^2} + {y^2} - 3x - 3y - 8}& = &0
\end{array}\]
C) \[\begin{array}{*{20}{c}}
  {{x^2} + {y^2} - 3x + 3y + 8}& = &0
\end{array}\]
D) None of these

Answer 1

Hint: First determine the center of the circumcircle and then find the radius of the circumcircle. After getting all these values, apply the equation of the circle.

Formula Used: \[\begin{array}{*{20}{c}}
  d& = &{\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} }
\end{array}\]

Complete step by step solution: In this problem, we have given that the vertices of the triangle are (2, −2), (−1, −1), and (5,2) respectively.
Let us assume that the center of the circumcircle is O \[\left( {{x_0},{y_0}} \right)\]and the radius of the circumcircle is R. Now, we will draw a figure according to the given data. Therefore,

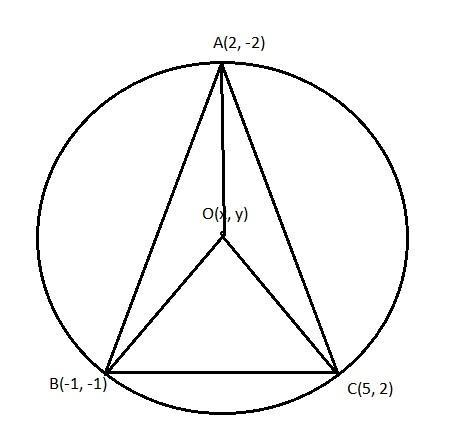
Figure 1
Now according to the figure that we have drawn,
\[ \Rightarrow OA = OB = OC = R\]
To determine the center of the circumcircle, we will write,
\[ \Rightarrow \begin{array}{*{20}{c}}
  {OA}& = &{OB}
\end{array}\] ………. (1)
And we know that the formula of the length of the line is,
\[ \Rightarrow \begin{array}{*{20}{c}}
  d& = &{\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} }
\end{array}\]
Therefore, The length of the OA,
\[ \Rightarrow \begin{array}{*{20}{c}}
  {OA}& = &{\sqrt {{{\left( {{x_0} - 2} \right)}^2} + {{\left( {{y_0} + 2} \right)}^2}} }
\end{array}\]
And OB will be,
\[ \Rightarrow \begin{array}{*{20}{c}}
  {OB}& = &{\sqrt {{{\left( {{x_0} + 1} \right)}^2} + {{\left( {{y_0} + 1} \right)}^2}} }
\end{array}\]
Now from equation (1). We will get
\[ \Rightarrow \begin{array}{*{20}{c}}
  {\sqrt {{{\left( {{x_0} - 2} \right)}^2} + {{\left( {{y_0} + 2} \right)}^2}} }& = &{\sqrt {{{\left( {{x_0} + 1} \right)}^2} + {{\left( {{y_0} + 1} \right)}^2}} }
\end{array}\]
Square both sides, we will get
\[ \Rightarrow \begin{array}{*{20}{c}}
  {{{\left( {{x_0} - 2} \right)}^2} + {{\left( {{y_0} + 2} \right)}^2}}& = &{{{\left( {{x_0} + 1} \right)}^2} + {{\left( {{y_0} + 1} \right)}^2}}
\end{array}\]
\[\begin{array}{*{20}{c}}
  { \Rightarrow 3{x_0} - {y_0}}& = &3
\end{array}\] …………. (A).
Similarly,
For OA and OC, so we will get
\[\begin{array}{*{20}{c}}
  { \Rightarrow OA}& = &{OC}
\end{array}\]
\[\begin{array}{*{20}{c}}
  { \Rightarrow \sqrt {{{\left( {{x_0} - 2} \right)}^2} + {{\left( {{y_0} + 2} \right)}^2}} }& = &{\sqrt {{{\left( {{x_0} - 5} \right)}^2} + {{\left( {{y_0} - 2} \right)}^2}} }
\end{array}\]
Square both sides we will get
\[\begin{array}{*{20}{c}}
  { \Rightarrow {{\left( {{x_0} - 2} \right)}^2} + {{\left( {{y_0} + 2} \right)}^2}}& = &{{{\left( {{x_0} - 5} \right)}^2} + {{\left( {{y_0} - 2} \right)}^2}}
\end{array}\]
\[\begin{array}{*{20}{c}}
  { \Rightarrow 6{x_1} + 8{y_1}}& = &{21}
\end{array}\] ……….. (B)
Now from the equation (A) and (B). we will get,
\[\begin{array}{*{20}{c}}
  { \Rightarrow {x_0}}& = &{\dfrac{3}{2}}
\end{array}\] and \[\begin{array}{*{20}{c}}
  {{y_0}}& = &{\dfrac{3}{2}}
\end{array}\]
Therefore, the coordinates of the center of the circumcircle are \[\left( {\dfrac{3}{2},\dfrac{3}{2}} \right)\]
Now we will determine the radius of the circumcircle. According to the figure we have,
\[ \Rightarrow OA = OB = OC = R\]
Now
\[\begin{array}{*{20}{c}}
  { \Rightarrow OA}& = &{\sqrt {{{\left( {\dfrac{3}{2} - 2} \right)}^2} + {{\left( {\dfrac{3}{2} + 2} \right)}^2}} }
\end{array}\]
\[\begin{array}{*{20}{c}}
  { \Rightarrow OA}& = &{\dfrac{5}{{\sqrt 2 }}}
\end{array}\]
Now apply the general equation of the circle, we will get
\[\begin{array}{*{20}{c}}
  { \Rightarrow {{\left( {x - {x_0}} \right)}^2} + {{\left( {y - {y_0}} \right)}^2}}& = &{{R^2}}
\end{array}\]
 Now put the values,
\[\begin{array}{*{20}{c}}
  { \Rightarrow {{\left( {x - \dfrac{3}{2}} \right)}^2} + {{\left( {y - \dfrac{3}{2}} \right)}^2}}& = &{{{\left( {\dfrac{5}{{\sqrt 2 }}} \right)}^2}}
\end{array}\]
\[\begin{array}{*{20}{c}}
  { \Rightarrow {x^2} + {y^2} - 3x - 3y - 8}& = &0
\end{array}\]

So, Option ‘B’ is correct

Note: It is important to note that the length of the lines OA, OB and OC will be equal (radii of the circle).