
Explain the formation of standing waves in case of an organ pipe open at one end and closed at the other end. Represent the first three modes of vibration diagrammatically and find their frequencies.
Answer
212.7k+ views
Hint: In this solution, we will use the relation of sound wave speed, distance, and velocity to determine the formation of standing waves and their frequencies. In a closed pipe, there is an antinode at the open end and a node at the closed end.
Complete step by step answer:
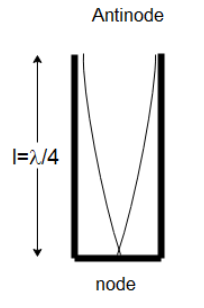
When sound waves are incident in a closed tube, they travel in the form of longitudinal waves. The waves that reach the closed bottom end of the tube, they are reflected back as shown in the diagrams below.
The closed wall of the tube acts as a rigid wall. This is because the air at the closed end is not free to vibrate. So, the reflected wave and the incident interfere with each other and form standing waves inside the organ. In this situation, a node is formed at the closed end. The air at the open end is free to vibrate with maximum amplitude and hence an antinode is formed there. This is the simplest mode of vibration of an air column in a closed well and is called the fundamental mode
We know that the velocity of a sound wave is the product of its frequency and wavelength i.e.
$v = f.\lambda $
In the standing mode, the wavelength of the wave must be such that
$n\lambda = 4L$ where $n$ is the order of the harmonic. For the fundamental harmonic, $n = 1$. And $L$ is the length of the pipe.
Using the above two relations, we can write
$\dfrac{{nv}}{f} = 4L$
$ \Rightarrow f = \dfrac{v}{{4L}}\,{\text{(for n = 1)}}$
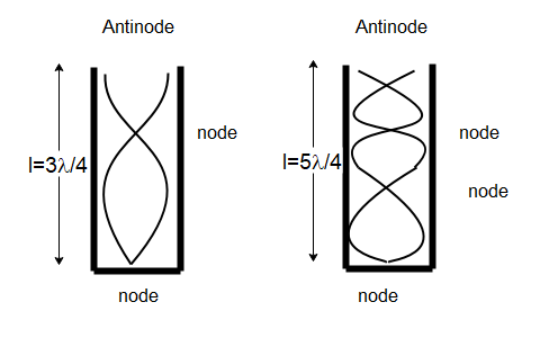
Now for a closed pipe, only antinodes can be formed at the open end of the pipe to form standing waves. So, only odd values of $n$ will be allowed to create standing waves as shown in the diagrams below.
So, the second overtone and the third overtone will have frequencies
${f_2} = \dfrac{{3v}}{{4l}}$
And
${f_3} = \dfrac{{5v}}{{4l}}$
The diagrams of the second and the third overtone respectively are shown below:
Note: While calculating the frequencies of the harmonic overtones, we must be careful that we select only odd values of \[n\]. This is because, for even values of $n$, an antinode will not be formed at the open end and standing waves won’t be able to form.
Complete step by step answer:
When sound waves are incident in a closed tube, they travel in the form of longitudinal waves. The waves that reach the closed bottom end of the tube, they are reflected back as shown in the diagrams below.
The closed wall of the tube acts as a rigid wall. This is because the air at the closed end is not free to vibrate. So, the reflected wave and the incident interfere with each other and form standing waves inside the organ. In this situation, a node is formed at the closed end. The air at the open end is free to vibrate with maximum amplitude and hence an antinode is formed there. This is the simplest mode of vibration of an air column in a closed well and is called the fundamental mode

We know that the velocity of a sound wave is the product of its frequency and wavelength i.e.
$v = f.\lambda $
In the standing mode, the wavelength of the wave must be such that
$n\lambda = 4L$ where $n$ is the order of the harmonic. For the fundamental harmonic, $n = 1$. And $L$ is the length of the pipe.
Using the above two relations, we can write
$\dfrac{{nv}}{f} = 4L$
$ \Rightarrow f = \dfrac{v}{{4L}}\,{\text{(for n = 1)}}$
Now for a closed pipe, only antinodes can be formed at the open end of the pipe to form standing waves. So, only odd values of $n$ will be allowed to create standing waves as shown in the diagrams below.
So, the second overtone and the third overtone will have frequencies
${f_2} = \dfrac{{3v}}{{4l}}$
And
${f_3} = \dfrac{{5v}}{{4l}}$
The diagrams of the second and the third overtone respectively are shown below:

Note: While calculating the frequencies of the harmonic overtones, we must be careful that we select only odd values of \[n\]. This is because, for even values of $n$, an antinode will not be formed at the open end and standing waves won’t be able to form.
Recently Updated Pages
JEE Main Colleges 2026 List: Admission Details for NITs, IIITs, GFTIs

Uniform Acceleration: Definition, Equations & Graphs for JEE/NEET

Mass vs Weight: Key Differences, Units & Examples Explained

JEE Electricity and Magnetism Important Concepts and Tips for Exam Preparation

JEE Energetics Important Concepts and Tips for Exam Preparation

JEE Isolation, Preparation and Properties of Non-metals Important Concepts and Tips for Exam Preparation

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

JEE Main Correction Window 2026 Session 1 Dates Announced - Edit Form Details, Dates and Link

Equation of Trajectory in Projectile Motion: Derivation & Proof

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

Hybridisation in Chemistry – Concept, Types & Applications

Angle of Deviation in a Prism – Formula, Diagram & Applications

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26

NCERT Solutions For Class 11 Physics Chapter 8 Mechanical Properties Of Solids

Motion in a Straight Line Class 11 Physics Chapter 2 CBSE Notes - 2025-26

NCERT Solutions for Class 11 Physics Chapter 7 Gravitation 2025-26

Collision: Meaning, Types & Examples in Physics




