
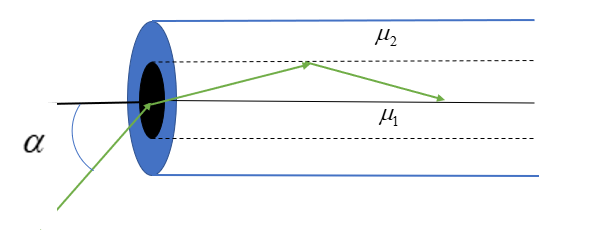
An optical fiber consists of core of ${\mu _1}$ surrounded by a cladding of ${\mu _2} < {\mu _1}$ A beam of light enters from air at an angle α with axis of fiber. The highest α for which ray can be traveled through fiber is
A. ${\cos ^{ - 1}}\sqrt {{\mu ^2}_1 - {\mu ^2}_2} $
B. ${\sin ^{ - 1}}\sqrt {{\mu ^2}_1 - {\mu ^2}_2} $
C. ${\sec ^{ - 1}}\sqrt {{\mu ^2}_1 - {\mu ^2}_2} $
D. ${\tan ^{ - 1}}\sqrt {{\mu ^2}_1 - {\mu ^2}_2} $
Answer
180k+ views
Hint: In this question we will be using the snell's law and basic trigonometric identities to solve and get the desired answer. When light travels from one medium to another, Snell's law is used to link the angle of incidence and angle of reflection with the refractive index of a medium.
Formula used:
$\dfrac{{\sin \alpha }}{{\sin r}} = {\mu _1}$
Complete step by step solution:
Refraction is the study of how light bends when it comes into contact with two media that have different refractive indices. As a result, the refractive indices of the two media may be related through the angle associated with incidence and refraction.
Snell’s law: The reciprocal of the ratio of the indices of refraction, or the ratio of phase velocities in the two media, is said to be identical to the ratio of the sines of the angles of incidence and refraction.
$\dfrac{{\sin \alpha }}{{\sin r}} = {\mu _1}$ --------- (1)
Where ${\mu _1} = $refractive index of medium 1,
$\alpha$ is angle of incident
$r$ is the angle of refraction
So that TIR take place at core and cladding interface
$90 - {\theta _c} > r$ where $\sin {\theta _c} = \dfrac{{{\mu _2}}}{{{\mu _1}}}$
$ \Rightarrow \sin (90 - {\theta _c}) > \sin r$ ------ (2)
Also using equation 1 we get
$\sin \alpha = {\mu _1}\sin r$ ---------(3)
So, from equation 2 and 3 we get
$\cos {\theta _c} > \dfrac{{\sin \alpha }}{{{\mu _1}}}$
Also, we know that $\cos {\theta _c} = \sqrt {1 - {{\sin }^2}{\theta _c}} $
From 1st equation $\cos {\theta _c} = \sqrt {1 - \dfrac{{{\mu ^2}_2}}{{{\mu ^2}_1}}} $
$ \Rightarrow \sin \alpha < {\mu _1}\sqrt {1 - \dfrac{{{\mu ^2}_2}}{{{\mu ^2}_1}}} $
\[ \Rightarrow \sin \alpha < \sqrt {{\mu ^2}_1 - {\mu ^2}_2} \]
$\therefore {\alpha _{\max }} = {\sin ^{ - 1}}\sqrt {{\mu ^2}_1 - {\mu ^2}_2} $
Hence option B is correct.
Note: Refraction only occurs when light rays go from a denser to a less common medium. This is due to the fact that total internal refraction cannot occur when light rays move from a rarer to a denser medium since the refracted angle is always smaller than the incident angle. Since the angle of incidence can never be more than 90 degrees, neither can the angle of refraction.
Formula used:
$\dfrac{{\sin \alpha }}{{\sin r}} = {\mu _1}$
Complete step by step solution:
Refraction is the study of how light bends when it comes into contact with two media that have different refractive indices. As a result, the refractive indices of the two media may be related through the angle associated with incidence and refraction.
Snell’s law: The reciprocal of the ratio of the indices of refraction, or the ratio of phase velocities in the two media, is said to be identical to the ratio of the sines of the angles of incidence and refraction.
$\dfrac{{\sin \alpha }}{{\sin r}} = {\mu _1}$ --------- (1)
Where ${\mu _1} = $refractive index of medium 1,
$\alpha$ is angle of incident
$r$ is the angle of refraction
So that TIR take place at core and cladding interface
$90 - {\theta _c} > r$ where $\sin {\theta _c} = \dfrac{{{\mu _2}}}{{{\mu _1}}}$
$ \Rightarrow \sin (90 - {\theta _c}) > \sin r$ ------ (2)
Also using equation 1 we get
$\sin \alpha = {\mu _1}\sin r$ ---------(3)
So, from equation 2 and 3 we get
$\cos {\theta _c} > \dfrac{{\sin \alpha }}{{{\mu _1}}}$
Also, we know that $\cos {\theta _c} = \sqrt {1 - {{\sin }^2}{\theta _c}} $
From 1st equation $\cos {\theta _c} = \sqrt {1 - \dfrac{{{\mu ^2}_2}}{{{\mu ^2}_1}}} $
$ \Rightarrow \sin \alpha < {\mu _1}\sqrt {1 - \dfrac{{{\mu ^2}_2}}{{{\mu ^2}_1}}} $
\[ \Rightarrow \sin \alpha < \sqrt {{\mu ^2}_1 - {\mu ^2}_2} \]
$\therefore {\alpha _{\max }} = {\sin ^{ - 1}}\sqrt {{\mu ^2}_1 - {\mu ^2}_2} $
Hence option B is correct.
Note: Refraction only occurs when light rays go from a denser to a less common medium. This is due to the fact that total internal refraction cannot occur when light rays move from a rarer to a denser medium since the refracted angle is always smaller than the incident angle. Since the angle of incidence can never be more than 90 degrees, neither can the angle of refraction.
Recently Updated Pages
Chain and Position Isomerism Important Concepts and Tips for JEE

JEE Main 2021 July 20 Shift 2 Question Paper with Answer Key

Froth Flotation Principle and Process Important Concepts and Tips for JEE

JEE Main 2022 (June 27th Shift 2) Physics Question Paper with Answer Key

Covalent Character in Ionic Compounds Important Concepts for JEE

JEE Habers Process for Manufacture of Ammonia Important Concepts and Tips

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Displacement-Time Graph and Velocity-Time Graph for JEE

Electric field due to uniformly charged sphere class 12 physics JEE_Main

Atomic Structure - Electrons, Protons, Neutrons and Atomic Models

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

What is Hybridisation in Chemistry?

JEE Main 2025: Conversion of Galvanometer Into Ammeter And Voltmeter in Physics

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

Wheatstone Bridge for JEE Main Physics 2025

Electric Field Due to Uniformly Charged Ring for JEE Main 2025 - Formula and Derivation




